优化算法

1 小批量梯度下降（Mini-batch gradient descent）

1.1 什么是小批量下降算法

机器学习是一个高度依赖经验的不断重复的过程，需要训练很多模型才能找到一个最好用的。快速的优化算法、好的优化算法能够大幅提高我们的效率。

矢量化(vectorization)运算能够有效地一次性计算所有 m 个样本，而不是用一个具体的 for 循环来处理整个训练集。传统的梯度下降算法很好的利用了矢量化运算，但是 m 越大，参数更新就越慢。为了解决这个问题，可以这样做：

• 首先将你的训练集拆分成多个小型训练集，即小批量(mini_batch)，比如说每一个小型训练集只有 64 个训练样本；
• 每处理一个 mini_batch 后就更新一次参数。

而这中方法被叫做小批量下降算法（MBGD）。

第 i 个小批量样本集可表示为 ($X^{\{t\}},Y^{\{t\}}$) ，在小批量梯度下降中，对整个训练集，也就是所有 mini_batch 的一次遍历叫做一个 epoch。

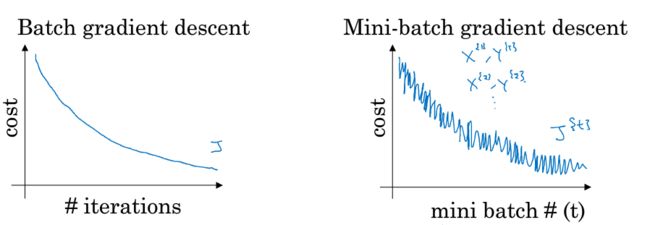
在梯度下降算法中 ，每一次迭代需要遍历整个训练集，对于迭代次数来说，代价函数 J 通常是单调递减的。
而在小批量梯度下降中，每次迭代都是使用不同的训练集，也就是使用不同的小块 (mini-batch) ，所以代价函数 J 并不一定每次迭代都会下降，它是一个振荡的曲线但是整体趋势必须是向下的。

1.2 如何设置batch的大小

先来看看两种极端的情况：

（1）当 batch = 训练样本总数 时，此时小批量梯度下降算法就相当于批量梯度下降（BGD），即普通的梯度下降算法。
优点： 一次处理整个训练集，从而能更准确地朝总体损失最小的方向移动。当目标函数为凸函数时，BGD一定能够得到全局最优
缺点： 当数据集很大时，一次处理整个训练集，计算量大，参数更新也就慢。所以普通梯度下降算法适合与数据集比较小的时候。

（2）当 batch = 1 时，此时小批量梯度下降算法就成了 随机梯度下降算法（SGD）。
优点： 每处理完一个样本就更新参数，从而参数更新的速度大大加快。
缺点： 一个样本不能反映出总体样本的误差，所以其准确性可能不如普通梯度下降算法高；可能会走很多弯路，出现徘徊现象；可能会收敛到局部最优，即使代价函数为强凸函数的情况下，此方法仍可能无法做到线性收敛。

而小批量梯度下降算法（MBGD），batch的取值则是介于 1 到训练样本总数之间，中和了批量梯度下降算法与随机梯度下降算法的优缺点。

在小批量梯度下降算法（MBGD）中，batch 一般取值为 2 的整数次幂，例如：16、32、64、128、256等。

(1）增大 batch 的影响：
       a. 矢量化运算效率提高，但参数更新速度降低。
       b.梯度下降的方向的准确度增高，震荡现象减少，收敛到全局最优的可能性增加。

(2）减小 batch 的影响：
       a. 不能充分利用矢量化计算，但更新参数的速度提高。
       b.梯度下降的方向的准确度降低。会出现震荡，收敛到局部最优的可能性增加。

2 指数加权平均

2.1 指数加权平均定义与步骤

指数加权平均（exponentially weighted averges）：
       在统计学上也被称为指数加权滑动平均，是指应用指数级降低的加权因子，使得较旧数据的权重都呈指数下降，但不会等于零。

求解步骤：
       初始化：$v_0=0$
       求平均值：$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$
其中 β 为参数（取值介于 0 到 1 之间），$v_0$ 为初始平均值，$v_t$ 为前 $t$ 为条记录的平均值，${\theta }_t$ 为第 $t$ 条记录实际值。

以伦敦某年365天的温度作为例，如下图，左边是对每天实际温度的记录，右边是对应的散点图。

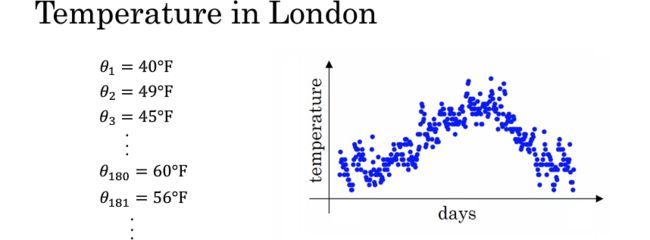
这些数据看起来好像有些噪声。如果想要计算数据的趋势，即温度的局部平均或滑动平均，可以用指数加权平均法。具体步骤如下图左，我们用 $v_t$ 代表前 $t$ 天的指数加权平均温度，结果用红色画出来，就会得到图右的红色曲线，称为每日温度的指数加权平均。

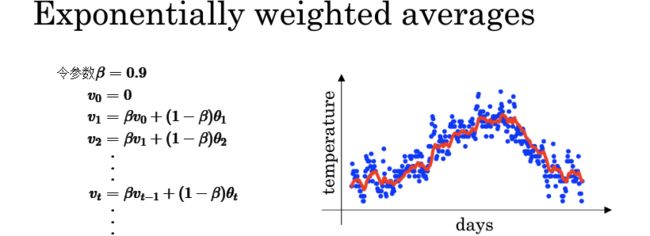
那么为什么叫指数加权平均呢？通过其公式层层代入，可以得到：$$v_t=(1-\beta ){\theta }_t+(1-\beta )\beta {\theta }_{t-1}+(1-\beta ){\beta }^2{\theta }_{t-2}+...+(1-\beta ){\beta }^{t-1}{\theta }_1=\frac{1}{1/(1-\beta )}\sum _{i=0}^{t-1}{\beta }^i{\theta }_{t-i}$$其中 ${\beta }^i$ 介于 0 到 1 之间，相当于记录实际值 ${\theta }_{t-i}$的权值，而这个权值又是呈指数减小的。 $\frac{1}{1-\beta }$ 则可以看作是对最近 $\frac{1}{1-\beta }$ 天的记录求平均值，所以这就是“指数加权平均”这个名字的由来。

2.2 参数 beta 的取值

其中参数 $\beta$ 的值可以调整，可以认为 $v_t$ 近似于 $\frac{1}{1-\beta }$ 天温度的平均。

$\beta$ 的取值越大，得到的曲线会更平滑，因为你对更多天数的温度做了平均处理，因此曲线就波动更小。另一方面，这个曲线会右移，因为计算平均温度的天数增加，这个指数加权平均的公式在温度变化时，适应得更加缓慢，这就造成了一些延迟。

$\beta$ 的取值越小，得到结果中会有更多的噪声，得到的曲线振荡现象就会越明显。但它可以更快地适应温度变化。

通过调整这个参数 $\beta$，就可以得到略微不同的效果。上图展示了 $\beta$ 取两个极端值（0.5 和 0.98）和一个中间值（0.9）的指数加权平均结果曲线。通常 $\beta$ 取中间的某个值效果最好，也就是这里的红色曲线，它对温度的平均比绿色或者黄色的曲线更好，因为它在平滑去噪的基础上更好的刻画了温度的变化趋势。

2.3 偏差修正（Bias correction）

当我们对一组数据进行指数加权平均运算时，在刚开始的几次运算得出的结果比实际值要小，随着参与计算的平均值的实际记录值越来越多，算出来的平均值也就越来越准确了。如果我们希望在开始的时候得到比较正确的平均值，那么可以利用偏差修正（Bias correction）技术，步骤如下：

1. 求指数加权平均值：$v_t=\beta v_{t-1}+(1-\beta ){\theta }_t$
2. 执行偏差修正：$v_t=\frac{v_t}{1-{\beta }^t}$

可以看到，当 $t$ 值足够大时，分母 $1-{\beta }^t$ 是趋向于 1 的，所以偏差修正值对结果将基本没有影响。也就是说在后期偏差修正发挥的作用就越来越小了。

在机器学习中，很多的指数加权平均运算，并不会使用偏差修正，因为大多数人更愿意在初始阶段用一个稍带偏差的值进行运算。不过，如果在初始阶段就开始考虑偏差，偏差修正可以帮我们尽早做出更好的估计。

3 三个有效的优化算法

3.1 动量梯度下降算法（Gradient descent with momentum）

在训练过程中，梯度下降算法会计算很多步，并且在朝着代价最低点靠近的过程中会伴随着上下波动（振荡），如下图蓝色轨迹所示。这种振荡会减慢梯度下降的速度，同时也让我们无法使用较大的学习率。学习率越大，振荡的幅度也就越大，严重时可能会像下图紫色轨迹那样发散出去。

为了加速梯度下降的进程，且能够使用较大的学习率，我们可以对反向传播得到的梯度进行指数加权平均运算，从而
减少梯度下降过程中的振荡，使梯度下降轨迹更加平滑。具体做法为：

初始化：
       $V_{dW}$ 初始化为与 $dW$ 形状相同的全零矩阵
       $V_{db}$ 初始化为与 $db$ 形状相同的全零矩阵
在第 $t$ 次迭代中：
       $V_{dW}={\beta }_1{V}_{dW}+(1-{\beta }_1)dW$
       $V_{db}={\beta }_1{V}_{db}+(1-{\beta }_1)db$
       $W=W-\alpha V_{dW}$
       $b=b-\alpha V_{db}$
这里 ${\beta }_1$ 通常取值为 0.9

3.2 均方根传递 RMSprop (Root Mean Square prop)

与动量梯度下降算法类似，它也可以加速梯度下降。步骤如下：

初始化：
       $S_{dW}$ 初始化为与 $dW$ 形状相同的全零矩阵
       $S_{db}$ 初始化为与 $db$ 形状相同的全零矩阵
在第 $t$ 次迭代中：
       $S_{dW}={\beta }_2{S}_{dW}+(1-{\beta }_2)(dW{)}^2$
       $S_{db}={\beta }_2{S}_{db}+(1-{\beta }_2)(db{)}^2$
       $W=W-\alpha \frac{dW}{\sqrt{S_{dW}+ϵ}}$
       $b=b-\alpha \frac{db}{\sqrt{S_{db}+ϵ}}$
这里 ${\beta }_2$ 通常取值为 0.999，$ϵ$ 通常取值为 $10^{-8}$

其中 $ϵ$ 的存在是为了防止 $S_{dW}$ 或 $S_{db}$ 为零时导致分母为零。

3.3 Adam优化算法（Adaptive Moment Estimation）

Adam算法将动量梯度下降算法与均方根传递算法结合在了一起，是一种极其重用的优化算法，被证明能有效适用于不同的神经网络和广泛的结构。具体步骤如下：

初始化：
       $V_{dW}$、$S_{dW}$初始化为与$dW$ 形状相同的全零矩阵
       $V_{db}$、$S_{db}$初始化为与 $db$形状相同的全零矩阵


在第 $t$ 次迭代中：

       $V_{dW}={\beta }_1{V}_{dW}+(1-{\beta }_1)dW$

       $V_{db}={\beta }_1{V}_{db}+(1-{\beta }_1)db$

       $S_{dW}={\beta }_2{S}_{dW}+(1-{\beta }_2)(dW{)}^2$

       $S_{db}={\beta }_2{S}_{db}+(1-{\beta }_2)(db{)}^2$

       $V_{dW}^{corrected}=\frac{V_{dW}}{1-({\beta }_1{)}^t}$

       $V_{db}^{corrected}=\frac{V_{db}}{1-({\beta }_1{)}^t}$

       $S_{dW}^{corrected}=\frac{S_{dW}}{1-({\beta }_1{)}^t}$

       $S_{db}^{corrected}=\frac{S_{db}}{1-({\beta }_1{)}^t}$

       $W=W-\alpha \frac{V_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}+ϵ}}$

       $b=b-\alpha \frac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}+ϵ}}$

这里 ${\beta }_1$ 通常取值为 0.9，${\beta }_2$ 通常取值为 0.999，$ϵ$ 通常取值为$10^{-8}$

4 学习率衰减(Learning rate decay)

当进行小批量梯度下降时，迭代过程中步长(steps)会有些振荡，它会逐步靠近代价最小值点并周围摆动，但不会完全收敛到这一点。因为你的学习率 α 取了固定值，且不同的批次也可能产生些噪声。此时得到的梯度下降曲线如下图蓝线所示。

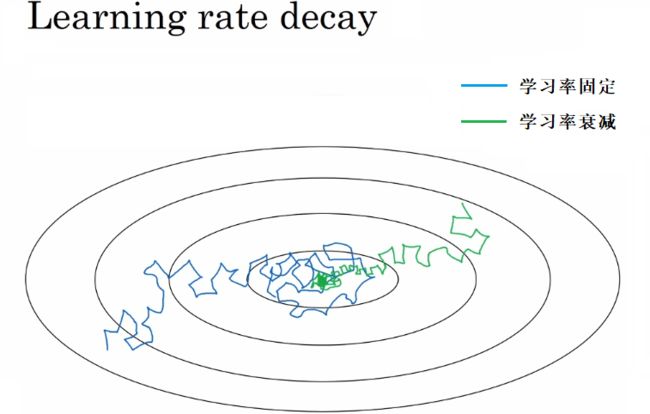
但是我们让学习率 α 逐步衰减，那么在初始阶段，因为学习率α取值还比较大，学习速度仍然可以比较快，但随着学习率降低 α变小，步长也会渐渐变小，所以最终将围绕着离极小值点更近的区域摆动，即使继续训练下去也不会漂游远离。此时得到的梯度下降曲线如上图绿线所示。

那么如何实现在迭代中实现率衰减(learning rate decay)呢？方法有很多：

1. $\alpha =\frac{1}{1+decay\_rate\ast epoch\_num}{\alpha }_0$
2. $\alpha =0.95^{epoch\_num}{\alpha }_0$
3. $\alpha =\frac{k}{\sqrt{epoch\_num}}{\alpha }_0$ 或者 $\alpha =\frac{k}{\sqrt{batch\_num}}{\alpha }_0$
4. 根据训练情况手动调整
   
   
   

5 局部最优与鞍点、停滞区

5.1 局部最优（Local Optima）与鞍点（Saddle Point）

对于梯度下降或其他的算法，都很容易陷入局部最优（Local Optima） 而找不到全局最优。

在二维平面中，确实很容易存在很多局部最优。但实际上，如果你是在训练一个神经网络，参数 w 不止一个，代价函数中大部分梯度为零的点实际上并不是局部最优，而是鞍点（Saddle Point） 。在鞍点附近，代价函数 J 对于某些 w 是凸函数，而对另外一些 w 是凹函数。而局部最优或全局最优则要求代价函数 J 在任意一个方向上都是凸函数。

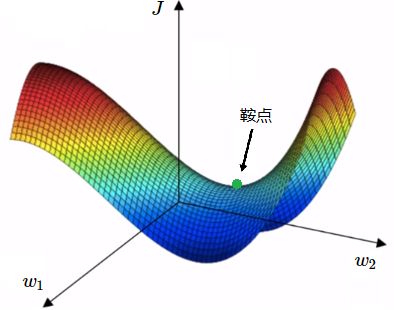
我们在低维空间里的大部分直观感受，实际上并不适用于深度学习算法所应用高维空间。对于一个高维空间的函数，如果某点处梯度为零，则在每个方向上可能是凸函数，或者是凹函数。假设在一个 20000 维的空间中，如果一个点要成为局部最优，则需要在所有的 20000 个方向上都是凸函数。因此这件事发生的概率非常低，大概为 $0.5^{20000}$，所以你更有可能遇到的情况是鞍点，而不是局部最优。

也就是说，如果训练的是一个较大的神经网络，有很多参数，代价函数 J 定义在一个相对高维的空间上，实际上不太可能陷入糟糕的局部最优。

5.2 停滞区（Plateaus）

实际上，真正会降低学习速度的实际上是停滞区（Plateaus）。停滞区指的是导数长时间接近于零的一段区域。

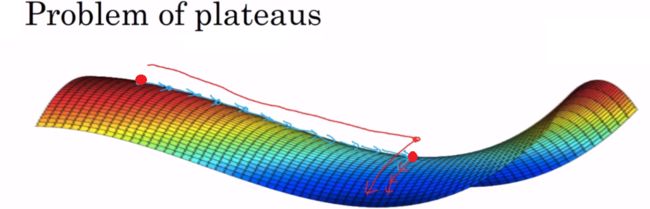
从左上角的红点开始，那么梯度下降会沿着这个曲面向下移动。然而因为梯度为零或接近于零，曲面很平，梯度下降会花费很长的时间，缓慢地找到停滞区里的红点（中间的红点）。然后因为左侧或右侧的随机扰动，才终于能够离开这个停滞区。

也就是说，停滞区会让学习过程变得相当慢，这也是动量（Momentum）算法、RmsProp 算法或 Adam 算法能改善学习算法的地方。