AOE网与关键路径
- AOE网
- 关键路径
- 求关键路径的算法实现
AOE网是以边表示活动的有向无环网,在AOE网中,具有最大路径长度的路径称为关键路径,关键路径表示完成工程的最短工期。
1.AOE网
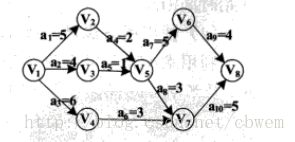
AOE网是一个带权的有向无环图。其中用顶点表示事件,弧表示活动,权值表示两个活动持续的时间。AOE网是以边表示活动的网。
AOV网描述了活动之间的优先关系,可以认为是一个定性的研究,但是有时还需要定量地研究工程的进度,如整个工程的最短完成时间、各个子工程影响整个工程的程度、每个子工程的最短完成时间和最长完成时间。在AOE网中,通过研究事件和活动之间的关系,可以确定整个工程的最短完成时间,明确活动之间的相互影响,确保整个工程的顺利进行。
在用AOE网表示一个工程计划时,用顶点表示各个事件,弧表示子工程的活动,权值表示子工程的活动需要的时间。在顶点表示事件发生之后,从该顶点出发的有向弧所表示的活动才能开始。在进入某个顶点的有向弧所表示的活动完成之后,该顶点表示的事件才能发生。
对一个工程来说,只有一个开始状态和一个结束状态。因此在AOE网中,只有一个入度为零的点表示工程的开始,称为源点;只有一个出度为零的点表示工程的结束,称为汇点。
2.关键路径
关键路径是指在AOE网中从源点到汇点路径最长的路径。这里的路径长度是指路径上各个活动持续时间之和。在AOE网中,有些活动是可以并行执行的,关键路径其实就是完成工程的最短时间所经过的路径。关键路径上的活动称为关键活动。
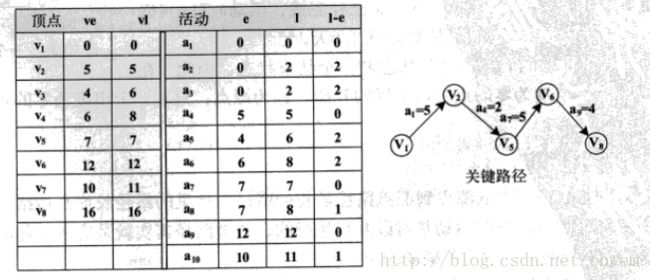
1. 事件vivi的最早发生时间:从源点到顶点vivi的最长路径长度,称为事件vivi的最早发生时间,记作ve(i)。求解ve(i)可以从源点ve(0)=0开始,按照拓扑排序规则根据递推得到:
ve(i)=Max{ve(k)+dut(
其中T是所有以第i个顶点为弧头的弧的集合,dut(
2. 事件vivi的最晚发生时间:在保证整个工程完成的前提下,活动最迟的开始时间,记作vl(i)。z 求解vivi的最早发生时间ve(i)的前提vl(n-1)=ve(n-1)下,从汇点开始,向源点推进得到:
vl(i)=Min{vl(k)−dut(
其中S是所有以第i个顶点为弧尾的弧的集合,dut(
3.活动aiai的最早开始时间e(i):如果弧
4.活动aiai的最晚开始时间l(i):在不推迟整个工程完成时间的基础上,活动aiai最迟必须开始的事件。如果弧
5.活动aiai的松弛时间:活动aiai的最晚开始时间域最早开始时间之差就是活动aiai的松弛时间,记作l(i)-e(i)。
当e(i)=l(i)时,对应的活动aiai称为关键活动,非关键活动提前完成或推迟完成并不会影响到整个工程的进度。
求AOE网的关键路径的算法:
1. 对AOE网中的顶点进行拓扑排序,如果得到的拓扑序列顶点个数小于网中顶点数,则说明网中有环存在,不能求关键路径,终止算法。否则,从源点v0v0开始,求出各个顶点的最早发生时间ve(i)。
2. 从汇点vnvn出发vl(n-1)=ve(n-1),按照逆拓扑序列求其他顶点的最晚发生时间vl(i)。
3. 由各顶点的最早发生时间ve(i)和最晚发生时间vl(i),求出每个活动aiai的最早开始时间e(i)和最晚开始时间l(i)。
4. 找出所有满足条件e(i)=l(i)的活动aiai,aiai即是关键活动。
关键路径经过的顶点是满足条件ve(i)==vl(i),即当事件的最早发生时间与最晚发生时间相等时,该顶点一定在关键路径之上。同样,关键活动者的弧满足条件e(i)=l(i),即当活动的最早开始时间域最晚开始时间相等时,该活动一定是关键活动。因此,要求关键路径,需要首先求出网中每个顶点的对应事件的最早开始时间,然后推出事件的最晚开始时间和活动的最早、最晚开始时间,最后再判断顶点是否在关键路径之上,得到网的关键路径。
要求每一个顶点的最早开始时间,首先要将网中的顶点进行拓扑排序。在对顶点进行拓扑排序的过程中,同时计算顶点的最早发生时间ve(i)。从源点开始,由与源点相关联的弧的权值,可以得到该弧相关联顶点对应事件的最早发生时间。同时定义一个栈T,保存顶点的逆拓扑序列。
3.求关键路径的算法实现
采用邻接表创建上图所示的有向网,并求网中顶点的拓扑序列,然后计算该有向网的关键路径。
- 头文件栈
#define StackSize 100
typedef struct
{
DataType stack[StackSize];
int top;
}SeqStack;
void InitStack(SeqStack *S)
/*将栈初始化为空栈只需要把栈顶指针top置为0*/
{
S->top=0; /*把栈顶指针置为0*/
}
int StackEmpty(SeqStack S)
/*判断栈是否为空,栈为空返回1,否则返回0*/
{
if(S.top==0) /*判断栈顶指针top是否为0*/
return 1; /*当栈为空时,返回1;否则返回0*/
else
return 0;
}
int GetTop(SeqStack S, DataType *e)
/*取栈顶元素。将栈顶元素值返回给e,并返回1表示成功;否则返回0表示失败。*/
{
if(S.top<=0) /*在取栈顶元素之前,判断栈是否为空*/
{
printf("栈已经空!\n");
return 0;
}
else
{
*e=S.stack[S.top-1]; /*在取栈顶元素*/
return 1;
}
}
int PushStack(SeqStack *S,DataType e)
/*将元素e进栈,元素进栈成功返回1,否则返回0.*/
{
if(S->top>=StackSize) /*在元素进栈前,判断是否栈已经满*/
{
printf("栈已满,不能进栈!\n");
return 0;
}
else
{
S->stack[S->top]=e; /*元素e进栈*/
S->top++; /*修改栈顶指针*/
return 1;
}
}
int PopStack(SeqStack *S,DataType *e)
/*出栈操作。将栈顶元素出栈,并将其赋值给e。出栈成功返回1,否则返回0*/
{
if(S->top<=0) /*元素出栈之前,判断栈是否为空*/
{
printf("栈已经没有元素,不能出栈!\n");
return 0;
}
else
{
S->top--; /*先修改栈顶指针,即出栈*/
*e=S->stack[S->top]; /*将出栈元素赋值给e*/
return 1;
}
}
int StackLength(SeqStack S)
/*求栈的长度,即栈中元素个数,栈顶指针的值就等于栈中元素的个数*/
{
return S.top;
}
void ClearStack(SeqStack *S)
/*将栈初始化为空栈只需要把栈顶指针top置为0*/
{
S->top=0; /*把栈顶指针置为0*/
}- 类型定义
#include
#include
#include
#include
typedef int DataType; /*栈元素类型定义*/
#include"SeqStack.h"
/*图的邻接表类型定义*/
typedef char VertexType[4];
typedef int InfoPtr; /*定义为整型,为了存放权值*/
typedef int VRType;
#define MaxSize 50 /*最大顶点个数*/
typedef enum{DG,DN,UG,UN}GraphKind; /*图的类型:有向图、有向网、无向图和无向网*/
typedef struct ArcNode /*边结点的类型定义*/
{
int adjvex; /*弧指向的顶点的位置*/
InfoPtr *info; /*弧的权值*/
struct ArcNode *nextarc; /*指示下一个与该顶点相邻接的顶点*/
}ArcNode;
typedef struct VNode /*头结点的类型定义*/
{
VertexType data; /*用于存储顶点*/
ArcNode *firstarc; /*指示第一个与该顶点邻接的顶点*/
}VNode,AdjList[MaxSize];
typedef struct /*图的类型定义*/
{
AdjList vertex;
int vexnum,arcnum; /*图的顶点数目与弧的数目*/
GraphKind kind; /*图的类型*/
}AdjGraph; - 有向网的拓扑排序
int ve[MaxSize]; /*ve存放事件最早发生时间*/
int TopologicalOrder(AdjGraph N,SeqStack *T)
/*采用邻接表存储结构的有向网N的拓扑排序,并求各顶点对应事件的最早发生时间ve*/
/*如果N无回路,则用用栈T返回N的一个拓扑序列,并返回1,否则为0*/
{
int i,k,count=0;
int indegree[MaxSize]; /*数组indegree存储各顶点的入度*/
SeqStack S;
ArcNode *p;
/*将图中各顶点的入度保存在数组indegree中*/
for(i=0;iadjvex;
indegree[k]++;
p=p->nextarc;
}
}
InitStack(&S); /*初始化栈S*/
printf("拓扑序列:");
for(i=0;inextarc) /*处理编号为i的顶点的每个邻接点*/
{
k=p->adjvex; /*顶点序号为k*/
if(--indegree[k]==0) /*如果k的入度减1后变为0,则将k入栈S*/
PushStack(&S,k);
if(ve[i]+*(p->info)>ve[k]) /*计算顶点k对应的事件的最早发生时间*/
ve[k]=ve[i]+*(p->info);
}
}
if(count - 有向网的关键路径
int CriticalPath(AdjGraph N)
/*输出N的关键路径*/
{
int vl[MaxSize]; /*事件最晚发生时间*/
SeqStack T;
int i,j,k,e,l,dut,value,count,e1[MaxSize],e2[MaxSize];
ArcNode *p;
if(!TopologicalOrder(N,&T)) /*如果有环存在,则返回0*/
return 0;
value=ve[0];
for(i=1;ivalue)
value=ve[i]; /*value为事件的最早发生时间的最大值*/
for(i=0;inextarc)
/*弹出栈T的元素,赋给j,p指向j的后继事件k*/
{
k=p->adjvex;
dut=*(p->info); /*dut为弧的权值*/
if(vl[k]-dutnextarc)
{
k=p->adjvex;
dut=*(p->info); /*dut为弧的权值*/
e=ve[j]; /*e就是活动的最早开始时间*/
l=vl[k]-dut; /*l就是活动的最晚开始时间*/
printf("%s→%s %3d %3d %3d\n",N.vertex[j].data,N.vertex[k].data,e,l,l-e);
if(e==l) /*将关键活动保存在数组中*/
{
e1[count]=j;
e2[count]=k;
count++;
}
}
printf("关键活动为:");
for(k=0;k - 有向网的创建
int LocateVertex(AdjGraph G,VertexType v)
/*返回图中顶点对应的位置*/
{
int i;
for(i=0;ivexnum);
for(i=0;ivexnum;i++) /*将顶点存储在头结点中*/
{
scanf("%s",N->vertex[i].data);
N->vertex[i].firstarc=NULL; /*将相关联的顶点置为空*/
}
printf("请输入弧尾、弧头和权值(以空格作为分隔):\n");
for(k=0;karcnum;k++) /*建立边链表*/
{
scanf("%s%s%*c%d",v1,v2,&w);
i=LocateVertex(*N,v1);
j=LocateVertex(*N,v2);
/*j为弧头i为弧尾创建邻接表*/
p=(ArcNode*)malloc(sizeof(ArcNode));
p->adjvex=j;
p->info=(InfoPtr*)malloc(sizeof(InfoPtr));
*(p->info)=w;
/*将p指向的结点插入到边表中*/
p->nextarc=N->vertex[i].firstarc;
N->vertex[i].firstarc=p;
}
(*N).kind=DN;
} - 有向网的输出
void DisplayGraph(AdjGraph N)
/*网的邻接矩阵N的输出*/
{
int i;
ArcNode *p;
printf("该网中有%d个顶点:",N.vexnum);
for(i=0;i ",N.vertex[i].data,N.vertex[p->adjvex].data,*(p->info));
p=p->nextarc;
}
printf("\n");
}
} - 有向网的销毁
void DestroyGraph(AdjGraph *N)
/*销毁无向图G*/
{
int i;
ArcNode *p,*q;
for(i=0;ivexnum;++i) /*释放网中的边表结点*/
{
p=N->vertex[i].firstarc; /*p指向边表的第一个结点*/
if(p!=NULL) /*如果边表不为空,则释放边表的结点*/
{
q=p->nextarc;
free(p);
p=q;
}
}
(*N).vexnum=0; /*将顶点数置为0*/
(*N).arcnum=0; /*将边的数目置为0*/
} - 主程序
void main()
{
AdjGraph N;
CreateGraph(&N); /*采用邻接表存储结构创建有向网N*/
DisplayGraph(N); /*输出有向网N*/
CriticalPath(N); /*求网N的关键路径*/
DestroyGraph(&N); /*销毁网N*/
}- 测试结果