摄像机标定学习笔记(1)对张正友标定方法的理解
原创文章,欢迎转载,转载请注明出处。
一、摄像机标定成像原理
(1)靶标平面与其图像平面之间的映射关系
在相机针孔成像模型下,假设点p 为靶标平面上的一点,点p在世界坐标系下的坐标为 M=(Xwi,Ywi,Zwi) ,其齐次坐标为 M’(Xwi,Ywi,Zwi,1) ,像点 p′在图像坐标系下的坐标为 m=(ui,vi) ,齐次坐标表示为 m=(ui,vi,1) 。根据直接线性变换,将像点和物点的成像几何关系在齐次坐标下写成透视投影矩阵的形式如公式(1)所示: 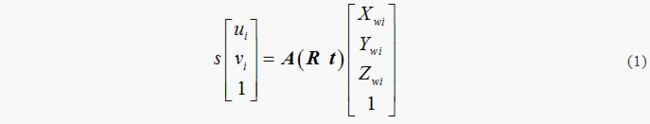
上式中, s为任意非零未知尺度因子。矩阵A为相机的内参数矩阵,R为3×3单位正交旋转矩阵。t为3×1的平移矢量,矩阵A、R的具体形式为:
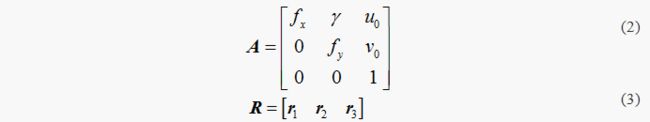
式中:fx和fy分别为u轴和v轴的尺度因子,γ为倾斜因子,且当u轴和v轴垂直时γ=0。u0、v0为光轴中心的图像坐标即主点坐标(或者表示CCD相机的光轴中心在图像平面的坐标)。旋转矩阵R的第i列元素由 ri 表示。将(2)、(3)式代入(1)式,可得:
假设靶标平面位于世界坐标系的OwXwYw平面上,即Zwi=0.由上式可得:
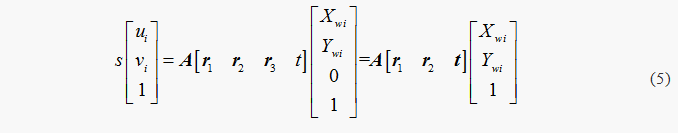
这里,仍采用M来表示靶标平面上的点,则齐次坐标形式为M一横=[Xwi,Ywi,1]T,则靶标平面上的点M与对应图像点m之间的对应关系可表示为一个单应性矩阵 H,即:
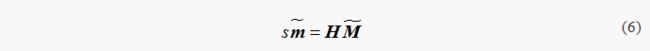
(2)求解摄像机参数矩阵
上式中 H=λA[r1 r2 t]为一个3×3的矩阵,根据公式(6),在拍摄的图像获取至少4个点后,若已知标定特征点的世界坐标(Xwi,Zwi,1)及其像素坐标(ui,vi,1),便可计算出单应性矩阵 H,从而完成标定。令 H=[h1 h2 h3] ,单应性矩阵 H 的第i列元素由 hi表示,其中λ为一常数因子,于是有:
![]()
根据旋转矩阵 R 的单位正交特性(r1T *r2 =0; r1T r1 =r2T r2 ), 可得到如下两个基本内参数约束矩阵。

上式中的 h1,h2 是通过求解单应性矩阵 H 求得, 所以未知量只剩下内参矩阵 A 。若考虑倾斜因子 γ, 则 A 中含有5个未知参数,则完全解出来这5个未知量,则需要3个不同的单应性矩阵 H , 即至少需要已知三组像平面与物平面的映射关系便可完成对相机内参数的标定。其中 A-T = (A-1 ) T = (AT ) -1 ,则令 B = A-TA-1= (A AT) -1,则 B为对称矩阵,将(2)式代入下式可得:
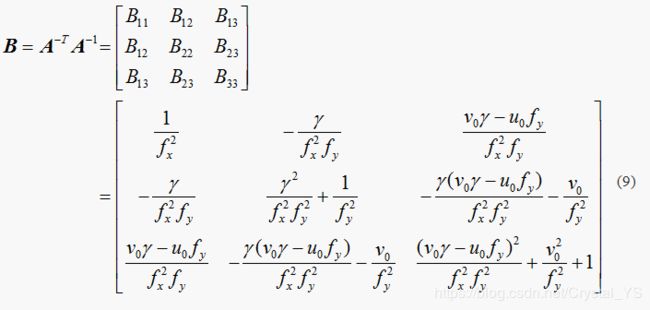
设向量 b =[B11, B12, B22, B13, B23, B33] ,单应性矩阵 H 中的第i列向量为 hi =[h11, h12 ,h13] ,则有:

其中 vij =[hi1hj1,hi1hj2+hi2hj1,hi2hj2,hi3hj1+hi1hj3, hi3hj2+hi2hj3, hi3hj3]T; 于是(7)式可以改写成两个关于 b 为未知数的内部参数约束关系的齐次方程如下:

若有n组光刀平面与相机像平面的映射关系,将n个这样的方程组叠起来,可得:
![]()
其中 V 为2n×6的矩阵,当n≥3 ,b 可以在相差一个尺度因子的意义下唯一确定即至少存在3组光刀平面与相机像平面的映射关系,便可唯一确定矩阵 b。如果n=2,可以加上一个附加约束γ=0,即B12=0。因此可以用 [0 1 0 0 0 0] b=0作为公式(12)的一个附加条件 ,式(11)的解是矩阵 VTV 的最小特征值对应的特征向量,或通过对矩阵 V 进行奇异值分解(SVD),求解出 b。
当 b 求解出后,可构造出矩阵 B,再对 A-T A-1求逆得到 A AT,对 A AT用Cholesky矩阵分解算法求解出相机的内参数矩阵 A,或在相差一个尺度因子 λ1 下,B= λ1A-TA-1 由绝对二次曲线的性质,得到相机的内参数如下:
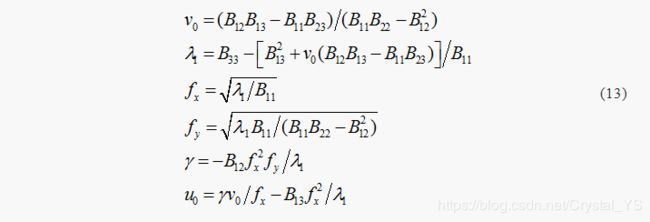
在内参数矩阵 A 求出后,每组映射关系的外参数就容易求出,由式(7)有:

其中,

通常情况下,相机镜头是有畸变的,因此,上述获得的参数作为初值,进行优化搜索,从而计算出所有参数准确值。由上述分析可知,即至少需要已知三组像平面与物平面的映射关系,便可完成对相机内、外参数的标定。
二、标定原理的解释及注意事项
(1).标定原理解释
a.求解单应性矩阵 H 至少需要已知靶标平面上的四个点。
单应性矩阵 H 是一个3×3的矩阵,其最后一个元素值即为1,而其它8个元素值都为未知量,这8个未知量的求取方法为:当靶标平面上已知坐标的点数N≥4时,2N≥8,方程组中方程个数大于未知量个数,即可求解得到单应性矩阵 中的8个未知量,从而完成线结构光系统的标定。

ps:由于单应性矩阵表征了像面与物面之间的映射关系,所以在求解过程中要保证每个点的图像坐标(ui,vi)和世界坐标(Xwi,Ywi)要一一对应。
b.在五个未知参量都未知的情况下,求解内参数矩阵***A***至少需要三幅图片
- 在焦距(fx,fy)、主点(u0,v0)和倾斜因子γ未知大小的情况下,至少需要三幅图片(三种姿态的图片)便可以计算出内参数矩阵 A。
- 在焦距(fx,fy)、主点(u0,v0)未知大小和倾斜因子γ=0的情况下,至少需要两幅图片(两种姿态的图片)便可以计算出内参 A。
- 在焦距(fx,fy)未知、主点(u0,v0)已知倾斜因子γ=0的情况下,至少需要一幅图片(一种姿态的图片)便可以计算出内参数矩阵 A。

ps:因为内参数矩阵 A 一共有五个未知参数,分别是焦距(fx,fy)、主点(u0,v0)和倾斜因子γ,解出五个未知参数至少需要五个方程 ,由公式(8)可知,一幅图提供两个方程,所以在五个未知参量都未知的情况下,至少需要三幅图片(三种姿态的图片)便可以计算出内参数矩阵 A。
(2).注意事项
a. 实验过程说明
在拍摄靶标图像时,先关闭采集图片设备预设置量,再相机光圈调大,此时曝光量较大,然后调节相机的焦距,保证分辨率测试图卡在移动的某个范围内成像清晰。
采集靶标图像时应特别注意,需要在不同的角度不同的位置采集靶标的多幅图像。采集到的图像必须清晰,靶标图像尺寸以占整幅图像尺寸的1/3~3/4为宜。
靶标图像最好在整幅图像的不同位置都有分布,不宜过于集中于同一区域。靶标放置位置与摄像机之间的距离最好为视觉系统的主要工作距离。
靶标相对于摄像机的角度应有较大范围的变化,应包含绕三个轴较大角度的旋转,最好不小于30度。
采集的靶标图像数量不应太少,建议以10~20幅靶标图像为宜。
采集图像过程中,摄像机的焦距不能调整。因为焦距属于摄像机的内参数,不同焦距下采集的图像隐含了不同的内参数,这些图像放在一起进行标定不能得到正确的结果。
b. 对单应性矩阵H的理解
单应性矩阵H(Homography)两部分组成:用于定位观察的物体平面的物理变换和使用摄像机内参矩阵的投影。物理变换部分是与观测到的图像平面相关的部分旋转 R 和部分平移 t 的影响之和,描述了二维图像平面与三维世界坐标系平面之间的位置映射关系,对应的变换矩阵称为单应性矩阵。H=[h11 h12 h13;h21 h22 h23;h31 h32 h33 ]
单应矩阵H的自由度为8个。一个点可以得到两个方程,而H有9个参数8个自由度(h33=1),也就是只需要求解8个参数。因此至少需要4个点,才能解出一个H,一般标定板上的点比较多,其他的点是为了优化H的。在张的方法中,摆放不同姿态的靶标,会得到不同的单应性矩阵H。
单应性在计算机视觉中的应用。
a.用于在相机的内参数的标定
b.视角变换
c.图像拼接:
d.相机位姿估计
e.增强现实(AR)
f.视觉SLAM
g.图像校正
(关于单应性矩阵具体应用的实现过程,请看作者后续博客。)
c. 对内参数和外参数的理解
在标定过程中,摄像机内部参数始终保持不变,即不论摄像机从任何角度拍摄靶标,摄像机的内部参数都为常数,只有外部参数发生变化。标定过程中每一个姿态都有自己的外参数。即靶标摆放以不同的姿态得到的外参数(R=[r1 r2 r3],t)都不同。因为H = λA[r1 r2 t],所以每个面得到的单应性矩阵H 也不一样。
世界坐标系(Xw,Yw,Zw)->相机坐标系(Xc,Yc,Zc):
摄像机的外参数: 旋转向量(大小为1×3的矢量或旋转矩阵3×3)和平移向量t。
R 为3×3矩阵,t为3×1矩阵,表示世界坐标系原点与摄像机坐标系原点的关系,0为(0,0,0),旋转矩阵R是坐标轴依次绕x,y和z轴旋转角度ψ,φ和θ,所形成的三个矩阵 Rx(ψ),Ry(φ),Rz(θ)的总乘积。

旋转矩阵 R 的计算公式为:
