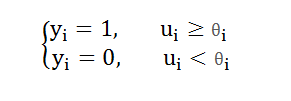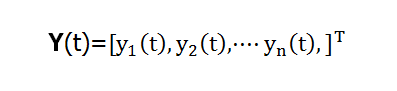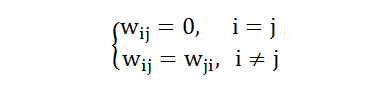MATLAB神经网络编程(九)——Hopfield网络
《MATLAB神经网络编程》 化学工业出版社 读书笔记
第六章反馈型神经网络 6.1 Hopfield网络
本文是《MATLAB神经网络编程》书籍的阅读笔记,其中涉及的源码、公式、原理都来自此书,若有不理解之处请参阅原书
前馈神经网络与反馈神经网络
根据神经网络运行过程中的信息流向,可将神经网络分为前馈式和反馈式两种基本类型。前馈网络即通过引入隐层以及非线性转移函数,网络具有复杂的非线性映射能力。但前馈网络的输出仅仅由当前输入和权值矩阵决定,而与网络先前的输出状态无关。
在前馈网络中,不论是离散型还是连续型,一般均不考虑输出与输入之间在时间上的滞后性,而只表达两者之间的映射关系。但在Hopfield网络中,考虑了输出与输入之间延迟因素,因此,需要用微分方程或者差分方程来描述网络的动态数学模型。
神经网络的学习方式有3种类型其中,有导师学习方式(有监督学习)和无导师学习(无监督学习)方式在前面章节均有涉及。第三类学习方式是“灌输式”,即网络的权值不是经过反复学习获得的,而是按照一定规则事先计算出来的。Hopfield神经网络就是采用了这种学习方式,其权值一经确定就不在改变,而网络中各个神经元的状态在运行过程中不断更新,网络由演变到稳定时各神经元的状态是问题之解。
本章主要介绍的就是反馈型神经网络,也称为递归网络或者回归网络。与前面学习过的感知器、线性神经网络、或径向神经外等前向型神经网络不同在于,反馈神经网络的输入包含有延迟的输入或者输出数据的反馈。由于是有反馈的输入,所以它是一种反馈动力学习系统。这种系统的学习过程就是他的神经元状态的变化过程,这个过程最终会达到一个神经元状态不变的稳定态,同时标志着学习过程结束。反馈神经网络的这种动态学习特性,主要由网络的反馈形式决定。反馈网络的反馈形式是比较多样化的,有输入延迟的、单层输出反馈的、神经网络自反馈的、两层之间互相反馈等。
6.1 Hopfield网络
Hopfield神经网络模型是一种循环神经网络,从输出奥输入由反馈连接。Hopfield网络分为两种:
- 离散型Hopfield网络
- 连续型Hopfield网络
由于反馈神经网络的输出端又反馈到其输入端,所以,Hopfield网络在输入的激励下,会产生不断的状态变化。当在输入之后,可以求出Hopfield的输出,这个输出反馈到输入端从而产生新的输出,这个反馈过程一直反复进行。如果Hopfield网络是一个具有收敛的稳定网络,则这个反馈与迭代的计算过程所产生的变化越来越小,一旦到达了稳定的平衡状态,Hopfield网络就会输出一个稳定的恒值。对于一个Hopfield网络来说,关键在于确定它在稳定条件下的权系数。
注意,反馈网络有稳定的,也有不稳定的。对于Hopfield网络来说,还存在如何判断它是稳定的、或者不稳定的问题。而判断的依据是什么,也是需要确定的。
6.1.1 离散Hopfield网络
Hopfield最早提出的网络是二值神经网络,神经元的输出只取1和0,所以也称为离散Hopfield神经网络(Discrete Hopfield Neural Network,DHNN)。在DHNN中,所采用的神经元是二值神经元;因此,所输出的离散值1和0分别表示神经元处于激活和抑制状态。
1,网络结构
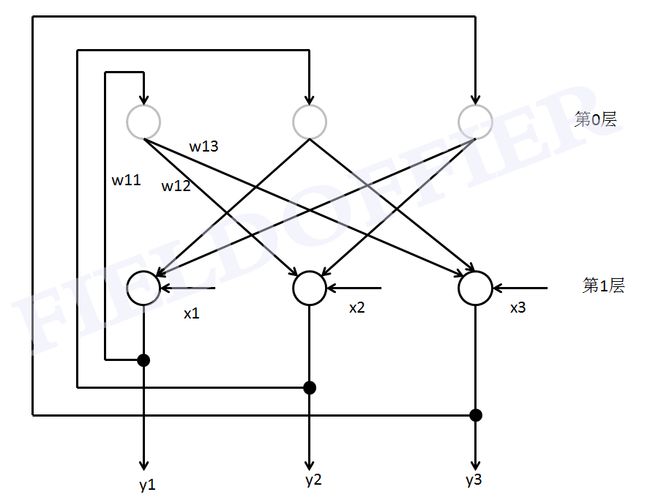
DHNN是一种单层的、其输入/输出为二值的反馈网络。假设一个由三个神经元组成的离散Hopfield神经网络,其结构如下:
上图中,第0层仅仅是作为网络的输入,它不是实际神经元,所以无计算功能;第一层是神经元,故而执行对输入信息和权系数乘积求累加和,并经非线性函数f处理之后产生输出信息。f是一个简单的阈值函数,如果神经元的输出信息大于阈值θ,那么,神经元的输出取值为1,;小于阈值θ,则神经元的输出取值为0。
对于二值神经元它的计算公式:

上式中,xj是外部输入。
注意上面公式中没有偏移矩阵b,xj充当了偏移矩阵的功能,虽然它是外部输入。这是与感知器、线性神经网络极大的区别
并且有:
一个DHNN的网络状态是输出神经元信息的集合。对于一个输出层是n个神经元的网络,其t时刻的状态为一个n维向量:
因为yi(t)(i=1,2,···,n)可以取值为1或0,故n维向量Y(t)有2^n种状态,即网络有2^n种状态。
对于有三个神经元的DHNN,它的输出层就是三位二进制数;每一个三位二进制数就是一种网络状态,共有2^3=8个网络状态,这些网络状态如图所示:
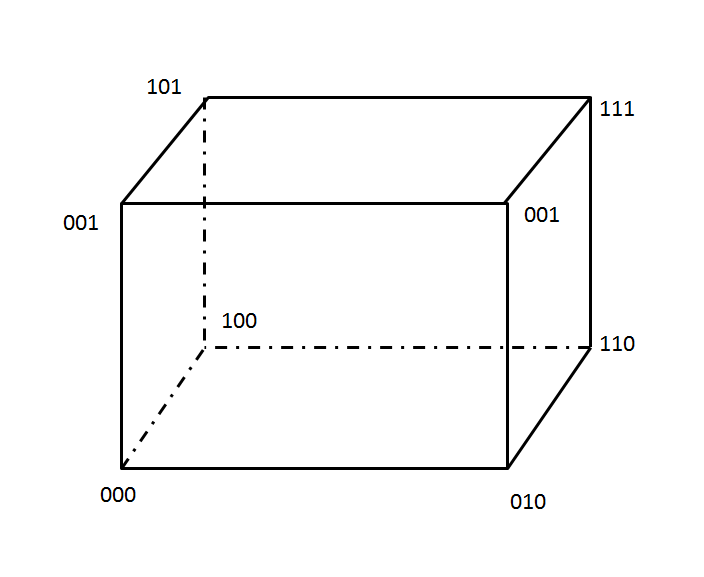
在上图中,立方体的每一个顶点表示一种网络状态。同理,对于n个神经元的输出层,有2^n中网络状态,也和一个n维超立方体的顶角相对应。
如果Hopfield网络是一个稳定网络,如在网络的输入端加入一个输入向量,则网络的状态会产生变化,即从超立方体的一个顶角转向另一个顶角,并且最终稳定于一个特定的顶角。
对于一个n个神经元组成的DHNN,有n*n权系数矩阵W:
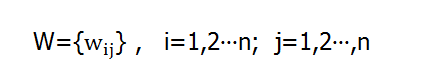
同时,有n维阈值向量θ:
一般而言,W和θ可以确定一个唯一的DHNN。对于上面所说的三个神经元组成的Hopfield网络,也可以改用下图的图形表示,这两个图形的意义是一样的:
2,网络的工作方式
DHNN有两种不同的工作方式。
(1)串行(异步)方式
在时刻t时,只有某一个神经元j的状态发生变化,而其他n-1个神经元的状态不变,这里称为串行工作方式。并且有:

(2)并行(同步)方式
在任一时刻t,所有的神经元的状态都产生了变化,则称为并行工作方式。并且有:

3,网络的稳定性
对于一个反馈网络来说稳定性是一个重大的性能指标。
假设一个DHNN,其状态为Y(t):
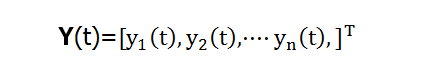
如果对于任何Δt>0,当神经网络从t=0开始,有初始状态Y(0)。经过有限时刻t,有:
Y(t+Δt)=Y(t)
则认为网络是稳定的。串行方式下的稳定性称为串行稳定性;并行方式下的稳定性称为并行稳定性神经网络稳定时,其状态称为稳定状态。
从DHNN可以看出,它是一种多输入、含有阈值的二值非线性动态系统。在动态系统中,平衡稳定状态可以理解为系统某种形式的能量函数在系统运行过程中,其能量不断减少,最后处于最小值。
关于稳定性的含义以及Hopfield网络的能量函数问题,实在是太复杂了,而且我也看不懂,所以就不写了,有兴趣的可以去看看书。——by SnowNight
Hopfield网络稳定的充分条件:如果Hopfield网络的权系数矩阵W是一个对称矩阵,并且对角线元素为0,则这个网络是稳定的。即在权系数矩阵W中,如果:
注意:上述是充分条件,仅仅是充分条件,实际上很多稳定的Hopfield网络的权值系数矩阵W都不是对称的。——by BADaPPLE
因此,无自反馈的权系数对称Hopfield网络是稳定的网络,其结构图如下:
4,联想记忆功能
Hopfield网络的一个重要功能是可以用于联想记忆,即联想存储器,这是人类的智能特点之一。
关于联想记忆功能后面会有单独文章分析——by NIGHTwISH
6.1.2 连续Hopfield网络
1,网络结构
连续Hopfield神经网络(Continuous Hopfield Neural Network,CHNN)的拓扑结构与DHNN的结构相同。这种拓扑结构和生物神经系统中大量存在的神经反馈回路 是一致的。
2,网络稳定性
和DHNN一样,CHNN稳定条件也要求:

CHNN与DHNN不同之处在于其函数g不是阶跃函数,而是S型的连续函数。一般取:

CHNN在时间上是连续的,所以,网络中各个神经元是处于同步方式工作的。对于一个神经细胞,即神经元j,其内部膜电位状态用Uj表示,细胞膜输入电容是Cj,细胞膜的传递电阻是Rj,输出电压是Vj,外部输入电流用Ij表示,则CHNN可用下图电流图表示:

这是啥?初中物理?好像很眼熟的样子,上大学前我一定是看得懂的吧,现在反正只能做个样子了——by WHITEwISHES
对于连续Hopfield网络,Hopfield给出如下稳定性定理:
不好意思,公式太复杂了,我懒得贴上来了——by SOMEbODY
还是直接给出结论吧:当Hopfield网络的神经元传递函数g是连续且有界的(如Sigmoid函数),并且网络的权值系数矩阵对称,则这个连续Hopfield网络是稳定的。
在实际应用中,任何一个系统,如果其优化问题可以用能量函数E(t)作为目标函数,那么总可以用连续Hopfield网络对其进行求解。由于引入能量函数E(t),Hopfield神经网络和优化问题直接对应,这种工作是具有开拓性的。利用神经网络进行优化计算,就是在神经网络和一动态系统中给出初始的估计点,即初始条件,然后随网络在运动传递中找到相应的极小点。这样,大量优化问题都可以用连续的Hopfield网络来求解。这也是Hopfield网络用于神经计算的基本原因。