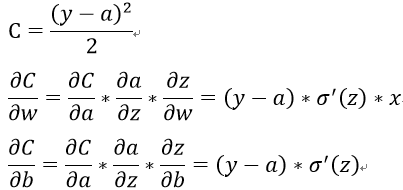交叉熵、L2规范化、权重初始化推导，改进Michael Nielsen神经网络（2）

问题一：

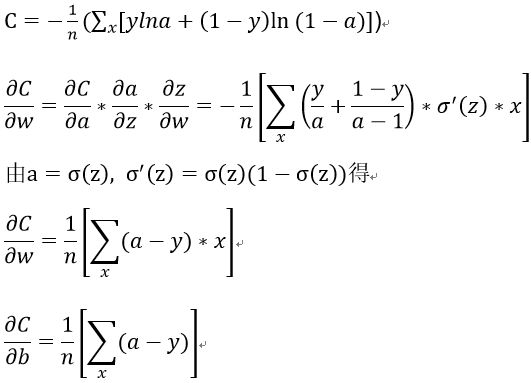
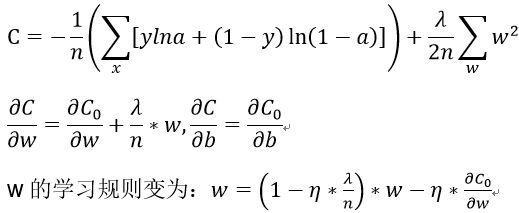
       使用二次代价函数时，当神经网络在犯错较大的情况时（w，b值偏离较大，如初始值给的太大），学习缓慢，即

较小。

       当遇到错误数据时，神经元输出易饱和，使得激活函数导数接近0，学习速度缓慢。所以想要使得偏导数里不出现 sigmoid激活函数的导数，引入交叉熵代价函数。

一、交叉熵代价函数

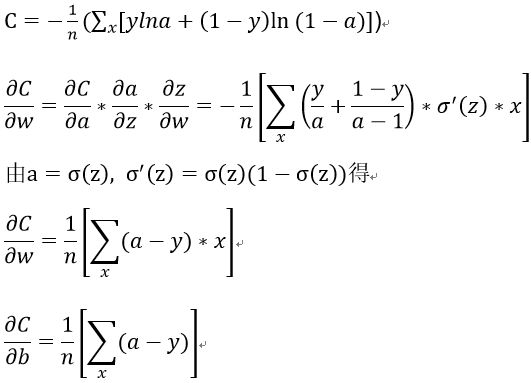
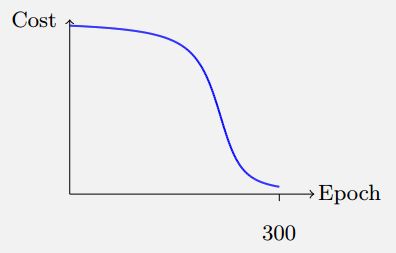
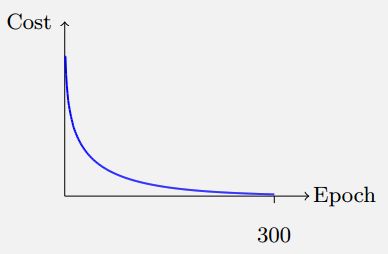
       使用交叉熵后，神经网络犯错误时学习速度更快。前后比较示意图：

                     

问题二：

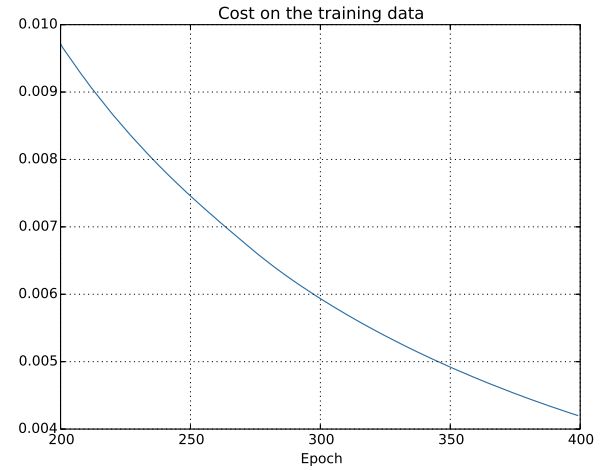
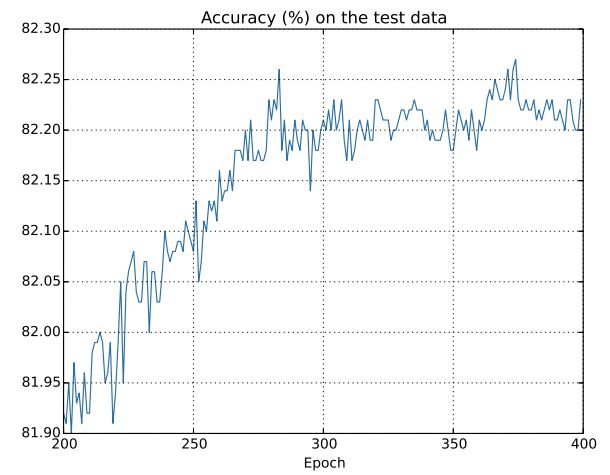
       当神经网络在测试集上准确率已接近不变，而网络学习时代价函数还在持续下降，同时测试集的代价函数先下降后上升，产生了过拟合现象。解决过拟合的其中一种方法就是规范化。示意图：

                   

二、规范化

规范化交叉熵：

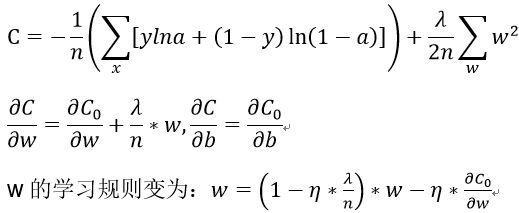
       在较小的代价函数和较小的权重中取一个折中。如果代价函数是⽆规范化的，那么权重向量容易朝着一个方向变化受困于一个局部最优解。更⼩的权重意味着⽹络的⾏为不会因为我们随便改变了⼀个输⼊⽽改变太⼤。这会让规范化⽹络学习局部噪声的影响更加困难。

 

问题三：

    若权重w，b初始化符合归一化的高斯分布，则假设有1000个输入，500个为1,500个为0，则 ，z的标准差为 ，z是一个很宽的高斯分布，可能导致|z|>>1，使隐藏的神经元饱和，导致学习缓慢。

    可以使用均值为0，标准差为 的高斯分布初始化权重，使高斯函数更加尖锐，神经元不容易饱和，不改变网络性能，但提升了学习速度。

改进后代码：

# -- coding: utf-8 --
import random
import numpy as np
import mnist_loader

# 定义二次损失函数和交叉熵损失函数
'''
class QuadraticCost(object):

    @staticmethod
    def fn(a, y):
        return 0.5*np.linalg.norm(a-y)**2

    @staticmethod
    def delta(z, a, y):
        # 输出层dz
        return (a-y) * sigmoid_prime(z)
'''

class CrossEntropyCost(object):

    @staticmethod
    def fn(a, y):
        # np.nan_to_num使nan变成0，无穷变成衣蛾很大的数
        return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))

    @staticmethod
    def delta(z, a, y):
        return (a-y)


# network类
class Network(object):

    def __init__(self, sizes, cost=CrossEntropyCost):
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.default_weight_initializer()
        self.cost = cost

    def default_weight_initializer(self):
        # 归一化高斯分布初始化
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        # 标准差为根号n的高斯分布初始化
        self.weights = [np.random.randn(y, x)/np.sqrt(x)
                        for x, y in zip(self.sizes[:-1], self.sizes[1:])]

    def feedforward(self, a):
        # 前向传播
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            # 随机梯度下降
            lmbda = 0.0,
            evaluation_data=None,
            monitor_evaluation_cost=False,
            monitor_evaluation_accuracy=False,
            monitor_training_cost=False,
            monitor_training_accuracy=False):
        if evaluation_data: n_data = len(evaluation_data)
        n = len(training_data)
        evaluation_cost, evaluation_accuracy = [], []
        training_cost, training_accuracy = [], []
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(
                    mini_batch, eta, lmbda, len(training_data))
            print "Epoch %s training complete" % j
            if monitor_training_cost:
                cost = self.total_cost(training_data, lmbda)
                training_cost.append(cost)
                print "Cost on training data: {}".format(cost)
            if monitor_training_accuracy:
                accuracy = self.accuracy(training_data, convert=True)
                training_accuracy.append(accuracy)
                print "Accuracy on training data: {} / {}".format(
                    accuracy, n)
            if monitor_evaluation_cost:
                cost = self.total_cost(evaluation_data, lmbda, convert=True)
                evaluation_cost.append(cost)
                print "Cost on evaluation data: {}".format(cost)
            if monitor_evaluation_accuracy:
                accuracy = self.accuracy(evaluation_data)
                evaluation_accuracy.append(accuracy)
                print "Accuracy on evaluation data: {} / {}".format(
                    self.accuracy(evaluation_data), n_data)
            print
        return evaluation_cost, evaluation_accuracy, training_cost, training_accuracy

    def update_mini_batch(self, mini_batch, eta, lmbda, n):
        # 更新w，b
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]

    def backprop(self, x, y):
        # 反向传播
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # 前向传播
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # 反向传播
        delta = (self.cost).delta(zs[-1], activations[-1], y)
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())

        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

    def accuracy(self, data, convert=False):
        # 返回准确数据数
        if convert:
            results = [(np.argmax(self.feedforward(x)), np.argmax(y))
                       for (x, y) in data]
        else:
            results = [(np.argmax(self.feedforward(x)), y)
                        for (x, y) in data]
        return sum(int(x == y) for (x, y) in results)

    def total_cost(self, data, lmbda, convert=False):
        # 返回数据集的总损失，如果数据集是训练集则convert=False，验证集或测试集=True
        cost = 0.0
        for x, y in data:
            a = self.feedforward(x)
            if convert: y = vectorized_result(y)
            cost += self.cost.fn(a, y)/len(data)
        cost += 0.5*(lmbda/len(data))*sum(
            np.linalg.norm(w)**2 for w in self.weights)
        return cost


def vectorized_result(j):
    # 返回一个十行一列的数组
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e


def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))


def sigmoid_prime(z):
    return sigmoid(z)*(1-sigmoid(z))

training_data, validation_data, test_data = mnist_loader.load_data_wrapper()
net = Network([784, 30, 10], cost=CrossEntropyCost)
net.SGD(training_data, 30, 10, 0.1, lmbda = 5.0,evaluation_data=validation_data,monitor_evaluation_accuracy=True)

output：