带权并查集（含种类并查集）【经典模板】 例题：①POJ 1182 食物链（经典）②HDU - 1829 A bug's life（简单） ③hihoCoder 1515 : 分数调查

带权并查集

---

• 带权并查集，即增加了一个value，然后在合并过程中就需要维护这个值。
• 种类并查集，就是元素分为不同种类，实际上可以转化为带权并查集来处理。当然也有种类并查集的自己的解法。

下面以【 POJ 1182 食物链（经典）】 【HDU - 1829 A bug’s life（简单）】两个题为例，分别用带权并查集和种类并查集的解法给出。
【hihoCoder 1515 : 分数调查】给出带权并查集的解法。

---

---

例题一 ：POJ 1182 食物链（经典）

POJ 1182 食物链

Description
动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是"1 X Y"，表示X和Y是同类。
第二种说法是"2 X Y"，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1） 当前的话与前面的某些真的话冲突，就是假话；
2） 当前的话中X或Y比N大，就是假话；
3） 当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。

Input
第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。

Output
只有一个整数，表示假话的数目。

Sample Input

100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5

Sample Output

3

***比较好的两个讲解博客：***(以下主要搬自这两个博客）
Algorithm带权并查集
【POJ1182】食物链，思路+数据+代码，可能是史上关于这道题最详细的解题报告
部分测试数据
测试数据

题意：
动物王国中有三类动物A，B，C，构成环形：A吃B，B吃C，C吃A。

现有N个动物，从1开始编号，每个动物都是A，B，C中的一种，但我们并不知道是哪一种。

用两种说法描述这N个动物的食物链关系：

1 X Y 表示X和Y是同类
2 X Y 表示X吃Y

给出K句话，有些是真的，有些是假的，满足下列任一条件即为假话，否则是真话：

当前的话与之前的某些真话冲突
当前的话中X或Y比N大
当前的话表示X吃X

输出假话的总数。

1、带权并查集解法
定义两个数组fa[ ]和rela[ ]，fa用来判断集合关系，rela用来描述其与根节点的关系。因为关系满足传递性，所以可以推导出给出条件下的当前关系，在判断与之前已有关系是否矛盾。

本题的解法巧妙地利用了模运算，rela数组用0表示同类，1表示当前点能吃别人，2表示当前点被别人吃。

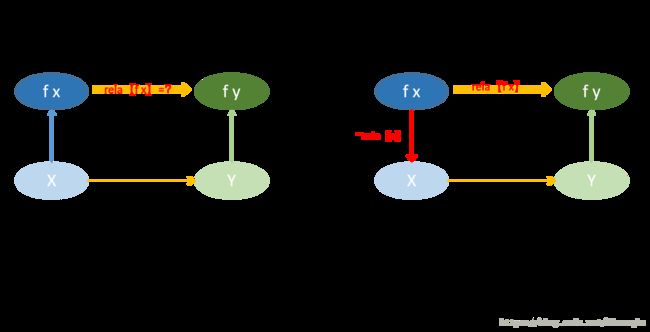
- 路径压缩时： relation[x] = relation[x]*relation[fa[x]] - 合并时： relation[fx] = (-relation[x])*relationxy*relation[y] 其中“*”是关系运算，“-”是取**对称**关系

---

传递性推导【按照图示推导】

---

传递性推导【按照表格推导】

1、已知两点AB和根的关系，推导任意两点AB之间的关系

结点A与根关系	结点B与根关系	A与B关系
0	0	0
0	1	2
0	2	1
1	0	1
1	1	0
1	2	2
2	0	2
2	1	1
2	2	0

那么知道了两点AB和根的关系，就可以知道任意两点AB之间的关系=为

relation（A->B） = ( rela[a] - rela[b]) % 3

那么我们就可以根据这个关系，判断输入的话语中AB的关系是否正确了。

注意啦！这里出现了相减，因此要注意产生负数的情况，要加上一个3，防止出现负数，同时3%3也不会对结果有影响。

bool check(int r, int x, int y)
{
   if(x > n || y > n)
        return false;
   if(r == 1 && x == y)
    return false;
   if(find(x) == find(y))
   {
       //根据前面正确描述得出的正确的关系
       int relation = ((rela[x] - rela[y]) + 3) % 3;//+3防止出现负号
       return relation == r;
   }
   else
    return true;
}

2、已知某一点A与根的关系，及AB的关系，推导B与根之间的关系

结点A与根关系	A与B关系	结点B与根关系
0	0	0
0	1	1
0	2	2
1	0	1
1	1	2
1	2	0
2	0	2
2	1	0
2	2	1

那么知道了某一点A与根的关系，及AB的关系，我们就可以推导出B与根之间的关系。那么在find过程中，我们就可以利用路径压缩维护这种关系，通过当前点B到父节点A的关系，加上父节点A与根的关系，维护当前点B与根的关系。

rela[b] = (rela[b] + rela[a]) % 3

int find(int x)
{
    if(fa[x] == x)
        return x;
    else
    {
        int temp = fa[x];
        fa[x] = find(fa[x]);
        rela[x] = (rela[x] + rela[temp]) % 3;
        return fa[x];
    }
}

3、已知A与根RA的关系，B与根RB的关系，以及AB之间的关系，推导RA和RB的关系

结点A与根RA关系	结点B与根RB关系	B与A关系	根RB与根RA的关系
0	0	0	0
0	0	1	1
0	0	2	2
0	1	0	2
0	1	1	0
0	1	2	1
0	2	0	1
0	2	1	2
0	2	2	0

知道A与根RA的关系，B与根RB的关系，以及AB之间的关系，就可以知道RA和RB的关系了。那么在merge过程中，我们就可以在合并两根时，推导出两根关系。

rela[rb] = rela[a] - rela[b] + rela[b -> a]

这里要注意若是要求RB和RA的关系（即将RB合并到RA上面），是用A - B + (B 与A的关系！而非A与B的关系）

注意啦！这里出现了相减，因此要注意产生负数的情况，要加上一个3，防止出现负数，同时3%3也不会对结果有影响。

void merge(int r, int x, int y)
{
    int fx = find(x), fy = find(y);
    if(fx != fy)
    {
        fa[fx] = fy;
        rela[fx] = (rela[y] - rela[x] + r + 3) % 3;//+3是为了防止这里相减产生负数
    }
}

PS： 在本题中需要注意的是传入的relation恰为描述的种类号减一。也就是说要提前将输入的描述号做-1处理后传入函数中。

综上所述：

AC代码

#include 
#include 
using namespace std;

const int MAXN = 50005;

int fa[MAXN], rela[MAXN];
int n, k, ans;

void init()
{
    for(int i = 1; i <= n; i++)
    {
        fa[i] = i;
        rela[i] = 0;
    }
    ans = 0;
}

int find(int x)
{
    if(x == fa[x])
      return x;
    else
    {
        int temp = fa[x];
        fa[x] = find(fa[x]);
        rela[x] = (rela[x] + rela[temp]) % 3;
        return fa[x];
    }
}

//以下的r均为处理过的relation，0表示同类，1表示x吃y，2表示x被y吃
//也就是说这里的r为题目所给编号-1
void merge(int r, int x, int y)
{
    int fx = find(x), fy = find(y);
    if(fx != fy)
    {
        fa[fx] = fy;
        rela[fx] = (rela[y] - rela[x] + r + 3) % 3;//+3是为了防止这里相减产生负数
    }
}

bool check(int r, int x, int y)
{
   if(x > n || y > n)
        return false;
   if(r == 1 && x == y)
    return false;
   if(find(x) == find(y))
   {
       int relation = ((rela[x] - rela[y]) % 3 + 3) % 3;//根据前面正确描述得出的正确的关系
       return relation == r;
   }
   else
    return true;
}

int main()
{
    scanf("%d%d", &n, &k);
    init();
    while(k--)
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        a--;
        if(check(a, b, c))
            merge(a, b, c);
        else
            ans++;
    }
    printf("%d\n", ans);
    return 0;
}

2、种类并查集解法
（来源《程序设计竞赛》）
对于每只动物i创建3个元素，i-A， i-B, i-C，并用这3xN 个元素建立并查集。
这个并查集的维护信息如下：

• i-X表示“i属于种类X”
• 并查集里的每一个组表示组内所有元素代表的情况都同时发生或不发生（理解关键点）

例如，如果i-A 和i-B在同一个组里，就表示如果i属于种类A那么j一定属于种类B，如果j属于种类B那么i一定属于种类A。因此，对于每一条信息，只需要按照下面进行操作就可以了。

• 第一种，x与y属于同一种类 ———— 合并x-A和y-A, x-B和y-B, x-C和y-C。
• 第二种，x吃y ———— 合并 x-A 和 y-B， x-B 和 y-C， x-C 和 y-A。

注意：合并之前，需要先判断合并是否会产生矛盾。例如 第一种信息下，要检查比如x-A，y-B，y-C是否在同一组等信息。

部分代码：

int N, K;
int T[MAXN], X[MAXN], y[MAXN];//分别表示指令代码，动物A， 动物B

bool same(int x, int y)
{
    return find(x) == find(y);
}

void solve()
{
    //初始化并查集
    //元素X， X+N，X+2*N分别代表x-A， x-B，x-C
    init(N * 3);
    int ans = 0;
    for(int i = 0; i < K; i++)
    {
        int t = T[i];
        int x = X[i] - 1, y = Y[i] - 1;//把输入变为0 ~ N - 1的范围
        //不正确的编号
        if(x < 0 || x >= N || y < 0 || y >= N)
        {
            ans++;
            continue;
        }
        if(t == 1)
        {
            //“x与y属于同一类”的信息
            if(same(x, y + N) || same(x, y + 2 * N))//矛盾
                ans++;
            else
            {
                merge(x, y);
                merge(x + N, y + N);
                merge(x + N * 2, y + N * 2);
            }
        }
        else
        {
            //"x吃y"的信息
            if(same(x, y) || same(x, y + 2 * N))//矛盾
               ans++;
            else
            {
                merge(x, y + N);
                merge(x + N, y + 2 * N);
                merge(x + 2 * N, y);
            }
        }
    }
    printf("%d\n", ans);
}

---

---

例题二 HDU - 1829 A bug’s life（简单）

HDU - 1829 A bug’s life

Background
Professor Hopper is researching the sexual behavior of a rare species of bugs. He assumes that they feature two different genders and that they only interact with bugs of the opposite gender. In his experiment, individual bugs and their interactions were easy to identify, because numbers were printed on their backs.

Problem
Given a list of bug interactions, decide whether the experiment supports his assumption of two genders with no homosexual bugs or if it contains some bug interactions that falsify it.

Input
The first line of the input contains the number of scenarios. Each scenario starts with one line giving the number of bugs (at least one, and up to 2000) and the number of interactions (up to 1000000) separated by a single space. In the following lines, each interaction is given in the form of two distinct bug numbers separated by a single space. Bugs are numbered consecutively starting from one.

Output
The output for every scenario is a line containing “Scenario #i:”, where i is the number of the scenario starting at 1, followed by one line saying either “No suspicious bugs found!” if the experiment is consistent with his assumption about the bugs’ sexual behavior, or “Suspicious bugs found!” if Professor Hopper’s assumption is definitely wrong.

Sample Input
2
3 3
1 2
2 3
1 3
4 2
1 2
3 4

Sample Output
Scenario #1:
Suspicious bugs found!

Scenario #2:
No suspicious bugs found!

Hint
Huge input,scanf is recommended.

题意：
给定多组虫子的交互行为，判断是否有同性恋的情况出现。
PS：注意本题输出要求：每一个样例输出后加一行空行！

1、带权并查集解法
很明显和上面的思路相同，只不过由3种关系变成了2种关系
那么只需要将mod改为2 即可。
（详细解释可以参见博客）

#include 
#include 

using namespace std;

const int MAXN = 2005;
int fa[MAXN], rela[MAXN], n, m, flag;

void init()
{
    for(int i = 0; i <= n; i++)
    {
        fa[i] = i;
        rela[i] = 0;
    }
    flag = 0;
}

int find(int x)
{
    if(fa[x] == x)
        return x;
    else
    {
        int temp = fa[x];
        fa[x] = find(fa[x]);
        rela[x] = (rela[x] + rela[temp]) % 2;
        return fa[x];
    }
}

void merge(int r, int x, int y)
{
    int fx = find(x), fy = find(y);
    if(fx != fy)
    {
        fa[fx] = fy;
        rela[fx] = (rela[y] - rela[x] + r + 2) % 2;
    }
}

bool check(int r, int x, int y)
{
    int fx = find(x), fy = find(y);
    if(fx == fy)
    {
        int relation = (rela[x] - rela[y] + 2) % 2;
        return relation == r;
    }
    else
        return true;
}

int main()
{
    int t;
    scanf("%d", &t);
    for(int i = 1; i <= t; i++)
    {
        scanf("%d%d", &n, &m);
        init();
        while(m--)
        {
            int a, b;
            scanf("%d%d", &a, &b);
            if(check(1, a, b))
                merge(1, a, b);
            else
                flag = 1;
        }
        printf("Scenario #%d:\n", i);
        if(flag == 1)
            printf("Suspicious bugs found!\n\n");
        else
            printf("No suspicious bugs found!\n\n");
    }
    return 0;
}

2、种类并查集解法
（摘自博客）

    #include  
    #include  
    #include  
    #include  
    #include  
    #include  
    #include  
    #include  
    #include  
    #include  
    #include  
    using namespace std;  
    const int MAXN = 10005; /*结点数目上限*/  
    int pa[2*MAXN];    /*2种动物*/  
      
    /*创建一个单元集*/  
    void make_set(int x)  
    {  
        pa[x] = x;  
    }  
      
    /*带路径压缩的查找*/  
    int find_set(int x)  
    {  
        if(x != pa[x])  
            pa[x] = find_set(pa[x]);  
        return pa[x];  
    }  
      
    /*按秩合并x，y所在的集合*/  
    void union_set(int x, int y)  
    {  
        x = find_set(x);  
        y = find_set(y);  
        if(x == y) return;  
        pa[x]=y;  
    }  
      
    int main()  
    {  
      //  freopen("input.txt","r",stdin);  
        int t,n,k,x,y,m=1;  
        scanf("%d",&t);  
        while(t--){  
            /*i~n是男，i+n~i+2*n是女*/  
            for(int i=0;i<2*MAXN;i++)  
                make_set(i);  
            scanf("%d%d",&n,&k);  
            int flag=1;  
            while(k--){  
                scanf("%d%d",&x,&y);  
                if(!flag) continue;  
                if(find_set(x)==find_set(y)||find_set(x+n)==find_set(y+n)){/*是否是同性*/  
                    flag=0;  
                    continue;  
                }else{  
                    union_set(x,y+n);/*男-女*/  
                    union_set(x+n,y);/*女-男*/  
                }  
            }  
            printf("Scenario #%d:\n",m++);  
            if(flag) printf("No suspicious bugs found!\n\n");  
            else printf("Suspicious bugs found!\n\n");  
        }  
    }  

---

---

例题三：hihoCoder 1515 : 分数调查

hihoCoder 1515 : 分数调查

描述

小Hi的学校总共有N名学生，编号1-N。学校刚刚进行了一场全校的古诗文水平测验。
学校没有公布测验的成绩，所以小Hi只能得到一些小道消息，例如X号同学的分数比Y号同学的分数高S分。
小Hi想知道利用这些消息，能不能判断出某两位同学之间的分数高低？

输入

第一行包含三个整数N, M和Q。N表示学生总数，M表示小Hi知道消息的总数，Q表示小Hi想询问的数量。
以下M行每行三个整数，X, Y和S。表示X号同学的分数比Y号同学的分数高S分。
以下Q行每行两个整数，X和Y。表示小Hi想知道X号同学的分数比Y号同学的分数高几分。
对于50%的数据，1 <= N, M, Q <= 1000
对于100%的数据，1 <= N, M, Q<= 100000 1 <= X, Y <= N -1000 <= S <= 1000
数据保证没有矛盾。

输出

对于每个询问，如果不能判断出X比Y高几分输出-1。否则输出X比Y高的分数。
样例输入

10 5 3  
1 2 10  
2 3 10  
4 5 -10  
5 6 -10  
2 5 10  
1 10  
1 5  
3 5

样例输出

-1  
20  
0

思路：
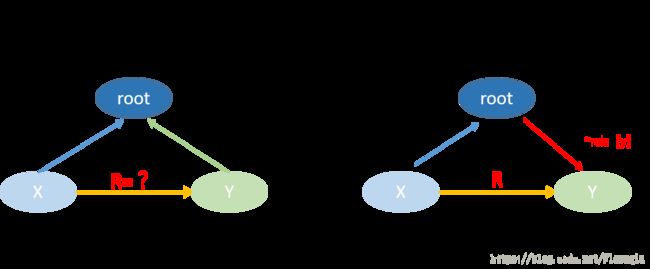
同样使用带权并查集，用数组val记录同学们的权值（与根的分数差，比根高出多少分），那么
路径压缩时（find）：val[x] = val[x] + val[temp];（temp为x的父节点）
合并时（merge）： val[fx] = val[y] - val[x] + s （这里S是x->y的关系，符合公式）
那么要求x比y高多少分，直接输出 val[x] - val[y]即可。

AC代码：

#include 
#include 
using namespace std;

const int MAXN = 100005;
int n, m, q, fa[MAXN], val[MAXN];

void init()
{
    for(int i = 0; i <= n; i++)
    {
        fa[i] = i;
        val[i] = 0;
    }
}

int find(int x)
{
    if(fa[x] == x)
        return x;
    else
    {
        int temp = fa[x];
        fa[x] = find(fa[x]);
        val[x] = val[x] + val[temp];
        return fa[x];
    }
}

void merge(int x, int y, int s)
{
    int fx = find(x), fy = find(y);
    if(fx != fy)
    {
        fa[fx] = fy;
        val[fx] = val[y] - val[x] + s;
    }
}

bool same(int x, int y)
{
    return find(x) == find(y);
}

int main()
{
    scanf("%d%d%d", &n, &m, &q);
    init();
    for(int i = 1; i <= m; i++)
    {
        int x, y, s;
        scanf("%d%d%d", &x, &y, &s);
        merge(x, y, s);
    }
    for(int i = 1; i <= q; i++)
    {
        int x, y, fx, fy;
        scanf("%d%d", &x, &y);
        if(same(x, y))
            printf("%d\n", val[x] - val[y]);
        else
            printf("-1\n");
    }
    return 0;
}