杨振宁论数理关系

摘要: 本文基于杨振宁的相关著述和作者对他的访谈，评述其阐释数理关系时常用的双叶图的寓意，对比说明他多次解释双叶图时所表述含义的微妙差异。杨振宁认为，对待各自的研究成果数学家和物理学家的心理感受完全不同。面对数学的神奇作用，杨振宁与爱因斯坦都产生了十分类似的思想意识，本文详细比较并解读了两位物理巨人的相关思想。离开数学理论物理学家会束手无策，那么理论物理学家可否首先在数学上充分武装自己，然后再展开物理学的研究生涯呢？杨振宁对此的回答是否定的。

关键词: 数学与物理学  纤维丛理论  规范场理论

作为一位理论物理大师，杨振宁能够在自己的研究工作中敏锐发现物理学前沿问题蕴含的数学结构；他在研究物理问题时创立的数学方法与取得的数学成果，促进了20世纪数学的发展。杨振宁指出，“杨-巴克斯方程虽然在物理学中有所应用，但是它对于数学的影响更加巨大。它现在发展得很厉害，在数学领域可谓五花八门，里头的东西有点像数学里的李群。但对它的了解还没像对李群的认识那样清晰，李群的总体结构已经很清楚，在数学里占极为核心的重要地位。”  杨振宁对数学和物理学以及二者之间的关系，有很多独到的思索和感悟，并在其著述及学术报告中，多次阐述自己的观点和态度。这一定意义上说明他对数理关系之奥妙的好奇，以及对这一问题的特殊重视。

一、借助双叶图阐释数理关系

20 世纪物理学的发展使物理学家逐渐认识到，离开数学的支撑，物理学将举步维艰、寸步难行。另一方面，理论物理学家研究最基本的、最原始问题时取得的突破性研究成果，往往包含对数学发展有建设意义的、有启发作用的思想方法。杨振宁对此深有体会，数学与物理学二者的关系成为长期萦绕在他思想中的一个问题。从美学的角度，杨振宁认为：“物理学——当然包括理论物理学——中的许多美是与数学中的美的观念紧密相关的。”^[1] 但就具体内容而言，他更强调二者之间大异小同的事实。1979 年他对此作了较为明确的描述。^[2]在他看来，数学和物理学之间，除了有若干共同的最基本的概念外，一致性的东西不多；二者之间更多的是不同：目标取向不同、情感好恶不同、研究传统不同、价值观念不同、主体内容不同。深入辨析和体会不难发现，杨振宁所说的数学与物理的诸多不同，有些实质所指是数学家与物理学家之间的差异，比如不同的情感好恶等。在此之后杨振宁为进一步形象地表达他的这一认识，描绘出著名的双叶图。1980年1月在香港大学的演讲中，杨振宁借助双叶图，再次阐述他关于数理关系的观点：“在基本概念的水平上，它们令人惊异地共同使用某些概念，但即使在这里，每一方面的生命力是沿着各自的脉络奔流的（见图 1）。”^[3] 据本文作者的初步了解，这是杨振宁第一次用双叶图阐释数理关系。

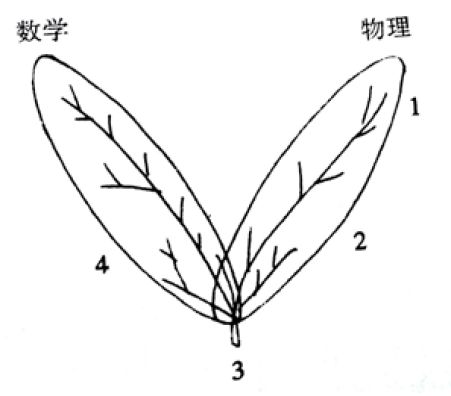
图1  1980年绘双叶图

在1997年的文章中，杨振宁仍然借助双叶图说明数理关系，并对图中双叶重叠的那一小部分，即数学与物理学相同或相似的部分，以及双叶彼此不同部分的内涵做了更深入的辨析性说明，具体指出重叠部分包括微分方程、偏微分方程、希尔伯特空间、黎曼几何和纤维丛等，但是强调物理学家和数学家达成这样的“共识”或思想融合所经过的是殊途同归的道路，而更多不是同心协作的结果。虽然这些重叠领域对于物理、对于数学都很重要，杨振宁依然相信并肯定：“重叠的地方并不多，只占二者各自的极少部分。譬如实验（1）与唯象理论（2）都不在重叠区，而绝大部分的数学工作也在重叠区之外。”（[3]，p.849）这一诠释简明扼要、清晰透彻，认为数学与物理在最早的、最原始的部分同脉同源；但是因为二者有不同目标和价值取向，在其后的发展过程中，主体发展态势是渐行渐远。

杨振宁还一贯认为，双叶图中重叠的部分不是固化的，而是随着物理学和数学的发展，双叶逐渐“长大”的同时，其重叠面积呈扩大之趋势。有理由相信，在杨振宁的思想中，这种重叠区域的变动并非仅仅是因为数学或物理学各自独立发展并跨界使然，而是数学和物理学本质上互为重要发展源动力的关系使然。在 1993 年的一篇文章中，杨振宁较为详尽地表达了这一思想：“交叠的面积只是每个学科的一小部分，或许仅有百分之几。例如，实验物理学就不在交叠的区域中，虽然它代表物理学中一大块研究领域。有时，交叠的面积会扩大，例如，当爱因斯坦将黎曼几何引入物理学时。但同时这两门学科的不交叠的面积也大大地扩张了。”（[3]，p.779）“交叠的面积”的扩大标志着物理学和数学的发展能促进二者重合部分增加，而“不交叠的面积”的“大大扩张”则代表物理学与数学在具有截然不同的取向、毫无关联的部分也有了更加长足的进步。这意味着，物理学与数学重叠部分的增加速率低于物理学与数学各自非重叠部分的发展速率。

虽然事实如杨振宁所说，数学与物理学有互相交融、彼此促进的关系，但并非所有数学家和物理学家对于二者的交融说均持支持与期待的态度，尤其一些数学家渴望着数学与物理学最好井水不犯河水。杨振宁指出数学与物理学的交融态势并不因为部分数学家的主观反感而弱化，于是就导致一种不和谐学术现象的出现：一方面，“本世纪中一大群数学家有脱离物理学的倾向”，但与此同期，科学家越来越认识到：“很难避免得出这样的结论：自然界似乎倾向于用数学中漂亮的基本结构去组织物理的宇宙。”（[3]，pp.779-780）这段话揭示了数学与物理学世界之间的密切关联是不随部分数学家的主观意愿而改变的事实，数学与物理学愈发纠缠于一起之大趋势，过去已然，现在仍然、未来还将依然如是。探寻这其中的根本奥妙，则要回到古希腊的毕达哥拉斯主义或后期的新柏拉图主义，这一思想完全蕴涵于被历代物理学家，从伽利略、牛顿、爱因斯坦到海森堡，再到杨振宁等等反复翻版的那句源自毕达哥拉斯学派的信条：万物皆数。当然他们之中没人还相信数是万物本原，但都认可和强调在认识世界过程中数学是不可或缺的重要角色。 

从方法上看，物理学家与数学家的研究与探索，在出发点即已分道扬镳：物理学家总是从现象、从实验事实开始，去假设、去构造、去预言、去验证；而数学家则从基本的公理等少数逻辑前提开始，然后按演绎法一环接一环推论下去。杨振宁讲过一个数学家打趣物理学家的故事：你们物理学家，感觉自己很厉害、了不起，但一再发现，我们数学家总是提前给你们准备好了数学工具，你们需要矢量时我们已有矢量代数；你们需要张量时，我们早已准备就绪；在你们需要矩阵的时候，我们已经准备好近百年了。而我们不需要实验室和实验设备，只靠推理和想象我们就做到了这一切。杨振宁接着这个话题说了以下一段话：

“数学家和物理学家都知道电磁场的基础结构是纤维丛结构，但数学家研究纤维丛是什么东西，这是他的着重点；物理学家也认为它妙不可言，可是物理学家着重考虑的是这个数学结构用到实际上会有什么新的发展。数学与物理重叠的部分一定是对数学家有用的物理，或对物理学家有用的数学。如果能有办法把这部分辨析、分离出来，无疑对数学家和物理学家都是很有意义的。但是这很难。怎么能找到哪部分是重叠的？我想没有方法和规律。”

他的这段话，除有对双叶图的进一步说明外，还涉及到了他的另一个观点，即人们对于数学与物理学之间关系的认识尚未结束：“数学和物理学的关系不是一个已经弄得很清楚的问题。”（[3]，p.333）他甚至认为：“数学与物理学的关系问题是个有吸引力的问题，也是个经过大量评论的问题。我并不认为对于这个关系究竟是什么的问题，会有任何具体明确的解答。”（[3]，p.332）这些表述充分展示了杨振宁对待数理关系所持有的开放与发展的眼光。

二、应用数学：数学与物理学之中介

双叶图能表达杨振宁关于数理关系的很多思想，但也并非是他在这个问题上的全部认识。他还曾通过数学的特殊分支，直接将数学和物理学联系起来，构成了数理科学在二维平面上彼此交叠的“连续谱系”，并以此阐释二者的关系。这一特殊的数学分支即应用数学。1961 年，早在提出双叶图之前的一次学术会议上，杨振宁表达了他的这一观点：

应用数学是一门大部分介于数学和物理学之间的创造性学科。但也介于数学和其他学科之间。在这一领域里，用数学语言综合物理世界的一些现象。应用数学与理论物理之间应该只有强调上的一个小区别，即强调从物理现象到数学公式的归纳与从数学公式到物理现象的演绎过程的不同而已。理论物理学家更强调归纳过程，应用数学家更强调演绎过程。一位真正好的理论物理学家实际上也应该是一位好的应用数学家，反之亦然。我相信这一观点与应用数学家的本身的观点是一致的……（[3]，p.115）

也就是说在这一视角下，杨振宁认为数学与物理学的交集构成应用数学的主体部分；以物理学家的视角看物理学与数学的这一交集部分，它就是理论物理学；而以数学家的眼光来看，它是数学中的应用数学的一大部分。如此看待数学与物理学的关系，二者之间的交集包含全部的理论物理学，这要远远大于双叶图比喻中数学与物理学的交集。用这种方法展示数学与物理学之间的关系，言外之意是对数学和物理学都采用了二分法：数学包括应用数学和非应用数学；物理学包括主要以数学为研究工具的理论物理学，以及实验物理学。此种看法更加宏观化、粗粒化，立足于数学与物理学主体方法的不同；而双叶图中对于数学与物理学叠合部分之解释，相对而言更加微观、细化，可以落实到某些具体概念。但横岭侧峰，两个视角并无对错之别，各揭示一定思想寓意，分别有不同的启发意义。

三、数学家与物理学家对待研究成果的不同感受

本文作者对杨振宁著述中的一些语汇，诸如描述数学家或物理学家时所用的专业“情趣”与“爱憎”等等颇感兴趣，曾就此请其予以说明。在对这一话题的阐述中，杨振宁先生的一些观点相当独到。

“我用‘情趣’一词形容数学家和物理学家，是一种没有办法的借用。科学家与艺术家的工作有什么不同呢？我想最主要的是一个和情感有关，一个和情感无关。理论物理学家和数学家的感受到底有什么分别呢？这其实是个很重要的题目，我思考过，但还没有写出来。我认为，真正到了非常重要的革命性的新发展阶段，面对自己的成果，数学家和物理学家的感受有一个很大的不同，那就是数学家的感受是无我的，而物理学家的感受是有我的。数学家的研究结论总属于数学家个人之外的世界，而不是关于他自己的。物理学家却与此不同。麦克斯韦写下麦克斯韦方程组，他据此算出电磁波的速度和光速是一样的，于是他指出光就是电磁波。我对此是非常佩服的。^[4]物理学家做出的很多重要发现里是有‘我’的，物理学家在做出重大发现的时候，他不能忘记他本身也是受这个规律支配的。所以面对最重大的新发现的时候，物理学家和数学家在感受上是否有‘我’这个问题上，答案是截然不同的。” 

数学家与物理学家作为个体人都是矗立于数学世界与物理世界面前的镜子，其心理感受的不同，是由于物理学与数学分别描述自然界不同层面从而产生的区别，物理学的内容不能超越对现实物质世界的描写与解读，但是数学世界可以更加宽广。

四、理论物理学家的数学知识多多益善么？

物理学家尤其理论物理学家，离开数学会束手无策。在特殊时刻理论物理学家毫不隐晦他们对于更多数学知识的渴求。如薛定谔在尝试建立描述量子现象的薛定谔方程时,就曾发出这样的感慨:“此刻我正在为建立新的原子理论而挣扎。如果我拥有更多的数学知识有多好！……现在，为了彻底结束对于振动问题的研究，我必须学习更多线性微分方程方面的知识，它与贝塞尔方程相似，但并不广为人知。”^[5]那么一位理论物理学家是否可以通过先学习更多的数学来增加自己作为理论物理学家的优势呢？杨振宁结合自身的体会和观察，对此的态度是明确否定的：过多学习和涉猎数学的理论物理学家，有可能丧失自己的物理直觉能力。（[3]，p.740）而在这一问题的另一方面，杨振宁指出：数学家接受较多的物理学的训练，对于他其后吸收数学概念却不是障碍，恰恰相反，“实际上，它往往有助于进行创造性的数学思维。为什么会这样，显然是一个深奥的问题。”（[3]，p.115）在与本文作者的谈话中，杨振宁再次强调了过分喜爱和学习数学，会成为物理学家增强本专业研究能力的障碍：“数学的美是非常诱人的。数学研究的这种引诱可以达到不拔之境的地步。假如想要研究物理的话，不能被数学引诱得太厉害。数学引诱太厉害的话，研究物理的想法就会被撇开了。”

物理训练不影响进一步接受数学，但是过多数学熏陶可以使学习物理的人转行成为数学家。为什么这样？杨振宁说这“是一个深奥的问题”，却并未予以进一步解答。我们可以从两个方面予以理解。其一是杨振宁所说的，数学与物理，有不同的价值、不同的趣味与不同的传统，对于极少的特殊者而言二者可以兼得、可以相得益彰，但是对于多数人而言鱼与熊掌不可兼得。一个人如果想致力于物理学研究，那么要有意识提醒自己，有意识控制自己的数学爱好，否则过多地沉醉于数学之中，完全有可能造成物理研究之树上生长能力的削弱或顶端优势的丧失。其二，数学世界大于物理世界，数学世界中涵盖现实世界那一部分，就是物理世界；而数学世界中靠想象与逻辑推理超越现实世界的部分，则是不允许在物理学存在的。年轻时的爱因斯坦曾有这样的感受：“数学分成许多专门的领域，每一个领域都能费去我们所能有的短暂的一生。”^[6]庞大的数学风景区会让有的人自我迷失而走不出来，也可能让有的人乐不思蜀而不再想走出数学世界。 

有志于成为物理学家的年轻人，更多的还是要培养自己的物理直觉，当然也不是不需要基本的数学素养，但想一劳永逸先学好将来物理研究中能用到的数学的念头并非切实可行。理论物理学更多的成功之士，从爱因斯坦到薛定谔等，在研究物理学特殊问题过程中，遇到自己难以解决的数学困难时，都是通过向周围数学能力更好的人请教并得到指点而攻克科研难关的。因此理论物理学家结交几位有能力的数学家朋友，似乎比自己盲目地追求储备过多数学知识更加必要。这与杨振宁的观点是相合的。

五、杨振宁与爱因斯坦对数学的相似感悟

爱因斯坦借助黎曼几何建立了广义相对论。这一经历使他对数学有了更深刻的感悟和困惑：数学是与经验无关的人类思维产物，为什么它在描述自然界方面如此异常重要？基于这样的思考，1921 年爱因斯坦曾提出如下问题“是不是不要经验而只靠思维，人类的理性就能够推测到实在事物的性质呢？”（[6]，p.136）这第二个问题不可小视，提出这一问题，一定意义上意味着对于物理学实验纲领的怀疑，甚至显露了背叛这一物理学基本纲领的思想意识。相信有一些理论物理学家会对爱因斯坦在这里提出的第二个问题给出否定答案，爱因斯坦本人更多时候也是这样做的，但是无可否认数学具有的这种超然的强大功能，的确曾让爱因斯坦费解、困惑并对此展开深思。 

爱因斯坦在建立广义相对论之前其数学积淀以及对于数学的认识都有欠缺。对此他是直言不讳的。比较而言，数学在杨振宁的知识世界里较早就占据至少与物理学同样重要的地位。杨振宁欣赏并钦佩数学的趣味、数学的美感与数学的力量，同时像爱因斯坦一样，数学不可思议的作用也令他震惊与讶异：“我的大多数物理学同事都对数学采取一种功利主义的态度。或许因为受父亲的影响，我比较欣赏数学。我欣赏数学的价值观念，我钦佩数学的美和力量；在谋略上，它充满了巧妙和纷杂；而在战略战役上则充满惊人的曲折。除此之外，最令人不可思议的是，数学的某些概念原来竟规定了统治物理世界的那些基本结构。”（[3]，p.214）这种“不可思议”、这种震惊与讶异不是来自于抽象的意向或朦胧的感觉，而是源自于十分具体的直接感悟。杨振宁成功利用数学的纤维丛理论建立了物理学领域异常重要的规范场理论，二者完美的契合令他惊叹、叹服。对此他曾与数学家陈省身有过交流：“1975年我与陈省身讨论我的感觉，我说：‘这真是令人震惊和迷惑不解，因为不知道你们数学家从什么地方凭空想象出这些概念（指纤维丛）。’”（[3]，p.242）不难看出，对于数学魔力直接的亲身感受和疑惑在爱因斯坦和杨振宁的思想世界里是极为相似的。

杨振宁与爱因斯坦对于数学的相似感悟还有很多。读书时对数学怀着敬而远之心理的爱因斯坦，后来数学在他的思想中的分量却与日俱增。他甚至认为在所有的科学学科中，数学具有无可比拟的特殊性与权威性。让他产生并坚信这一认识的理由之一是，在他看来，物理、化学等其他自然科学，存在无休止的优胜劣汰、改朝换代或新陈代谢；但数学世界一经奠定即江山永固，与物理世界存在着根本的不同：“为什么数学比其他一切科学受到特殊的尊重，一个理由是它的命题是绝对可靠的和无可争辩的，而其他一切科学的命题在某种程度上都是可争辩的，并且经常处于会被新发现的事实推翻的危险之中。”（[6]，p.136）无独有偶，在杨振宁与本文作者的交谈中，他将物理学与数学相比较，曾详尽地表达了与爱因斯坦的这一看法十分一致的认识。

“数学这门学科像是一座极其漂亮的宏大的宫殿，里面漂亮的东西有很多。代数、几何等不同的分支都有其妙处，而且妙的地方又互相关联起来。……一个数学家假如发现或证明了一个很漂亮的定理，那么他这个功劳永远存在，不会消失或被推翻。数学世界没有淘汰机制，微小的创造也永远不朽而足以令其创造者自豪。相反在物理学界就不一样。随着老一代物理学家的理论被后来者所淘汰，他们也就失去了在物理学中的重要性，因而在物理界将逐渐淡出后人的视野。从长远的角度来看做数学比较保险。亚里士多德的很多物理学结论都是错误的，但数学领域比他更早的毕达哥拉斯定理却永远正确。从这个立场讲，物理和数学的价值观是不一样的，历史境遇也是彼此不同的。”  ①

关于物理学与数学之间的复杂关系，杨振宁在著述中多次表达自己的看法，他不否认这是一个尚未讨论清楚甚至可能永远没有明确答案的问题。在杨振宁关于数学与物理关系的所有论述中，有一种积极乐观看待事物与事物发展的心态。展望未来，他坚信物理学与数学必将继续互相纠缠、互相渗透并互相促进：“我个人相信，在下一个世纪，（数学与物理学）交叠区域将继续扩大，这对两门学科都会有益。”（[3]，p.780）

[参 考 文 献]

[1]杨振宁. 美和物理学[J]. 自然辩证法通讯, 1988, 10（1）: 1-7.

[2]杨振宁. 曙光集[M]. 翁帆编译, 北京: 生活·读书·新知三联书店, 2008, 17.

[3] 杨振宁. 杨振宁文集[M]. 上海: 华东师范大学出版社, 2000, 334.

[4]Chen, N. Y. 'The Conceptual Origins of axwell’s Equations and Gauge Theory'[J]. Physics Today, 2014, 67(11): 45-51.

[5]Moore, W. A Life of Erwin Schrödinger[M]. Cambridge: Cambridge University Press, 1994, 141.

[6]爱因斯坦. 爱因斯坦文集[M]. 许良英、范岱年编译, 第一卷, 北京: 商务印书馆, 1976, 7.

————

编辑 ∑Pluto

来源：ET创芯网

更多精彩：

☞泰勒定理的奇闻轶事

☞丘成桐：漫谈微分几何

☞Leibniz 如何想出微积分？（一）

☞线性相关和秩的物理意义

☞数学史上你认为最丑陋的公式是什么？

☞陶哲轩谈什么是好的数学

☞田渊栋：数学的用处（下篇）

☞你绝对没想过原来数学家这么流氓，一言不合就进行暴力证明

☞世界上最牛的五篇博士论文

☞数学中有哪些巧合让人眼前一亮？

☞算法立功！清华毕业教授美国被抢车，警察无能为力自己用“贪心算法”找回

☞学术史上的奇文：怎样用数学抓狮子

☞台大教授的反思：最难的一课 我们却没教给学生

☞麻省理工学院(MIT)研究生学习指导—— 怎样做研究生

☞分享 数学，常识和运气 ——投资大师詹姆斯·西蒙斯2010年在MIT的讲座

算法数学之美微信公众号欢迎赐稿

稿件涉及数学、物理、算法、计算机、编程等相关领域，经采用我们将奉上稿酬。

投稿邮箱：[email protected]