网络流入门教程之最大流(DINIC/EK)
网络流入门教程之最大流
一.引入
生活中有很多东西很像网络流。
我们想象一下自来水厂(假设自来水厂水量无限)到你家的水管网是一个复杂的有向图,每一节水管都有一个最大承载流量。自来水厂不放水,你家就断水了。但是就算自来水厂拼命的往管网里面注水,你家收到的水流量也是上限(毕竟每根水管承载量有限)。你想知道你能够拿到多少水,这就是一种网络流问题。
同样的假设s城有无限个人想去t城,但是从s到t要经过一些城市才能到达,其中s到x城的火车票还剩20张,x到t的火车票还剩10张,其他路以此类推,问最终最多能有多少人能到达t城?
先从最基础的最大流开始:
最大流问题是想让我们解决什么问题?
形象的说就是有一段水流从源点s经过很多路径,路径有一个流量上限lim,即最多只有lim那么多的水能够通过这条路径。询问最终能有多少水到达汇点t。
结合图片进行解说:
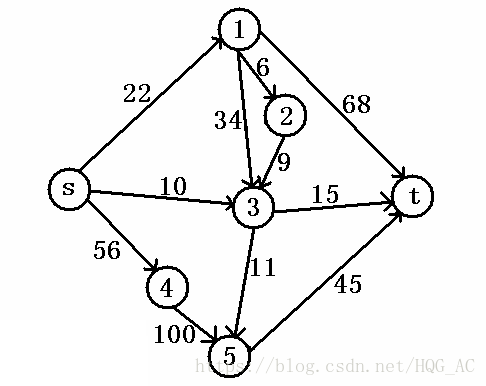
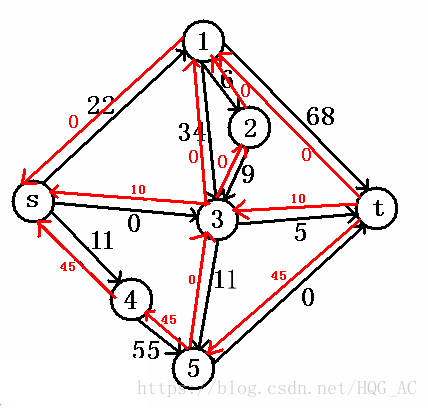
下面是一个有向图,s和t已经在图中标出
途中路径的流量已经标出,易知改图的最大流=10+22+45=77。
那么这个问题该真么解决呢?
我们发现,制约我们最大流大小的就是那些流量非常的少的水管(就这么说吧 )。
于是我们可以找到哪些流量非常少的水管,再进行操作。
我们先从比较简单的EK说起
二.EK算法
EK算法全称Edmond—Karp(不要问我为什么那么高级 )
首先说一些定义:
- 源点:只有流出去的点
- 汇点:只有流进来的点
- 流量:一条边上流过的流量
- 容量:一条边上可供流过的最大流量
增广路 : 从s到t的一条路,流过这条路,使得当前的流可以增加。其实就是最大流还有可以上升的空间。
通过增广路的定义,我们发现最大流问题可以转换成为求解增广路问题,如果图中没有了增广路必然没有最大流。
操作过程如下:
从s开始广搜,走权值大于0的边,知道走到t。在此同时我们要记录每个节点是从哪里走来的。之后我们找到最小的边权x,使得每一条边的权值-x。当我们找不到增广路时退出。
在累加最大流的时候,为了防止重复加某一段,我们要对每一条边减掉最大流。
给一下增广路的代码:
struct node {
int x, id ;//前面的点,边的编号
} pre[N] ;
bool bfs() { //找增广路
queue <int> q ;
memset(inque, 0, sizeof(inque)) ;
memset(pre, -1, sizeof(pre)) ;
inque[s] = 1;
q.push(s) ;
while (!q.empty()) {
int now = q.front() ;
q.pop() ;
for (int i = head[now]; i; i = e[i].nxt) {
int to = e[i].to ;
if (!inque[to] && e[i].w) { //流过去
pre[to] = (node) {now, i} ; //从哪个点流过来
if (to == t) return 1 ;//找到
inque[to] = 1 ;
q.push(to) ;
}
}
}
return 0 ;//没找到
}
累加最大流:
int EK(){
int ans = 0 ;
while (bfs()) {
int MI = iinf ;
for (int i = t; i != s; i = pre[i].x) MI = min(MI, e[pre[i].id].w) ;
for (int i = t; i != s; i = pre[i].x) e[pre[i].id].w -= MI ;
ans += MI ;
}
return ans ;
}
WA了。(一脸懵逼的看着 )
万一第一次流错了使得这样的流法无法得到最大流怎么办?
哦对啊。
依然是这张图
如果你第一次的增广路是:s->3->5->t最大流显然是10,第二次的增广路是s->4->5->t最大流显然是35(因为5->t的最大流有10点被3号点来的人占领了)。
而这种方案显然不如:s->4->5->t最大流为45,s->3->t最大流为10。
那么怎么最优? 建反向边。
为什么要建反向边?占空间?占时间? 当然不是哈哈哈 。
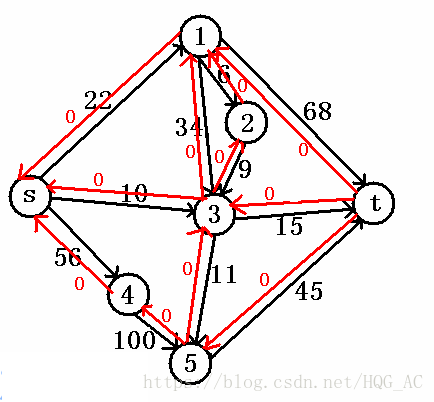
先找增广路,比如说我们走了s->3->5->t,那么图会变成:
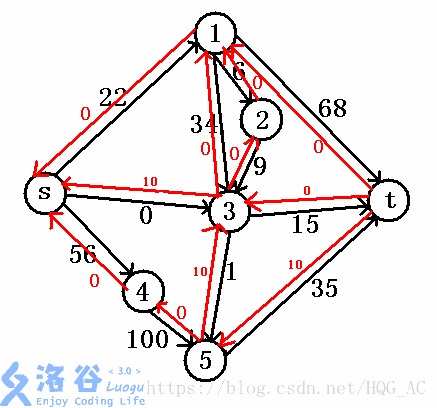
再找一次增广路,这次比如说我们走s->4->5->t。
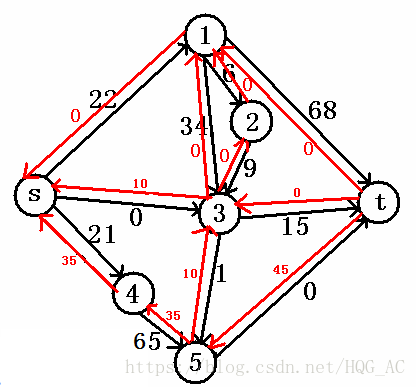
再找一次增广路,这次我们找s->4->5->3->t
为什么这次搜索的时候走了反向边(红色)的边,为什么走了反向边(红色)的边会加正向边(黑色)的边?
这就好像是45个人沿着s->4->5->t的路线想去t城,到了5城却发现有10个来自3城的人先定了5->t的票!他们十分焦急,总不能让他们在5城等吧。
怎么办呢?他们通过反向边上的标记发现了那10个人是来自3城的,利用标记,他们发现那10个人可以直接从3城到t城,于是他们告诉还在3城时的那10个人可以直接走3->t这条路,然后他们就可以买到空出来的5->t的10张票了。
于是你知道了:反向边的作用就是反悔,能够让前面的人走回头路。
理解了反向边的作用,恭喜你已经理解了EK求解最大流算法的原理了。
大家有学过桥(双连通分量)么?
里面判断两条边互为反向边的操作是什么?
x -> x ^ 1
于是这个也可以这么判断
还有一件事情,建边时要从2开始建,否则会wa的
给一下EK的代码:
【模板】网络最大流
#include
#include 但是,某位洛谷大佬曾说:根据相关法律法规,网络流题不允许卡Dinic/ISAP,但可以卡EK,数据应严格遵循上述条约。
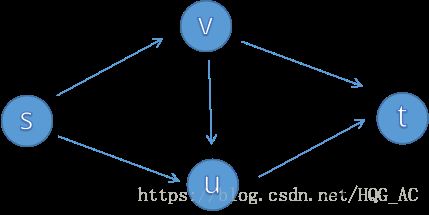
EK算法常被称为网络流的朴素算法,因为他在一些毒瘤 数据下的运行时间并不理想,比如:
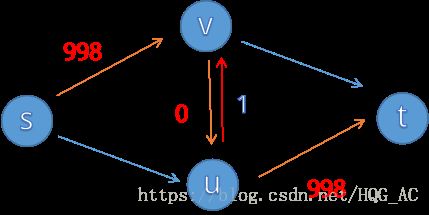
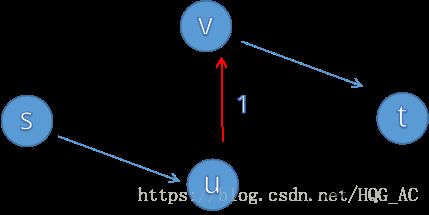
我们一眼可以看出最大流是999(s->v->t)+999(s->u->t),但如果程序采取了不恰当的增广策略:s->v->u->t
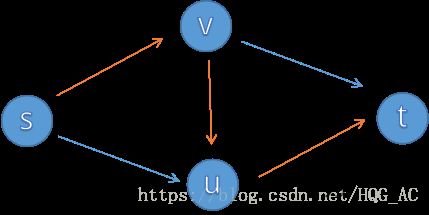
我们发现中间会加一条u->v的边
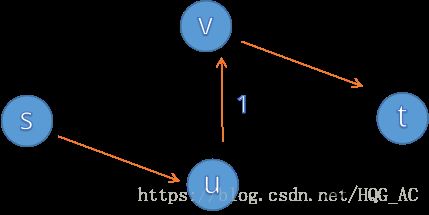
而下一次增广时:
若选择了s->u->v->t
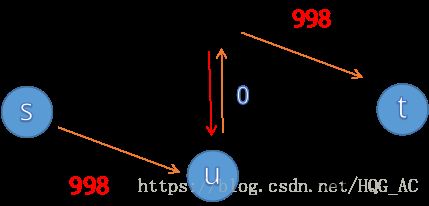
然后就变成
这是个非常低效的过程,并且当图中的999变成更大的数时,这个劣势还会更加明显。
怎么办呢?
这时我们引入Dinic算法
三. DINIC算法
为了解决我们上面遇到的低效方法,Dinic算法引入了一个叫做分层图的概念。
具体就是对于每一个点,我们根据从源点开始的bfs序列,为每一个点分配一个深度,然后我们进行若干遍dfs寻找增广路,每一次由u推出v必须保证v的深度必须是u的深度+1。
bfs分层图过程
bool bfs() { //分层图
queue <int> q ;
q.push(s) ;
clr(dep) ;
dep[s] = 1 ;
while (!q.empty()) {
int now = q.front() ;
q.pop() ;
for (int i = head[now]; i; i = e[i].nxt) {
int to = e[i].to ;
if (e[i].w && !dep[to]) {
dep[to] = dep[now] + 1 ;//更新深度
q.push(to) ;
}
}
}
if (!dep[t]) return 0 ;//没有从s到t的增广路
else return 1 ;
}
dfs寻找增广路过程
int dfs(int rt, int dis) {
if (rt == t) return dis ;
for (int i = head[rt]; i; i = e[i].nxt) {
int to = e[i].to ;
if (dep[to] == dep[rt] + 1 && e[i].w) { // 是在下一层
int p = dfs(to, min(dis, e[i].w)) ;
if (p) { //可流
e[i].w -= p ;//更新
e[i ^ 1].w += p ;
return p ;
}
}
}
return 0 ;//没找到增广路
}
主函数
int Dinic() {
int ans = 0 ;
while (bfs()) { //有增广路
while (int d = dfs(s, iinf)) ans += d ;//找
}
return ans ;
}
最后发一下全部代码,同样还是那道叫做网络最大流的题目
#include
#include 作业:
- 草地排水
- 飞行员配对方案问题 (二分图匹配)
- 魔术球问题
thanks for your reading!