邻接矩阵与关联矩阵

【邻接矩阵】

定义：
设无向图 G=(V,E) G = ( V , E ) ,其中顶点集 V=v1,v2,...,vn V = v 1 , v 2 , . . . , v n ，边集 E=e1,e2,...,eε E = e 1 , e 2 , . . . , e ε 。用 aij a i j 表示顶点 vi v i 与顶点 vj v j 之间的边数，可能取值为0,1,2,…，称所得矩阵 A=A(G)=(aij)n×n A = A ( G ) = ( a i j ) n × n 为图G的邻接矩阵

若干性质

• A(G) A ( G ) 为对称矩阵
• 若G为无环图，则 A(G) A ( G ) 中第i行（列）的元素之和等于顶点 vi v i 的度
• 两图G和H同构的充要条件是存在置换矩阵P使得 A(G)=PTA(H)P A ( G ) = P T A ( H ) P

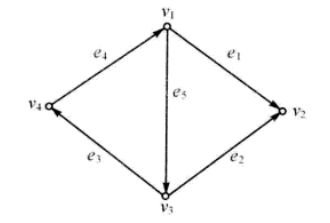
类似地，有向图D的邻接矩阵 A(D)=(aij)n×n A ( D ) = ( a i j ) n × n , aij a i j 表示从始点 vi v i 到终点 vj v j 的有向边的条数，其中 vi v i 和 vj v j 为D的顶点

示例，求图所示简单图的邻接矩阵？

解：根据定义，可求得该无向图的邻接矩阵为

⎡⎣⎢⎢⎢0111101011011010⎤⎦⎥⎥⎥ [ 0 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 ]

注：邻接矩阵是描述图的一种常用的矩阵表示。

【关联矩阵】

定义：
设任意图 G=(V,E) G = ( V , E ) ，其中顶点集 V=v1,v2,...,vn V = v 1 , v 2 , . . . , v n ，边集 E=e1,e2,...,eε E = e 1 , e 2 , . . . , e ε 。用 mij m i j 表示顶点 vi v i 与边 ej e j 关联的次数，可能取值为0,1,2,…，称所得矩阵 M(G)=(mij)n×ε M ( G ) = ( m i j ) n × ε 为图G的关联矩阵

类似地，有向图 D D 的关联矩阵 M(D)=(mij)n×ε M ( D ) = ( m i j ) n × ε 的元素 mi×j m i × j 定义为：

mij=⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪1,−1,0,vi是有向边aj的始点vi是有向边aj的终点vi是有向边aj的不关联点 m i j = { 1 , v i 是 有 向 边 a j 的 始 点 − 1 , v i 是 有 向 边 a j 的 终 点 0 , v i 是 有 向 边 a j 的 不 关 联 点

示例，求图中有向图的邻接矩阵和关联矩阵。

解：根据定义，可求得该有向图的邻接矩阵:

⎡⎣⎢⎢⎢0001101010000010⎤⎦⎥⎥⎥ [ 0 1 1 0 0 0 0 0 0 1 0 1 1 0 0 0 ]

关联矩阵:

⎡⎣⎢⎢⎢1−1000−110001−1−100110−10⎤⎦⎥⎥⎥ [ 1 0 0 − 1 1 − 1 − 1 0 0 0 0 1 1 0 − 1 0 0 − 1 1 0 ]

注：关联矩阵是描述图的另一种矩阵表示。