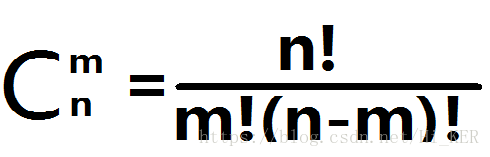关于组合数求值--枚举+分析

组合数的求值公式：

这个公式看起来有点复杂，如果知道C(n,m)的值我们该怎么求m,n的值呢？

看下面这道例题：

题目：

二项式系数

Description

　　二项式定理（英语：Binomial theorem），又称牛顿二项式定理，由艾萨克•牛顿于1664年、1665年期间提出。该定理给出两个数之和的整数次幂诸如 展开为类似 项之和的恒等式。二项式定理可以推广到任意实数次幂，即广义二项式定理。二项式定理可以用以下公式表示：
　　　
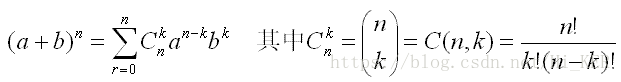
　　我们称C(n,k)为二项式系数。

　　现在，你要解决得问题是：已知某二项数系数为m，那么有多少个(n,k)满足(C(n,k)=m，按照n升序排列，若n相同，则按k升序排列。

Input

　　第一行为整数T，表示数据组数。接下来的T行，每组数据占一行，为一个整数m。

Output

　　每组数据输出两行，第一行为满足条件的(n,k)的数，接下来一行为满足条件的(n,k)对，每队用括号括起来，括号之间用一个空格分开。按n升序排列，若n相同，则按k升序排列。

Sample Input 1 

2
2
15

Sample Output 1

1
(2,1)
4
(6,2) (6,4) (15,1) (15,14)

Hint

2<=m<=10^15

分析：

m<=10^15,枚举肯定不现实，我们知道C(n,1)=n;C(n,2)=n*(n-1)/2，我们从C(n,2)开始枚举那么就只需要sqrt(m),的时间就可以枚举完，同理C(n,3)=n*(n-1)*(n-2)/6,令m=C(n,3),解得m≈cuberoot(6*m),(cuberoot，即三次根号下)由计算器算得m≈182000

这样，我们从n=1预处理到n=182000中C(n,k)<=max_m的n,k的值存入hash表,每次输入m,我们先在hash表查找C(n,k)=m的n,k在特判C(n,1)=m和C(n,2)=m的情况就可以了

时间复杂度：约为：O(k*cuberoot(6*m)+k*ans)  //ans含义见代码

实测时间：

OJ1:十个测试点，平均700ms每个

OJ2:十个测试点，平均200ms每个

代码：

#include
using namespace std;
#define ll long long
const int SZ=189997;
const ll RNG=1000000000000000LL;
int I;
struct node{
	ll v;
	int n,m;
	node* next;
	node():next(NULL){}
};
node* rt[SZ];
void add(ll v,int n,int m){
	I=int(v%SZ);
	if(rt[I]==NULL){
		rt[I]=new node;rt[I]->v=v;
		rt[I]->n=n,rt[I]->m=m;return;
	}
	node* P=rt[I];
	while(P->next!=NULL) P=P->next;
	P=P->next=new node;
	P->v=v,P->n=n,P->m=m;
}
int n[SZ],m[SZ],sz_nm;
void find(ll v){
	I=int(v%SZ);
	node* P=rt[I];
	while(P!=NULL){
		if(P->v==v){
			n[++sz_nm]=P->n;
			m[sz_nm]=P->m;
		}
		P=P->next;
	}
}
void ready(){
	ll T;
	for(int i=2;i=SZ&&T*(T+1)==2*M) ans+=2;//特判n==2
	ans+=2;
	out:
	printf("%d\n",ans);
	for(int i=1;i<=sz_nm;i++){
		printf("(%d,%d) ",n[i],m[i]);
		if(n[i]!=m[i]*2) printf("(%d,%d) ",n[i],n[i]-m[i]);
	}
	if(M<(ll)SZ){printf("\n");return;}
	if(T>=SZ&&T*(T+1)==2*M) printf("(%lld,%d) (%lld,%lld) ",T+1,2,T+1,T-1);
	printf("(%lld,%d) (%lld,%lld)\n",M,1,M,M-1);//n==1的情况 
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int T;
	ll m;
	ready();//预处理 
	scanf("%d",&T);
	while(T--){
		scanf("%lld",&m);
		solve(m);
	}
}

方法2：

因为C(n,k)的值当k从1开始增加时增很快，我们可以枚举k,然后根据范围(二分)查找n可能的值，然后排序输出即可