HDU - 1695 GCD 莫比乌斯反演

题目链接
题意：

给你 a , b , c , d , k 五个值 （题目说明了 你可以认为 a=c=1） x 属于 [1,b] ，y属于[1,d] 让你求有多少对这样的 （x,y）满足gcd（x,y）==k。给你的时间是 3000 MS。 0 < a <= b <= 100,000, 0 < c <= d <= 100,000, 0 <= k <= 100,000

思路：

mobius反演入门题.
首先介绍一下mobius反演的两种形式:

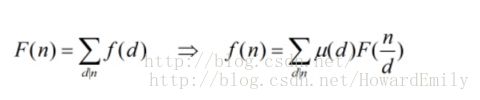
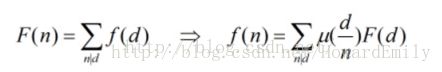
首先我们根据gcd的性质把式子改写一下 gcd(x,y) =k 等价于gcd（x/k,y/k）=1。
转化到这里之后,我们要用到mobius的第二种形式.
设F（d） 表示gcd(x,y) = d的倍数的对数.
f(d) 表示gcd（x,y） =d的对数.
显然F(d)很好求 就是 nd∗md
那么由第二种反演的
f(n)=∑n|du(dn)∗F(d)
我们要求gcd为1的所以就是n=1,结果为 f(1)=∑n|du(d)∗F(d)

因为题目中说(1,2)和（2,1）算同一个,所以我们的计算会有重复的,
我们设n < m，那么只有区间同在（1，n）范围内的才会重复,所以我们去掉这一部分的答案即可.
设在（1，n）和（1，m）的答案为ans1,在(1,n)和（1，n）的为ans2,答案就是ans1-\frac{ans2}{2} $

先附上mobius函数两种求法
第一种 普通筛选求莫比乌斯函数 时间复杂度为 O（nlogn）

void getMu(){  
    int N=maxn;  
    for(int i=1;iint target=i==1?1:0;  
        int delta=target-mu[i];  
        mu[i]=delta;  
        for(int j=2*i;j

第二种 线性筛选求莫比乌斯函数 时间复杂度为 O（n）

void Init(){  
    int N=maxn;  
    memset(prime,0,sizeof(prime));  
    memset(mu,0,sizeof(mu));  
    memset(vis,0,sizeof(vis));  
    mu[1] = 1;  
    cnt = 0;  
    for(int i=2; iif(!vis[i]){  
            prime[cnt++] = i;  
            mu[i] = -1;  
        }  
        for(int j=0; j1;  
            if(i%prime[j]) mu[i*prime[j]] = -mu[i];  
            else{  
                mu[i*prime[j]] = 0;  
                break;  
            }  
        }  
    }  
}  

ac代码

#include


using namespace std;
const int maxn = 1e5+5;
typedef long long ll;
int a,b,c,d,k;
int prime[maxn],mu[maxn];
bool vis[maxn];
void mobius()
{
    int cnt = 0;
    mu[1] = 1;
    for(int i =2;i < maxn;++i)
    {
        if(!vis[i])
        prime[++cnt] = i,mu[i] = -1;
        for(int j = 1;prime[j]*i < maxn;++j)
        {
            vis[i*prime[j]] = 1;
            if(i%prime[j] == 0)
            {
                mu[i*prime[j]] = 0;
                break;
            }
            mu[i*prime[j]] = -mu[i];
        }
    }
    return ;
}
int main()
{
    int _,ca = 1;
    cin>>_;
    mobius();
    while(_--)
    {
            scanf("%d %d %d %d %d",&a,&b,&c,&d,&k);
            if(k == 0)
            {
                printf("Case %d: 0\n",ca++);
                continue;
            } 
            ll ans1 = 0,ans2 = 0;
            b /= k,d /= k;
            int mi = min(b,d);
            for(int i = 1;i <= mi;++i)
            {
                ans1 += (ll) mu[i]*(b/i)*(d/i);
                ans2 += (ll) mu[i]*(mi/i)*(mi/i);
            }
            printf("Case %d: %lld\n",ca++,ans1-ans2/2);
    }
    return 0;
}