SuperPoint:深度学习特征点+描述子
【原文链接】:https://www.vincentqin.tech/posts/superpoint/
本文出自近几年备受瞩目的创业公司MagicLeap,发表在CVPR 2018,一作Daniel DeTone,[paper],[slides],[code]。
这篇文章设计了一种自监督网络框架,能够同时提取特征点的位置以及描述子。相比于patch-based方法,本文提出的算法能够在原始图像提取到像素级精度的特征点的位置及其描述子。
本文提出了一种单映性适应(Homographic Adaptation)的策略以增强特征点的复检率以及跨域的实用性(这里跨域指的是synthetic-to-real的能力,网络模型在虚拟数据集上训练完成,同样也可以在真实场景下表现优异的能力)。
介绍
诸多应用(诸如SLAM/SfM/相机标定/立体匹配)的首要一步就是特征点提取,这里的特征点指的是能够在不同光照&不同视角下都能够稳定且可重复检测的2D图像点位置。
基于CNN的算法几乎在以图像作为输入的所有领域表现出相比于人类特征工程更加优秀的表达能力。目前已经有一些工作做类似的任务,例如人体位姿估计,目标检测以及室内布局估计等。这些算法以通常以大量的人工标注作为GT,这些精心设计的网络用来训练以得到人体上的角点,例如嘴唇的边缘点亦或人体的关节点,但是这里的问题是这里的点实际是ill-defined(我的理解是,这些点有可能是特征点,但仅仅是一个大概的位置,是特征点的子集,并没有真正的把特征点的概念定义清楚)。
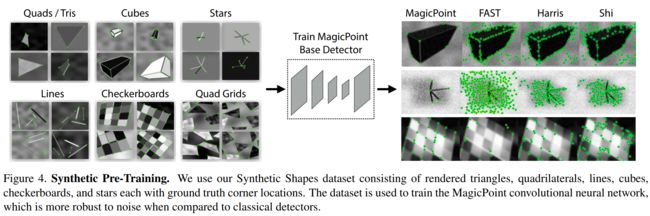
本文采用了非人工监督的方法提取真实场景的特征点。本文设计了一个由特征点检测器监督的具有伪真值数据集,而非是大量的人工标记。为了得到伪真值,本文首先在大量的虚拟数据集上训练了一个全卷积网络(FCNN),这些虚拟数据集由一些基本图形组成,例如有线段、三角形、矩形和立方体等,这些基本图形具有没有争议的特征点位置,文中称这些特征点为MagicPoint,这个pre-trained的检测器就是MagicPoint检测器。这些MagicPoint在虚拟场景的中检测特征点的性能明显优于传统方式,但是在真实的复杂场景中表现不佳,此时作者提出了一种多尺度多变换的方法Homographic Adaptation。对于输入图像而言,Homographic Adaptation通过对图像进行多次不同的尺度/角度变换来帮助网络能够在不同视角不同尺度观测到特征点。
综上:SuperPoint = MagicPoint+Homographic Adaptation
算法优劣对比
- 基于图像块的算法导致特征点位置精度不够准确;
- 特征点与描述子分开进行训练导致运算资源的浪费,网络不够精简,实时性不足;或者仅仅训练特征点或者描述子的一种,不能用同一个网络进行联合训练;
网络结构
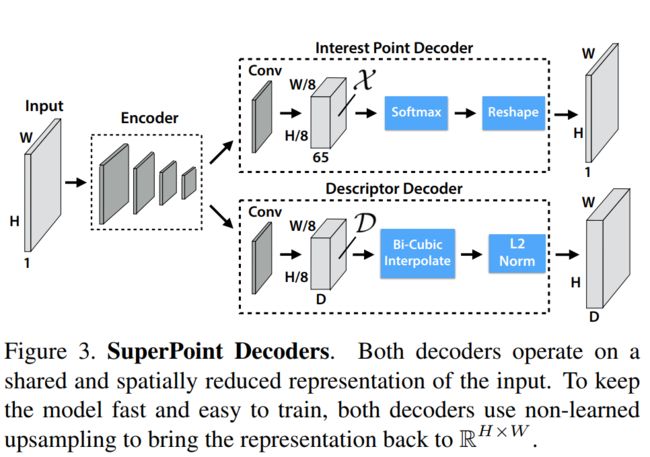
上图可见特征点检测器以及描述子网络共享一个单一的前向encoder,只是在decoder时采用了不同的结构,根据任务的不同学习不同的网络参数。这也是本框架与其他网络的不同之处:其他网络采用的是先训练好特征点检测网络,然后再去进行对特征点描述网络进行训练。
网络共分成以下4个主要部分,在此进行详述:
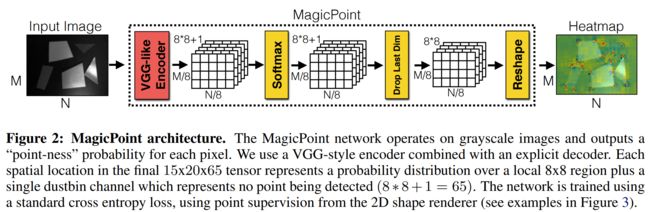
1. Shared Encoder 共享的编码网络
从上图可以看到,整体而言,本质上有两个网络,只是前半部分共享了一部分而已。本文利用了VGG-style的encoder以用于降低图像尺寸,encoder包括卷积层,max-pooling层,以及非线性激活层。通过3个max-pooling层将图像的尺寸变成 H c = H / 8 H_c = H/8 Hc=H/8和 H c = H / 8 H_c = H/8 Hc=H/8,经过encoder之后,图像由 I ∈ R H × W I \in \mathcal{R}^{H \times W} I∈RH×W变为张量 B ∈ R H c × W c × F \mathcal{B} \in \mathbb{R}^{H_c \times W_c \times F} B∈RHc×Wc×F
2. Interest Point Decoder
这里介绍的是特征点的解码端。每个像素的经过该解码器的输出是该像素是特征点的概率(probability of “point-ness”)。
通常而言,我们可以通过反卷积得到上采样的图像,但是这种操作会导致计算量的骤增以及会引入一种“checkerboard artifacts”。因此本文设计了一种带有“特定解码器”(这种解码器没有参数)的特征点检测头以减小模型计算量(子像素卷积)。
例如:输入张量的维度是 R H c × W c × 65 \mathbb{R}^{H_c \times W_c \times 65} RHc×Wc×65,输出维度 R H × W \mathbb{R}^{H \times W} RH×W,即图像的尺寸。这里的65表示原图 8 × 8 8 \times 8 8×8的局部区域,加上一个非特征点dustbin。通过在channel维度上做softmax,非特征点dustbin会被删除,同时会做一步图像的reshape: R H c × W c × 64 ⇒ R H × W \mathbb{R}^{H_c \times W_c \times 64} \Rightarrow \mathbb{R}^{H \times W} RHc×Wc×64⇒RH×W 。(这就是**子像素卷积**的意思,俗称像素洗牌)
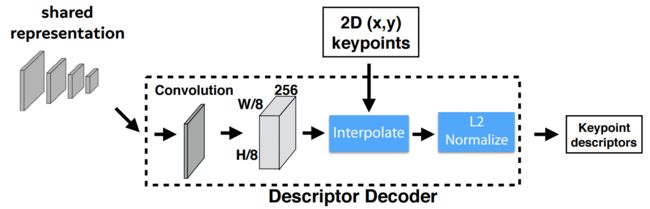
3. Descriptor Decoder
首先利用类似于UCN的网络得到一个半稠密的描述子(此处参考文献UCN),这样可以减少算法训练内存开销同时减少算法运行时间。之后通过双三次多项式插值得到其余描述,然后通过L2-normalizes归一化描述子得到统一的长度描述。特征维度由 D ∈ R H c × W c × D \mathcal{D} \in \mathbb{R}^{H_c \times W_c \times D} D∈RHc×Wc×D变为 R H × W × D \mathbb{R}^{H\times W \times D} RH×W×D 。
4. 误差构建
L ( X , χ ′ , D , D ′ ; Y , Y ′ , S ) = L p ( X , Y ) + L p ( X ′ , Y ′ ) + λ L d ( D , D ′ , S ) \begin{array}{l}{\mathcal{L}\left(\mathcal{X}, \chi^{\prime}, \mathcal{D}, \mathcal{D}^{\prime} ; Y, Y^{\prime}, S\right)=} \\ {\qquad \mathcal{L}_{p}(\mathcal{X}, Y)+\mathcal{L}_{p}\left(\mathcal{X}^{\prime}, Y^{\prime}\right)+\lambda \mathcal{L}_{d}\left(\mathcal{D}, \mathcal{D}^{\prime}, S\right)}\end{array} L(X,χ′,D,D′;Y,Y′,S)=Lp(X,Y)+Lp(X′,Y′)+λLd(D,D′,S)
可见损失函数由两项组成,其中一项为特征点检测loss L p \mathcal{L}_{p} Lp ,另外一项是描述子的loss L d \mathcal{L}_{d} Ld。
对于检测项loss,此时采用了交叉熵损失函数:
L p ( X , Y ) = 1 H c W c ∑ h = 1 w = 1 H c , W c l p ( x h w ; y h w ) \mathcal{L}_{p}(\mathcal{X}, Y)=\frac{1}{H_{c} W_{c}} \sum_{h=1 \atop w=1}^{H_{c}, W_{c}} l_{p}\left(\mathbf{x}_{h w} ; y_{h w}\right) Lp(X,Y)=HcWc1w=1h=1∑Hc,Wclp(xhw;yhw)
其中:
l p ( x h w ; y ) = − log ( exp ( x h w y ) ∑ k = 1 65 exp ( x h w k ) ) l_{p}\left(\mathbf{x}_{h w} ; y\right)=-\log \left(\frac{\exp \left(\mathbf{x}_{h w y}\right)}{\sum_{k=1}^{65} \exp \left(\mathbf{x}_{h w k}\right)}\right) lp(xhw;y)=−log(∑k=165exp(xhwk)exp(xhwy))
描述子的损失函数:
L d ( D , D ′ , S ) = 1 ( H c W c ) 2 ∑ h = 1 w = 1 H c , W c ∑ h ′ = 1 w ′ = 1 H c , W c l d ( d h w , d h ′ w ′ ′ ; s h w h ′ w ′ ) \mathcal{L}_{d}\left(\mathcal{D}, \mathcal{D}^{\prime}, S\right)=\frac{1}{\left(H_{c} W_{c}\right)^{2}} \sum_{h=1 \atop w=1}^{H_{c}, W_{c}} \sum_{h^{\prime}=1 \atop w^{\prime}=1}^{H_{c}, W_{c}} l_{d}\left(\mathbf{d}_{h w}, \mathbf{d}_{h^{\prime} w^{\prime}}^{\prime} ; s_{h w h^{\prime} w^{\prime}}\right) Ld(D,D′,S)=(HcWc)21w=1h=1∑Hc,Wcw′=1h′=1∑Hc,Wcld(dhw,dh′w′′;shwh′w′)
其中 l d l_{d} ld为Hinge-loss(合页损失函数,用于SVM,如支持向量的软间隔,可以保证最后解的稀疏性);
l d ( d , d ′ ; s ) = λ d ∗ s ∗ max ( 0 , m p − d T d ′ ) + ( 1 − s ) ∗ max ( 0 , d T d ′ − m n ) l_{d}\left(\mathbf{d}, \mathbf{d}^{\prime} ; s\right)=\lambda_{d} * s * \max \left(0, m_{p}-\mathbf{d}^{T} \mathbf{d}^{\prime}\right)+(1-s) * \max \left(0, \mathbf{d}^{T} \mathbf{d}^{\prime}-m_{n}\right) ld(d,d′;s)=λd∗s∗max(0,mp−dTd′)+(1−s)∗max(0,dTd′−mn)
同时指示函数为 s h w h ′ w ′ s_{h w h^{\prime} w^{\prime}} shwh′w′, S S S表示所有正确匹配对集合:
s h w h ′ w ′ = { 1 , if ∥ H p h w ^ − p h ′ w ′ ∥ ≤ 8 0 , otherwise s_{h w h^{\prime} w^{\prime}}=\left\{\begin{array}{ll}{1,} & {\text { if }\left\|\widehat{\mathcal{H} \mathbf{p}_{h w}}-\mathbf{p}_{h^{\prime} w^{\prime}}\right\| \leq 8} \\ {0,} & {\text { otherwise }}\end{array}\right. shwh′w′={1,0, if ∥∥∥Hphw −ph′w′∥∥∥≤8 otherwise
网络训练
本文一共设计了两个网络,一个是BaseDetector,用于检测角点(注意,此处提取的并不是最终输出的特征点,可以理解为候选的特征点),另一个是SuperPoint网络,输出特征点和描述子。
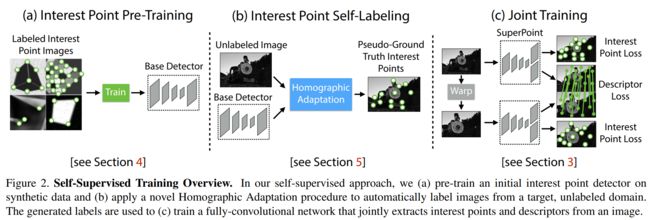
网络的训练共分为三个步骤:
- 第一步是采用虚拟的三维物体作为数据集,训练网络去提取角点,这里得到的是
BaseDetector即,MagicPoint; - 使用真实场景图片,用第一步训练出来的网络
MagicPoint+Homographic Adaptation提取角点,这一步称作兴趣点自标注(Interest Point Self-Labeling) - 对第二步使用的图片进行几何变换得到新的图片,这样就有了已知位姿关系的图片对,把这两张图片输入SuperPoint网络,提取特征点和描述子。
预训练Magic Point
此处参考作者之前发表的一篇论文Toward Geometric Deep SLAM,其实就是MagicPoint,在此不做展开介绍。
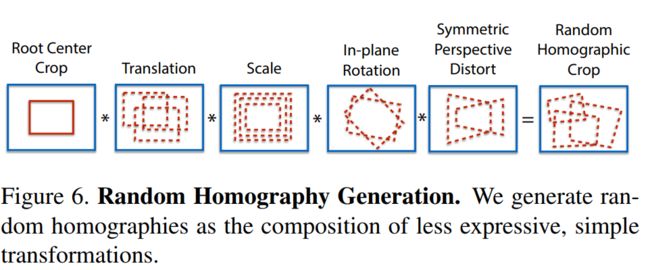
Homographic Adaptation
算法在虚拟数据集上表现极其优秀,但是在真实场景下表示没有达到预期,此时本文进行了Homographic Adaptation。
作者使用的数据集是MS-COCO,为了使网络的泛化能力更强,本文不仅使用原始了原始图片,而且对每张图片进行随机的旋转和缩放形成新的图片,新的图片也被用来进行识别。这一步其实就类似于训练里常用的数据增强。经过一系列的单映变换之后特征点的复检率以及普适性得以增强。值得注意的是,在实际训练时,这里采用了迭代使用单映变换的方式,例如使用优化后的特征点检测器重新进行单映变换进行训练,然后又可以得到更新后的检测器,如此迭代优化,这就是所谓的self-supervisd。
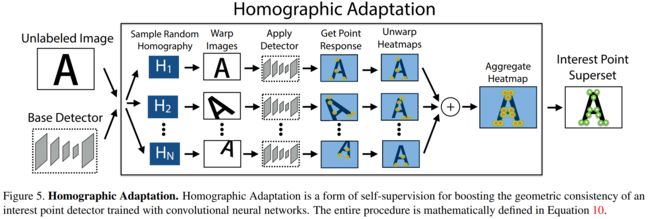
最后的关键点检测器,即 F ^ ( I ; f θ ) \hat{F}\left(I ; f_{\theta}\right) F^(I;fθ),可以表示为再所有随机单映变换/反变换的聚合:
F ^ ( I ; f θ ) = 1 N h ∑ i = 1 N h H i − 1 f θ ( H i ( I ) ) \hat{F}\left(I ; f_{\theta}\right)=\frac{1}{N_{h}} \sum_{i=1}^{N_{h}} \mathcal{H}_{i}^{-1} f_{\theta}\left(\mathcal{H}_{i}(I)\right) F^(I;fθ)=Nh1i=1∑NhHi−1fθ(Hi(I))
构建残差,迭代优化描述子以及检测器
利用上面网络得到的关键点位置以及描述子表示构建残差,利用ADAM进行优化。
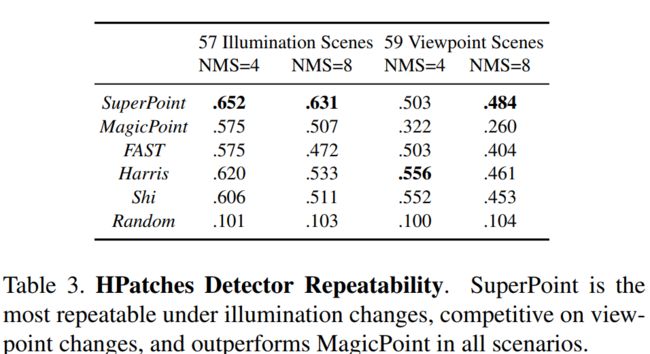
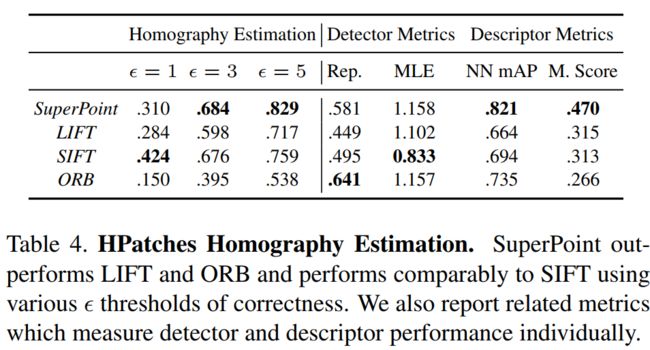
实验结果
总结
- it is possible to transfer knowledge from a synthetic dataset onto real-world images
- sparse interest point detection and description can be cast as a single, efficient convolutional neural network
- the resulting system works well for geometric computer vision matching tasks such as Homography Estimation
未来工作:
- 研究Homographic Adaptation能否在语义分割任务或者目标检测任务中有提升作用
- 兴趣点提取以及描述这两个任务是如何影响彼此的
作者最后提到,他相信该网络能够解决SLAM或者SfM领域的数据关联,并且*learning-based前端可以使得诸如机器人或者AR等应用获得更加鲁棒*。