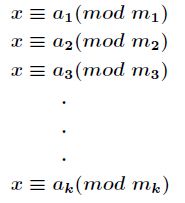数学复习（2017NOIP集训）

1.求最大公约数（辗转相除，更相减损）
2.求约数个数以及约数和（单个求和区间求）
3.拓展欧几里得算法（解同余方程，不定方程，算乘法逆元）
4.筛素数（线性筛）
5.求乘法逆元（费马小定理，拓展欧几里得定理，递推式）
6.二项式定理
7.中国剩余定理
8.容斥定理
9.欧拉函数（单个求，区间求）
10.排列组合
11.中位数
12.Catalan数

1.求最大公约数
1.辗转相除就不多说了（不会的话下面你也不用看了）
2.更相减损法（对于求解特别特别大的两个数的最大公约数）

操作过程: 对于gcd(a,b)
1.a为奇数，b为偶数，gcd(a,b)=gcd(a,b div 2)
2.a为偶数，b为奇数，gcd(a,b)=gcd(a div 2,b)
3.a和b同为偶数，gcd(a,b)=gcd(a div 2,b div 2)*2;
4.a和b同为奇数，gcd(a,b)=gcd(a-b,b)（这是在a>b的情况下，总之是大的减小的，然后把较大的数放在前面会方便操作）

其实真正步骤是第四种，但是前三种可以大大降低时间复杂度
注意：能用到更相减损肯定要用高精度的，而且大多数要丧心病狂的压位，而且还要压好多位

2.求约数个数(以及n！中有多少个质因数)

一.求n！中有多少个质因数（如果求n!的话就是把这些乘起来）
f[i]表示筛出的小于等于n的质数(m为最大个数)
for i:=1 to m do
begin
y:=n; z:=0;
while y>=f[i] do begin y:=y div f[i]; z:=z+y; end;
d[i]:=z;
end;

二.求一个数n的约数个数
只筛选这一个数的质因数以及记录个数
例：A=p1^a*p2^b*p3^c
A的约数个数为(a+1) * (b+1) * (c+1)

三.求1~n的约数个数和
way1.
ans:=0
for i:=1 to n do
ans:=ans+(n div i);

way2.(思路：对于某一些约数个数相同的约数放在一起处理)
举个例子：求取小于等于12的数的约数个数
约数：12 11 10 9 8 7 6 5 4 3 2 1
个数: 1 1 1 1 1 1 2 2 3 4 6 12
发现总是有一段区间的约数个数是一样的，所以想办法把个数相同的放在一起

l,r表示约数个数相同的一段区间，(n div l)就是相同的这个约数个数为多少，
(r-l+1)就是区间长度，所以总约数个数就是(n div l)*(r-l+1)
ans:=0;
l:=1;
while l<=n do
begin
r:=n div (n div l);
ans:=ans+(n div l)*(r-l+1);
l:=r+1;
end;
exit(ans);

四：求1~n的所有约数的和
对于上面这种情况，少许变更即可
对于一段约数个数相同的区间，约数分别为l…..r,总个数为(r-l+1) *（n div l）
采用平均数的思想，即这段区间的约数和为(r-l+1) * (n div l) * (l+r) div 2(这是一定能整除的)
ans:=0;
l:=1;
while l<=n do
begin
r:=n div (n div l);
ans:=ans+(n div l) * (r-l+1) * （l+r） div 2;
l:=r+1;
end;
exit(ans);

五：求单个数的约数和
A=p1^a * p2^b * p3^c
约数和ans:=(1+p1+…+p1^a) * (1+p2+….+p2^b) * (1+p3+……+p3^c)

3.拓展欧几里得算法
应用：对于ax+by=gcd(a,b)，求解x和y

1.求解同余方程：ax≡c(mod b)
例题：青蛙的约会（裸题）

2.求解乘法逆元
例：求a在mod p下的逆元
相当于解ax≡1(mod p)
求解x即可

4.线性筛素数
没什么好讲的
一种加的，一种乘的

乘法

t:=0;
for i:=2 to n do
begin
if not b[i] then
begin
inc(t);
f[t]:=i;
end;
for j:=1 to t do
if i*f[j]<=n then
begin
b[i*f[j]]:=true;
if i mod f[j]=0 then break;
end else break;
end;

加法

t:=0;
for i:=2 to n do
begin
if not b[i] then
begin
inc(t);
f[t]:=i;
end;
j:=i;
while j+i<=n do
begin
j:=j+i;
b[j]:=true;
end;
end;

5.求乘法逆元
（a在mod p下的乘法逆元）
1.费马小定理
—————————————————-不懂的自己查查
这种方法有较大的限制条件
要求a与p必须互质，求解十分简单直接求解a^(p-2)即可

2.拓展欧几里得定理
相当于解ax≡1(mod p)，ax+py=1
求解x就好（似乎说过一遍了）

3.一个很好用的递推式，上面两种方法都大多只适合求单个或较少的，这种适合于n不是太大，但是较多的时候
用f[i]记录i的乘法逆元
f[i]:=(p-(p div i))*f[p mod i] mod p;
公式推导：
令k:=p div i,t=p mod i
则一定有k*i+t=p;
即 k*i+t≡0(mod p)
-k*i≡t(mod p)
两边同时除以t*i，得到
-k*(1/t)≡(1/i) (mod p)
即 -k*f[t]≡f[i] mod p
展开得到 f[i]:=(p-k)*f[t] mod p； （这个多的p*f[t]想想怎么来的）
即f[i]:=(p-(p div i))*f[p mod i] mod p;

6.二项式定理

去翻高中课本吧

7.中国剩余定理
对于一组同余方程（未完待续）

正整数m1,m2,m3,……,mk两两互素，则同余方程组

有整数解。并且在模下的解是唯一的，解为

其中，，而为Mi模mi的逆元。

例题1：POJ1006生物节律

题意：人自出生起就有体力，情感和智力三个生理周期，分别为23，28和33天。一个周期内有一天为峰值，在这一天，人在对应的方面（体力，情感或智力）表现最好。通常这三个周期的峰值不会是同一天。现在给出三个日期，分别对应于体力，情感，智力出现峰值的日期。然后再给出一个起始日期，要求从这一天开始，算出最少再过多少天后三个峰值同时出现。

例题2：vijos曹冲养猪
自从曹冲搞定了大象以后，曹操就开始捉摸让儿子干些事业，于是派他到中原养猪场养猪，可是曹冲满不高兴，于是在工作中马马虎虎，有一次曹操想知道母猪的数量，于是曹冲想狠狠耍曹操一把。举个例子，假如有16头母猪，如果建了3个猪圈，剩下1头猪就没有地方安家了。如果建造了5个猪圈，但是仍然有1头猪没有地方去，然后如果建造了7个猪圈，还有2头没有地方去。你作为曹总的私人秘书理所当然要将准确的猪数报给曹总，你该怎么办？
格式

输入格式

第一行包含一个整数n (n <= 10) – 建立猪圈的次数，解下来n行，每行两个整数ai, bi( bi <= ai <= 1000), 表示建立了ai个猪圈，有bi头猪没有去处。
//你可以假定ai,aj互质.
输出格式

输出包含一个正整数，即为曹冲至少养母猪的数目。

解法1：拓展欧几里得求乘法逆元（这种方法极度不喜欢）

解法2：直接逐级满足（个人认为操作简单，而且要更快一些）

对于最终结果
x≡b1(mod a1)
x≡b2(mod a2)
.
.
.
x≡bi( mod ai)

采用逐级满足，求取lcm(b1,b2,…,b(i-1)),当前x不满足就+lcm，直到满足为止

program df;
var i,j,n,z,k,t:longint;
a,b,c,d:int64;

function gcd(a,b:int64):int64;
begin
if b=0 then exit(a)
else exit(gcd(b,a mod b));
end;

begin
readln(n);
readln(a,b);
for i:=2 to n do
begin
readln(c,d);
while b mod c<>d do b:=b+a;
a:=(a*c) div gcd(a,c);
end;
writeln(b);
end.

8.容斥定理
定义极其简单，就是先求总和，然后减去不满足的情况，或者多余的情况
主要问题在于怎么理解题目，这类题大部分题目都是情况一旦分类出来，就做出来了

9.欧拉函数
对于φ（n）的定义是小于n且与n互质的数的个数

1.对于单个的欧拉函数
A=p1^a1 * p2^b * p3^c
则φ（n）=n * (1-1/p1) * (1-1/p2) * (1-1/p3);

2.对于1~n的欧拉函数的求解
线性筛素数中处理即可（phi[i]即为所求）
t:=0;
for i:=2 to n do
begin
if not b[i] then
begin
inc(t);
f[t]:=i;
phi[i]:=i-1;
end;
for j:=1 to t do
if i*f[j]<=n then
begin
b[i*f[j]]:=true;
if i mod f[j]=0 then begin phi[i*f[j]]:=phi[i]*f[j]; break; end;
phi[i*f[j]]:=phi[i]*(f[j]-1);
end
else break;
end;

10.排列组合
一些基本的就不讲了，讲一些不是特别常见的

1.快速求c(n,m)
其实就是上面的求解y！中的各个质因子的个数
c(n,m)=n!/(m!*(n-m)!)
求解n！中的质因子，再求解m！和(n-m)!中质因子的个数，最后乘起来就好

代码再放一遍：(f[i]为筛出的质数，t为到恰好<=n的质数的个数)

procedure check(y,x:longint):longint;
var ans:longint;
begin
ans:=0;
while y>=x do begin y:=y div x; ans:=ans+y; end;
exit(ans);
end;

for j:=1 to t do
c(n,m)=check(n,f[i])-check(m,f[i])-check(n-m,f[i]);

（未完待续………)

11.中位数（带权中位数）
中位数和带权中位数其实是一样的
对于一个题目，给你一些坐标，给你点和距离的关系，让你寻找一个最合适的放置位置使得值最小（多半是贪心的思想，有一些要推公式）

对于没有权值的中位数，权值默认为1就好了（直接取中间的数），有权值的则求和处理

例题：codeVS 3625 士兵战队
http://codevs.cn/problem/3625/

因为要站成一排

对于x坐标先排序一遍，对于要选择的中间点要满足
|xk-(k-1)-x1|+|xk-(k-2)-x2 |+ ……..|xk-(k-n)-xn | 是最小的
分离变量得到abs(xk-k)*n+1-x1+2-x2+…..+n-xn 所以，对于xi-i再排序一边即可

program df;
var i,j,n,m,x,y,z,k,t,ans:longint;
a,b,c:array[0..200000] of longint;
procedure sq(l,r:longint);
var i,j,mm,dd:longint;
begin
i:=l; j:=r;
mm:=a[(l+r) div 2];
repeat
while a[i]do inc(i);
while a[j]>mm do dec(j);
if i<=j then
begin
dd:=a[i]; a[i]:=a[j]; a[j]:=dd;
dd:=b[i]; b[i]:=b[j]; b[j]:=dd;
inc(i); dec(j);
end;
until i>j;
if lthen sq(l,j);
if ithen sq(i,r);
end;

procedure sq2(l,r:longint);
var i,j,mm,dd:longint;
begin
i:=l; j:=r;
mm:=b[(l+r) div 2];
repeat
while b[i]do inc(i);
while b[j]>mm do dec(j);
if i<=j then
begin
dd:=a[i]; a[i]:=a[j]; a[j]:=dd;
dd:=b[i]; b[i]:=b[j]; b[j]:=dd;
inc(i); dec(j);
end;
until i>j;
if lthen sq2(l,j);
if ithen sq2(i,r);
end;


begin
readln(n);
ans:=0;
for i:=1 to n do
readln(a[i],b[i]);

sq(1,n);
for i:=1 to n do
a[i]:=a[i]-i;

sq(1,n);
x:=a[n div 2+1];

for i:=1 to n do
ans:=ans+abs(x-a[i]);

sq2(1,n);
x:=b[n div 2+1];

for i:=1 to n do
ans:=ans+abs(x-b[i]);
writeln(ans);
end.

例题2. codeVS 2616安装服务器
http://codevs.cn/problem/2616/

最简单的带权中位数，直接排序取中间值即可

program df;
var i,j,n,m,x,y,z,k,t:longint;
a,b,c:array[0..200000] of longint;
procedure sq(l,r:longint);
var i,j,mm,dd:longint;
begin
i:=l; j:=r;
mm:=a[(l+r) div 2];
repeat
while a[i]

program df;
var i,j,n,m,x,y,z,k,t:longint;
ans:int64;
a,b,c,d,e,f:array[0..100000] of longint;
procedure sq(l,r:longint);
var i,j,mm,dd:longint;
begin
i:=l; j:=r;
mm:=e[(l+r) div 2];
repeat
while e[i]do inc(i);
while e[j]>mm do dec(j);
if i<=j then
begin
dd:=e[i]; e[i]:=e[j]; e[j]:=dd;
inc(i); dec(j);
end;
until i>j;
if lthen sq(l,j);
if ithen sq(i,r);
end;



begin
assign(input,'tanabata.in');
reset(input);
assign(output,'tanabata.out');
rewrite(output);
readln(n,m,t);
for i:=1 to t do
begin
readln(x,y);
inc(a[x]); inc(b[y]);
end;
if (t mod n=0) and (t mod m=0) then write('both ')
else if t mod n=0 then write('row ')
else if t mod m=0 then write('column ')
else
begin
writeln('impossible');
close(input);
close(output);
halt;
end;



if t mod n=0 then
begin
k:=t div n;
for i:=1 to n-1 do
c[i]:=c[i-1]+a[i]-k;
e:=c;
sq(0,n-1);
c:=e;
for i:=0 to n-1 do
ans:=ans+abs(c[n div 2]-c[i]);
end;
if t mod m=0 then
begin
k:=t div m;
for i:=1 to m-1 do
d[i]:=d[i-1]+b[i]-k;
e:=d;
sq(0,m-1);
d:=e;

for i:=0 to m-1 do
ans:=ans+abs(d[m div 2]-d[i]);
end;
writeln(ans);
close(input);
close(output);
end.

---

---

12.catalan数
令h(0)=1,h(1)=1，catalan数满足递推式[1] ：
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + … + h(n-1)h(0) (n>=2)
例如：h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
另类递推式[2] ：
h(n)=h(n-1)*(4*n-2)/(n+1);
递推关系的解为：
h(n)=C(2n,n)/(n+1) (n=0,1,2,…)
递推关系的另类解为：
h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,…)

---

P1363 火车进出栈问题
时间: 1000ms / 空间: 131072KiB / Java类名: Main
描述

一列火车n节车厢，依次编号为1,2,3,…,n。每节车厢有两种运动方式，进栈与出栈，问n节车厢出栈的可能排列方式有多少种。
输入格式

一个数，n(n<=30000)
输出格式

一个数s表示n节车厢出栈的可能排列方式
测试样例1

输入

3
输出

5

---

思路：首先知道catalan数通项公式：h(n)=c（2n,n）/(n+1);
说白了就是求c（2n,n）（这个公式再不知道我也是没辙），
将每个数分解质因数，n+1 to 2*n 的每个质因数个数加上（因为要除（n+1），所以从n+2开始），1 to n-m的每个质因数个数减去，数组记录，最后高精乘以单精，轻松AC Σ(っ °Д °;)っ

---

program df; 
 var i,j,n,m,x,y,z,k,t:longint; 
 a,d:array[0..100000] of longint; 
 procedure deal(n,m:longint); 
 var i,j,x,y:longint; 
 begin 
 for i:=m+2 to n do 
 begin 
 x:=i; 
 for j:=2 to trunc(sqrt(x)) do 
 while x mod j=0 do 
 begin 
 inc(d[j]); 
 x:=x div j; 
 end; 
 if x>1 then inc(d[x]); 
 end; 
 for i:=1 to n-m do 
 begin 
 x:=i; 
 for j:=2 to trunc(sqrt(x)) do 
 while x mod j=0 do 
 begin 
 dec(d[j]); 
 x:=x div j; 
 end; 
 if x>1 then dec(d[x]); 
 end; 
 end;

begin 
 readln(n); 
 deal(2*n,n); 
 a[1]:=1; t:=1; 
 for i:=2 to 3*n do 
 while d[i]>0 do 
 begin 
 for j:=1 to t do 
 a[j]:=a[j]*i; 
 for x:=1 to t do 
 begin 
 a[x+1]:=a[x+1]+a[x] div 10; 
 a[x]:=a[x] mod 10; 
 end; 
 j:=t+1; 
 while a[j]<>0 do 
 begin 
 a[j+1]:=a[j+1]+a[j] div 10; 
 a[j]:=a[j] mod 10; 
 inc(j); 
 end; 
 t:=j-1; 
 dec(d[i]); 
 end; 
 for i:=t downto 1 do 
 write(a[i]); 
 end.

①、被3整除：位数和能被3整除即可；

②、被4整除：末尾两位能被4整除即可；

③、被7整除：将个位数字截去，在余下的数中减去个位数字的二倍，差是7的倍数即可；（可以递归）

④、被8整除：末尾三位能被8整除即可；

⑤、被9整除：位数和能被9整除即可；

⑥、被11整除：第一种方法就是用上面说的，还有一种是采用和“被7整除”一样的方法，不过要减去的是个位的一倍；

⑦、被12整除：同时被3和4整除；

⑧、被13整除：同“被7整除”，不过我们不是要减去，而是要加上个位的四倍；

⑨、被17整除：同“被7整除”，不过要减去的是个位数的五倍；

⑩、被19整除：同“被7整除”，不过要加上个位数的两倍；