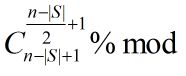2017百度之星资格赛：1005. 寻找母串（卡特兰数+分块打表）

寻找母串

 

 Accepts: 105

 

 Submissions: 887

 Time Limit: 2000/1000 MS (Java/Others)

 

 Memory Limit: 32768/32768 K (Java/Others)

Problem Description

对于一个串S，当它同时满足如下条件时，它就是一个01偏串： 1、只由0和1两种符组成； 2、在S的每一个前缀中，0的个数不超过1的个数； 3、S中0的个数和1的个数相等。

现在给定01偏串S，请计算一下S在所有长度为n的01偏串中作为子串出现的次数的总和。 由于结果比较大，结果对1e9+7取余后输出。

样例解释： 在第二个样例中，长度为4的偏串共两个1010，1100。10在1010中出现了两次，在1100中出现了1次。所以答案是3。

Input

第一行给出一个整数T(1<=T<=40),表示测试数据的数目。 每一组测试包含一个整数n和字符串S，中间用空格分开。(1<=|S|<=100000，1<=n<=1000000000)

输入保证S是一个01偏串。

Output

对于每一组数据，输出一个整数占一行，表示答案。

Sample Input

Copy

2
2 10
4 10

Sample Output

1
3

可能我姿势不对。。这表怎么就打了1年

这题看起来束手无策，但其实你可以先写个暴力观察小数据，这个时候你就会发现其实这题比你想象的要简单的多

（比如你会发现其实答案之和字符串的长度|S|有关，和字符串的内容是无关的）

没错！这题有规律，答案就是

但是别高兴的太早，这个时候你又会发现其实这题比你想象的要难得多

因为这题的n范围巨大（约10亿）而求10亿的组合数是做不到的

所有先考虑化简公式看看，令x = (n-|S|)/2+1有

其中F[x]是第x项卡特兰数

而卡特兰数有O(n)的递推公式

这样的话理论上可以O(n)求出所有的答案，可还是不行。。。

复杂度已经不能再优化了。。所以只能考虑打表

可是你又开不了10亿的数组，但是这题也没有说要O(1)询问呀

没错！分块打表

你只需要后台O(n)暴力出第100000个卡特兰数，第200000个卡特兰数……第500000000个卡特兰数就好了

也就是开个5000+的数组c[]，其中c[i]是第100000*i个卡特兰数

然后对于每组询问(n, |S|)，先计算x=(n-|S|)/2+1，然后再找到x所在的那一块（比x小离x最近的100000的倍数），

之后暴力转移就好，最多转移100000次

因为有除法所以要乘法逆元，总体复杂度O(100000log(n))

还有注意n为奇数的时候答案一定为0，因为母串要保证0和1的数量相等，所以不存在长度为奇数的母串

除此之外，n<|S|答案也为0

下面附上暴力程序+打表程序

#include
#include
char str[100005], jud[100005];
int Jud(int n)
{
	int i, s1, s0;
	s1 = s0 = 0;
	for(i=1;i<=n;i++)
	{
		if(jud[i]=='1')  s1++;
		else  s0++;
		if(s0>s1)
			return 0;
	}
	if(s1!=s0)
		return 0;
	return 1;
}
int main(void)
{
	int T, n, m, i, j, k, sum, ans;
	scanf("%d", &T);
	while(T--)
	{
		sum = ans = 0;
		scanf("%d%d", &n, &m);
		for(i=1;i<=m/2;i++)
			str[i] = '1';
		for(i;i<=m;i++)
			str[i] = '0';
		str[m+1] = 0;
		m = strlen(str+1);
		for(i=0;i<=(1<n)
							break;
					}
					if(k==m+1)
						ans++;
				}
			}
		}
		printf("%d\n", ans);
	}
	return 0;
}
/*
#include
#define mod 1000000007
#define LL long long
LL Pow(LL a, LL b)
{
	LL sum = 1;
	while(b)
	{
		if(b%2)
			sum = sum*a%mod;
		a = a*a%mod;
		b /= 2;
	}
	return sum;
}
int main(void)
{
	LL i, now = 1;
	freopen("ct.txt", "w", stdout);
	printf("{1");
	for(i=1;i<=500000000;i++)
	{
		now = 2*(2*i-1)*now%mod*Pow(i+1, mod-2)%mod;
		if(i%100000==0)
			printf(",%lld", now);
	}
	printf("};");
	return 0;
}
*/