SLAM笔记(五)光束平差法(Bundle Adjustment)
###1.什么是光束平差法
前边的八点法,五点法等可以求出闭式解的前提是已经知道确切的点对。但实际情况中往往存在大量的噪声,点与点不是精确地对应甚至出现一些错误匹配。
光束平差法由Bundle Adjustment翻译得来,有两层意思:
对场景中任意三维点P,由从每个视图所对应的的摄像机的光心发射出来并经过图像中P对应的像素后的光线,都将交于P这一点,对于所有三维点,则形成相当多的光束(bundle);实际过程中由于噪声等存在,每条光线几乎不可能汇聚与一点,因此在求解过程中,需要不断对待求信息进行调整(adjustment),来使得最终光线能交于点P。对m帧,每帧含N个特征点的目标函数如下:
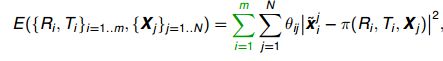
(1)
其中: x ~ \widetilde x x 表示受白噪声影响的估计二维点坐标, π \pi π为投影函数,ruguo 如果点j出现在图i上,则 θ = 1 \theta = 1 θ=1,否则 θ i j = 0 \theta_{ij} = 0 θij=0。
这是一个非凸问题。
式子(1)表示对所有点
以上便是光束平差法目标函数的原理。由于场景中特征点往往较多,该问题是一个巨大的高维非线性优化问题。接下来,需要对上述式子进行求解,这是光束平差法的核心内容。
针对具体应用场景,光束平差法有不同收敛方法。目前常用的方法有梯度下降法,牛顿法,高斯牛顿法,Levenber-Marquardt等方法。
2.1 一阶方法——梯度下降法
所谓一阶方法,即对问题的目标函数进行泰勒一阶展开后进行迭代求解的方法。梯度下降法是一阶方法之一。当梯度为负值时,沿着梯度方向就是函数值f变小最快的方向。梯度下降法就是让函数沿着下降最快的方向去找函数值的最小值,就像水流沿着斜率最大的方向流去。对于变量都为标量的函数,形象的描述是始终用一条直线来拟合曲线。梯度下降法迭代式子如下:
x k + 1 = x k − ϵ d E ( x k ) / d x x_{k+1}=x_k−ϵdE(x_k)/d_x xk+1=xk−ϵdE(xk)/dx(2)
其中,ϵ表示自己设置的迭代步长,可用一维线性搜索动态确定。x表示自变量。
严格意义上,梯度下降法并不决定函数f(x)下降方向,因为它仅仅是一个余向量而非向量,只能通过最终标量的正负而非实际的向量指引函数下降方向。梯度下降法的复杂度是Ο(n),其中n为待解决问题的大小,比如矩阵E的行数。实际过程中,常常使用一维线性搜索方法来寻找合适的步长。
2.2 二阶方法——牛顿法(Newton Method)
牛顿法是二阶优化方法,即会将目标函数展开至泰勒二阶项然后进行优化求解。与梯度法相比,它们利用到了目标函数的二阶导数。形象地讲,如用牛顿法求解自变量为标量的函数时,用二次曲线来拟合最优化点时的函数曲线。
对目标函数E,其二阶泰特展开式为:
E ( x ) ≈ E ( x t ) + g T ( x − x t ) + 1 / 2 ∗ ( x − x t ) T H ( x − x t ) E(x)≈E(x_t)+g^T(x−x_t)+1/2*(x−xt)^TH(x−x_t) E(x)≈E(xt)+gT(x−xt)+1/2∗(x−xt)TH(x−xt)
(3)
其中g为E的雅克比矩阵,H为E的海塞矩阵。
由于优化点的导数为0,即:
d E / d x = g + H ( x − x t ) = 0 dE/d_x=g+H(x−x_{t})=0 dE/dx=g+H(x−xt)=0
(4)
上式展开,易知x的迭代式子为:
x k + 1 = x k − H − 1 g x_{k+1}=x_k-H^{−1}g xk+1=xk−H−1g (5)
由于牛顿法下降速度很快。实际中往往加上一个步长因子γϵ(0,1),来控制收敛的速度:
x k + 1 = x k − γ H − 1 g x_{k+1}=x_k-\gamma H^{−1}g xk+1=xk−γH−1g
(6)
牛顿法是二阶收敛的,收敛速度很快。在实际应用中,向量x往往非常大(每个视图中图像处理后特征点数量可能达到万个以上),海森矩阵H将非常大,求海塞矩阵的逆的运算消耗将非常大,对于牛顿法来说,计算复杂度是O(n3)。此外,由于海塞矩阵不一定可逆。其三,对于大多数一阶优化方法,可以采用诸如图形处理器(Graphics Processing Unit)并行的方式来加速,但对于海塞矩阵求逆来说这显然无法实现。因此实际中往往出现一阶方法比二阶方法更快收敛。
2.3 拟牛顿法——高斯牛顿法(Gauss-Newton Method)
所谓拟牛顿法,就是用其他式子来模拟替代海塞矩阵。假如牛顿法中的海塞矩阵不是正定(positive definitive)的,无法求解;此外,海森矩阵H往往非常大,求海塞矩阵的逆的运算消耗也很大(对于牛顿法来说,计算复杂度是O(n3)),因此,引入用拟牛顿法来用正定矩阵代替海塞矩阵和海塞矩阵的逆。常用的拟牛顿法有高斯牛顿法(Gauss-Newton Method)。
假设最小二乘问题目标函数如下:
min x ∑ i r i ( x ) 2 \min _x \sum_i r_i(x)^2 xmini∑ri(x)2
(7)
其中ri(x)是对应观测值与预测值之间的残差。
仿照2.3可以得到牛顿法中的迭代式子(10)。不过其中梯度矩阵g:
g j = 2 ∑ i r i ∂ r i ∂ x j g_j=2\sum_i r_i \frac {\partial r_i}{\partial x_j} gj=2i∑ri∂xj∂ri
, (8)
海塞矩阵H:
H j k = 2 ∑ i ( ∂ r i ∂ x j ∂ r i ∂ x k + r i ∂ 2 r i ∂ x j ∂ x k ) H_{jk}=2\sum_i(\frac {∂r_i}{∂x_j}\frac {∂r_i}{∂x_k}+ri\frac{∂^2r_i}{∂x_j∂x_k}) Hjk=2i∑(∂xj∂ri∂xk∂ri+ri∂xj∂xk∂2ri)
(9)
如果对于一个近线性的优化问题,则上式第二项更趋近于0,因此舍弃第二项,上式为:
H j k = 2 ∑ i ∂ r i ∂ x j ∂ r i ∂ x k H_{jk}=2\sum_i\frac {∂r_i}{∂x_j}\frac {∂r_i}{∂x_k} Hjk=2i∑∂xj∂ri∂xk∂ri
(10)
则: g = J T r , H ≈ 2 J T J , J = d r d x g=J^Tr,H≈2J^TJ,J=drdx g=JTr,H≈2JTJ,J=drdx
也即有:
x t + 1 = x t + ∆ , w i t h ∆ = − ( J T J ) − 1 ( J T r ) x_{t+1}=x_t+∆,with∆=−(J^TJ)^{−1}(J^Tr) xt+1=xt+∆,with∆=−(JTJ)−1(JTr)(11)
由于采用 ( J T J ) − 1 ( J T J ) (J^TJ)^{−1}(J^TJ) (JTJ)−1(JTJ) ,计算量大大减少
应当特别指出,上式成立的条件是 ∣ ∣ ∂ r i ∂ x j ∂ r i ∂ x k ∣ ∣ > > ∣ ∣ r i ∂ 2 r i ∂ x j ∂ x k ∣ ∣ ||\frac {∂r_i}{∂x_j}\frac {∂r_i}{∂x_k}||>>||ri\frac{∂^2r_i}{∂x_j∂x_k}|| ∣∣∂xj∂ri∂xk∂ri∣∣>>∣∣ri∂xj∂xk∂2ri∣∣。在结构与运动过程中,由于一般认为到场景位置点的距离比较远的,因此短暂的移动过程中,可以认为从摄像机到场景位置点的距离是近似不变的。在距离不变,也就是一个维度固定的前提下,投影函数π是线性的。因此该近似符合应用场景,是很好的近似。
2.4 Levenberg-Marquardt方法
另外一种思路是将牛顿法和梯度法融合在一起。数学上是阻尼最小二乘法的思路,即近似只有在区间内才可靠。对于
min x ∑ i r i ( x ) 2 , s . t . ‖ D ∆ ‖ 2 ≤ μ \min_x\sum_i ri(x)^2 ,s.t.‖D∆‖2≤μ xmini∑ri(x)2,s.t.‖D∆‖2≤μ (12)
此处μ是信赖区间半径,D为对∆进行转换的矩阵(在Levenberg的方法中,他将D设置为单位矩阵)。
即加上一个单位矩阵I的倍数和使之成为:
x k + 1 = x k − ( H + λ I ) − 1 g x_{k+1}=x_k−(H+λI)^{−1}g xk+1=xk−(H+λI)−1g
(13)
这种方法时保证改进后的海塞矩阵可逆且正定。从效果上,是用λ在牛顿法与梯度法之间做出权衡。当λ很小时,上式几乎等同与牛顿法式子,当λ很大时,上式等同于梯度下降法的式子。
后来,Levenberg(1944)对此方法进行了改进。他将H替换成高斯牛顿法中的拟合矩阵:
x t + 1 = x t − ∆ x_{t+1}=x_t-∆ xt+1=xt−∆
(14)
其中: ∆ = ( J T J + λ I ) − 1 ( J T J ) r ∆=(J^TJ+λI)^{−1}(J^TJ)r ∆=(JTJ+λI)−1(JTJ)r (15)
但容易出现的问题是,当 J T J J^TJ JTJ 很小的时候,λI可能很大。这样会极大地偏向梯度法,降低收敛速度。因此为了提高收敛速度,Marquardt 提出了一种新的自适应方法:它的迭代式子中:
∆ = − ( J T J + λ d i a g ( J T J ) ) − 1 ( J T J ) r ∆=−(J^TJ+λdiag(J^TJ))^{−1}(J^TJ)r ∆=−(JTJ+λdiag(JTJ))−1(JTJ)r
(16)
因此当 J T J J^TJ JTJ很小时,该方法也不会特别偏向梯度法。
在L-M方法中,采用了近似程度描述ρ
ρ = f ( x + d x ) − f ( x ) J d x ρ=\frac {f(x+dx)−f(x)}{Jdx} ρ=Jdxf(x+dx)−f(x)
(17)
即ρ=实际下降/近似下降。当ρ太大,则减少近似范围(增大λ),当p太大,则增加近似范围(减少λ)。
因此最常使用的光束平差法模型, L-M算法计算步骤如下:
a)给定初始值;
b)对第k次迭代,求解
c)计算ρ
d)若ρ>0.75(经验值),则μ=2μ(经验值,实际可视作变化迭代步长);
若ρ<0.25(经验值),则μ=0.5μ(经验值);
e)如果ρ大于某阈值,则该次近似是可行的,回到b)继续迭代;否则算法已经收敛,迭代结束。
2.5与高斯牛顿法相比LM算法的优缺点
高斯牛顿法的缺点是:
- J t J J^tJ JtJ可能是奇异的病态的,无法保证求解的增量的稳定性;
- 步长可能很大从而导致无法满足高斯牛顿的一阶能大致拟合的假设
优点: - 下降速度比LM快
LM是信赖区域优化法的代表,而加上步长的高斯牛顿法是线搜索方法的代表。
3 关于光束平差法的其他问题
(1)初始值
光束平差法需要比较好的初始值才能比较快地收敛,所以光束平差法一般作为重建流水线的最后一个步骤,在此之前,需要使用多视图几何中传统的八点法,五点法等传统多视图几何算法先算出R,T等信息。
(2)步长控制
引入步长控制,既可以是避免收敛时步长太大而在最优点附近震荡,也可以加快收敛速度。加入迭代步长的原因,是因为 牛顿法中 下降方向 可能和真实下降方向不一致** 。**比如可能会出现几个最优点相邻比较近的情况,那么优化过程将在几个谷底之间跳来跳去迟迟不收敛。为了避免这种情况,增加收敛速率,加入一个迭代步长γ,来使迭代朝着真实下降方向走。如果在鞍点,在沿着海塞矩阵为负的方向迭代。实际应用中,可以采用每一次迭代后,再对γ进行一维搜索的方法来寻找合适步长。也可以采用L-M的方法,通过改变信任区间的方式,来进行步长控制。
4.常用优化库:
常用BA库:
sba: A Generic Sparse Bundle Adjustment C/C++
Apero/MicMac, a free open source photogrammetric software. Cecill-B licence.
Package Based on the Levenberg–Marquardt Algorithm (C, MATLAB). GPL.
cvsba: An OpenCV wrapper for sba library (C++). GPL.
ssba: Simple Sparse Bundle Adjustment package based on the Levenberg–Marquardt Algorithm (C++). LGPL.
OpenCV: Computer Vision library in the contrib module. BSD license.
mcba: Multi-Core Bundle Adjustment (CPU/GPU). GPL3.
libdogleg: General-purpose sparse non-linear least squares solver,based on Powell’s dogleg method. LGPL.
ceres-solver: A Nonlinear Least Squares Minimizer. BSD license.
g2o: General Graph Optimization (C++) - framework with solvers for sparse graph-based non-linear error functions. LGPL.
DGAP: The program DGAP implement the photogrammetric method of bundle adjustment invented by Helmut Schmid and Duane Brown. GPL.
工程上常用的是g2o和ceres-solver。此上列表来源不可考,如有侵权请联系我以删除。