hdu1253 胜利大逃亡--BFS & BFS的总结

原题链接： http://acm.hdu.edu.cn/showproblem.php?pid=1253

一：题意

一个三维A*B*C，起点（0,0,0），终点（A-1,B-1,C-1），求在 t 时间内（包括t）能否到达？可以，输出花费的最少时间，否则输出-1。

二：分析

BFS，以前用的BFS都是用优先队列，优先取出step的最小值，每走一步要判断即将要新走的这一步的位置的step值和上一个的step+1的大小，只有更小这样才能走，这样找到目标后肯定就是最小值，但是看了别人的代码，借助queue，然后都是用一个vis数组标记该点是否走过，当时就想，这样不是不严谨么，下面是我当时我想的一个例子来推翻vis数组标记法：

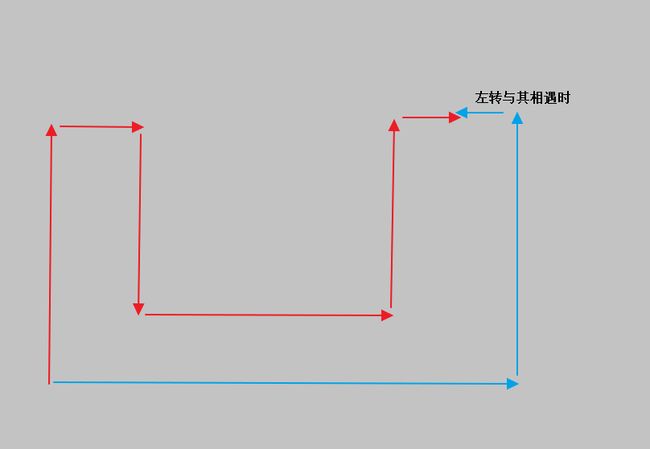
假如红线先到末尾箭头处，不妨设为A点，此时A的位置vis被标记成1，step假如为n+2。

现在蓝线左转正好遇见A点，但是由于A点被标记，不得不放弃走这一条路，但是如果蓝线的这条路就是题目所求呢，既然是题目所求，那么蓝线的step肯定是比较小的，我们假设蓝线在没走A点时的step是n，那么现在走了一步A点，就是n+1，明显比红线的n+2小，这样就推翻了使用vis标记数组来做事不对的，至少是不严谨的，我当时认为的正确的做法就是：每走一步要判断即将要新走的这一步的位置的step值和上一个的step+1的大小，只有更小这样才能走。

到了第二天，我想想可能是我想错了，重新想了下，果然是我错了，上述的情况是不可能发生的，也就是n与n+2的同时存在，这是不可能的。我们知道bfs搜索相似一个晕，就像你在湖上扔一个石子，必定出现一条条波纹，由里往外，这个过程和bfs相似，那么我说下为什么n与n+2的情况不可能出现呢？

我们定义一个queue，step值入队列，假设搜索的空间（你可以想成就是一个二维数组）是理想的，无限大，没有障碍物。那入队的状态变化肯定是这样的，一行代表一个变化，括号内是注释：

0

1111（取0进四个方向的step值）

111222（取一个1，进3个2，读者可以纸上模拟）

1122222（再取一个1，这次只能进2个2，这个不一定，具体看你的dir方向数组是否是杂乱的）

好了，大概就这样，我想说明的是，如果当前取的step值是n，那么队列里step最大值就是n+1，不可能是n+2。

三：AC代码

#define _CRT_SECURE_NO_DEPRECATE 
#define _CRT_SECURE_CPP_OVERLOAD_STANDARD_NAMES 1 

#include 
#include 
#include 
using namespace std;
const int N = 55;

int map[N][N][N];
int vis[N][N][N];
int tx[] = { 1,-1,0,0,0,0 };
int ty[] = { 0,0,1,-1,0,0 };
int tz[] = { 0,0,0,0,1,-1 };
int a, b, c, t, ans;

struct Node
{
	int x, y, z, step;
};

int abs(int x)//绝对值
{
	return x < 0 ? -x : x;
}

int check(int i, int j, int k)//判断是否可行
{
	if (i < 0 || j < 0 || k < 0 || i >= a || j >= b || k >= c || map[i][j][k])
		return 0;
	return 1;
}

int bfs(int x, int y, int z)
{
	int i;
	queue Q;
	Node p, q;
	p.x = x;
	p.y = y;
	p.z = z;
	p.step = 0;
	vis[x][y][z] = 1;
	Q.push(p);
	while (!Q.empty())
	{
		p = Q.front();
		Q.pop();
		if (p.x == a - 1 && p.y == b - 1 && p.z == c - 1 && p.step <= t)
			return p.step;
		for (i = 0; i < 6; i++)
		{
			q = p;
			q.x += tx[i];
			q.y += ty[i];
			q.z += tz[i];
			if (!vis[q.x][q.y][q.z] && check(q.x, q.y, q.z))
			{
				q.step++;
				vis[q.x][q.y][q.z] = 1;
				//由于行走只能朝6个固定方向，这里是对剩下时间里能否走到出口进行预判，如果走最短路径依然不能再规定时间内到达出口，明显是不行的,当然不加这个判断也能AC，只是比较消耗时间
				if (abs(q.x - a + 1) + abs(q.y - b + 1) + abs(q.z - c + 1) + q.step > t)
					continue;
				Q.push(q);
			}
		}
	}
	return -1;
}

int main()
{
	int cas;
	scanf("%d", &cas);
	while (cas--)
	{
		int i, j, k;
		scanf("%d%d%d%d", &a, &b, &c, &t);
		memset(map, 0, sizeof(map));
		memset(vis, 0, sizeof(vis));
		for (i = 0; i < a; i++)
			for (j = 0; j < b; j++)
				for (k = 0; k < c; k++)
					scanf("%d", &map[i][j][k]);
		ans = bfs(0, 0, 0);
		printf("%d\n", ans);
	}

	return 0;
}