网络流24题--方格取数问题
若有疏漏,敬请指出不足之处,谢谢!!!
最近刷了网络流的不少题目,,,所以决定总结一下关于方格取数问题的基本做法。
模版题 Hdu 1565
题意
大概的题意是:
给你一个n*n的格子的棋盘,每个格子里面有一个非负数。
从中取出若干个数,使得任意的两个数所在的格子没有公共边,就是说所取的数所在的2个格子不能相邻,并且取出的数的和最大。
Hdu 1565就是这样的题目。
通常做法
对于这类题目,甚至可以推广到只要有方格类的。我们可以考虑将其黑白染色,如图,

假设其点权为2,1,3,4,作为一个例子
方格就转化为二分图,相邻的格子连边,求最大点权独立集。
知识原理和定义
最大点权独立集的定义是,在二分图中选定一些点,使这些点不被边直接相连的同时满足点权和最大。
最小点权覆盖是指,在二分图中选定一些点,使这些点能够覆盖所有边,即满足所有边的其中一个点是选定点的一个。
众所周知(在这里就不证明了),最大点权独立集等于点权和减去最小点权覆盖,你们可以试验一下。
也就是在二分图中选定若干点后满足最小点权覆盖,没选定的点即构成最大点权独立集。
对于解决最小点权覆盖,采用最小割方式解决,网络流通常是把限制条件转化成边权来跑。
建图
所以构造源点,连接源点和被染成黑色的点,边权为该点的点权,相邻的点边权为inf
如图:
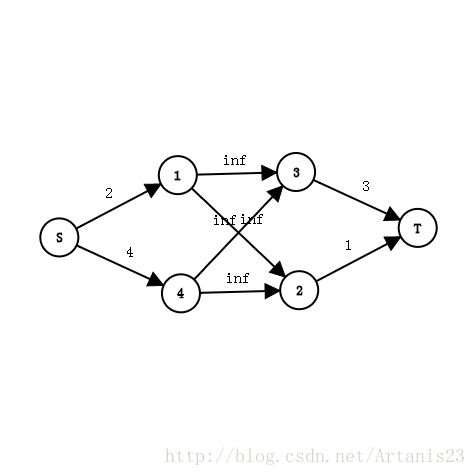
建图思路
然后求最小割,就是最小点权覆盖
证明如下:
我们知道如果存在最小割,那么任何形如S-u-v-T的线路上必定是不通的(即有割从中经过,否则不满足割的性质)
因为是求最小割,而u-v的边权是inf,因此割不会从此经过,也就是从
S-u,v-T中选一个经过。
选了一条边之后,边上除了源点和汇点的另外一个点即视为选中,
所以当有割时,任意一个S-u-v-T的线路肯定是u或者v被选中,
也就是满足所有边都覆盖。
当是最小割时,点权覆盖也为最小。
所以最小割=最小点权覆盖,
同时又最大流最小割定理可知,最大流=最小割,所以这类题目可以跑一下网络流最大流来完成。
AC代码
Hdu 1565代码如下:
#include 1,j),inf);
addEdge(cal(i+1,j),tmp,0);
}
if(j>1){
addEdge(tmp,cal(i,j-1),inf);
addEdge(cal(i,j-1),tmp,0);
}
if(j1),inf);
addEdge(cal(i,j+1),tmp,0);
}
} else{
addEdge(tmp,T,a[i][j]);
addEdge(T,tmp,0);
}
}
}
while(bfs()){
memcpy(work,head,sizeof(head));
while(flow=dfs(S,inf)){
ans += flow;
}
}
printf("%d\n",sum-ans);
}
} 进阶题Hdu 1569
还有Hdu 1569也是几乎完全一模一样的,只不过由n*n的方格改为
n*m罢了,没有什么区别,注意下细节就行了。
Hdu 3820则是一道值得一做的拓展题了。
题意
题意是给一个方格阵,每个方格可以放金蛋或者银蛋,放不同的蛋会分别拿到各自的分数,
但是,如果相邻的方格颜色一样,如果都是金色,就需要减掉G,否则减掉S,
现在求最大分数。
建图
其实这道题是方格取数的加强版,道理是一样的。
将所有方格黑白染色,
因为一个方格有金银两个状态,所以可以通过拆点的方法来做,
为了便于说明,定义黑 为黑色方格放金蛋的点,黑’为放银蛋,白为白色方格放金蛋,白’为银色
tips:拆点是网络流最基本的方法,必须要掌握。
为构造图使满足相同颜色的约束条件,所以黑 必须连接 白,而黑安排在左边,所以白安排在右边
所以源点连接黑,边权为该方格分数,也连接白’
黑‘->T,白->T
但为什么不能够源点连黑、黑’,白、白‘连汇点呢?解释如下
建图思路
首先肯定要黑连接黑’,权值为inf,使得黑和黑’只能选择一个,道理和前面的方格取数一样,这样的话即指黑和黑’之间存在边。
注意到一个细节,我们要转化成最大点权独立集,而是存在于二分图中的,如果黑、黑‘在二分图同一边,它们存在边,与二分图定义矛盾。
然后白’也连接白
此时黑连接白,权值为G,
因为我们知道求最大分数是求最大点权独立集=总点权-最小点权覆盖,
所以最小点权覆盖选择的边,就是最大点权独立集不选的边,
而最小点权覆盖=最小割,
所以最小割选择的边中不包括S、T的点就等于最小点权覆盖所需的点。
以一个图来做例子(题目中的第一个样例):
建图后如图所示:
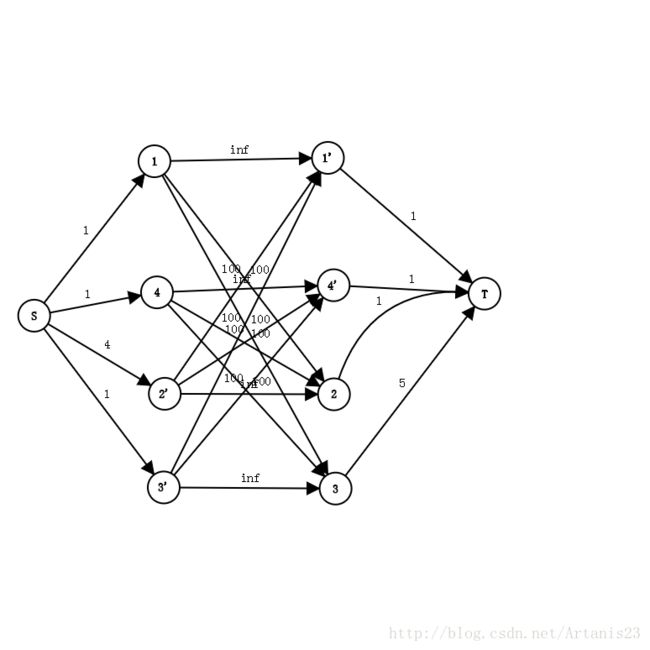
经计算可以知道,最小割为以下红色的边:

那么也就是只需要选择1、4、3、1‘、4’、2就能实现完全覆盖,
所以选2‘、3构成最大点权独立集。
所以所以所有点中不包括最小割经过的边中不包括S、T的点的点,是最大点权独立集的点
因为最大点权独立集=点权和-最小割,
而相邻方格取同样颜色是要减去费用的,也就是可以体现在最小割上,所以可以通过构造边来实现,
最后,可以再次考虑一个S-u-v-T的路径,其中u,v代表相同颜色(金银)且相邻的方格。
那么这条路径由于割的性质不能够联通,
因此最小割只能经过S-u,v-T的其中一条边,或者经过u-v的边
这就意味着:
两个相邻的方格,如果要选同样颜色(金银),要不在两个当中只选一个,否则两个都选的话,就得多花费用(u-v边权)
这样就能够满足题意了,题目也就能够解决了。
代码
代码如下:
#include