题意:
有一颗n个叶子的无权树,输入两两叶子的距离,恢复出这棵树并输出每个非叶子节点的度数。
思路:
参考:https://blog.csdn.net/zju2016/article/details/78450509
无根树,现将一个叶子节点作为根。逐个探测剩下的叶子节点,并在这个过程中不断增加内部节点以满足其距离要求,最终建树完成。
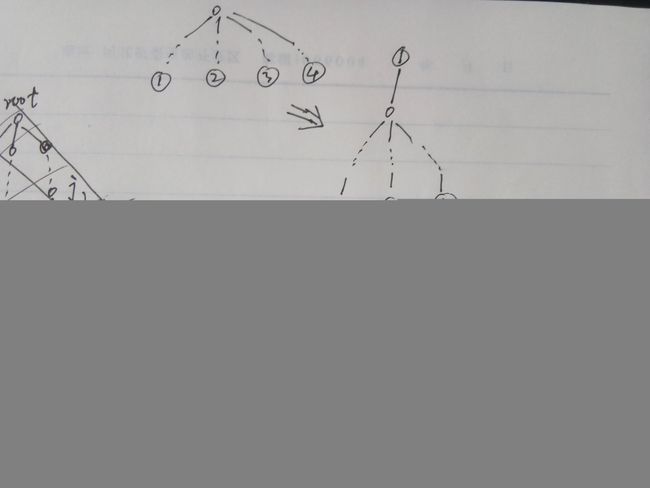
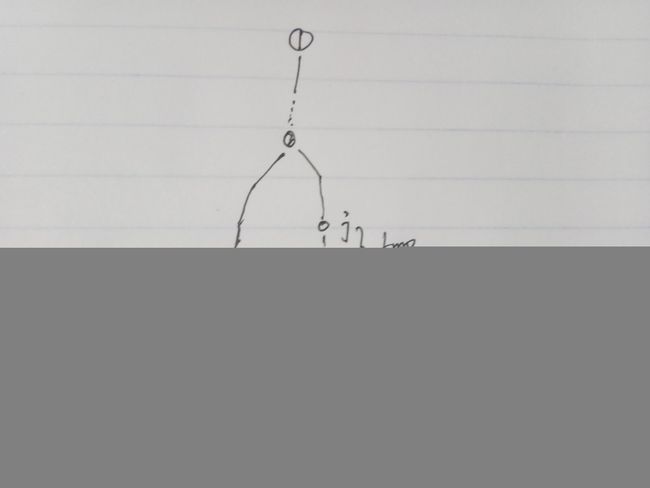
内部节点 j 的选择:
逐步测试是否能够找到某个内部的节点,使得该内部节点到所有的已经加入的外部节点的距离与待加入的外部节点的距离之差(tmp)相等,如果找到,就保存差值,逐步扩展并且计算扩展的点到已加入的外部节点的距离,计算其度数。
#include
#include
#include
#define fi first
#define se second
#define pii pair
using namespace std;
const int INF = 0x3f3f3f3f;
typedef long long LL;
const int maxn = 2000+5;
int n, idx, dis[maxn][maxn], a[55][55], deg[maxn], id[55];
void Build(){
id[1] = ++idx; dis[1][1] = 0;
for(int i = 2; i <= n; ++i){
int u, last, tmp;
for(int j = 1; j <= idx; ++j){
tmp = a[i][1] - dis[j][1];
int fg = 0;
for(int k = 2; k < i; ++k) if(a[i][k] - dis[j][id[k]] != tmp){fg = 1; break;}
if(!fg){last = j; break;}
}
for(int j = 1; j <= tmp; ++j,last = u){
deg[u = ++idx] = 0; dis[u][u] = 0;
++deg[last]; ++deg[u];
for(int k = 1; k < idx; ++k) dis[u][k] = dis[k][u] = dis[k][last] + 1;
}
id[i] = idx;
printf("idx = %d, ",idx);
}puts("");
}
int main()
{
freopen("in.txt","r",stdin);
while(scanf("%d",&n) == 1&&n){
for(int i = 1; i <= n; ++i) for(int j = 1; j <= n; ++j) scanf("%d",&a[i][j]);
idx = 0; memset(deg, 0, sizeof(deg));
Build();
sort(deg+1, deg+idx+1);
for(int i = 1; i <= idx; ++i){
if(deg[i] == 1) continue;
printf("%d",deg[i]);
if(i != idx) printf(" ");
}
printf("\n");
}
return 0;
}
书上的思路是递归建树:
#include
#include

