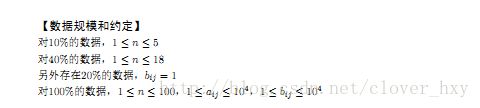SDOI2017 Round1解题报告
虽然考的很差，很不想去再面对这套题，但是只有直面失败才能走向成功。从新审视这套题，才发现自己存在的问题和差距。
Day 1
T1
题解
mobius反演。。。
∏ni=1∏mj=1fi[gcd(i,j)]
∏nk=1fi[k]∑ni=1∑mj=1[gcd(i,j)=k]
设 f(d)=∑ni=1∑mj=1[gcd(i,j)=k] ,表示最大公约数为k的数对数
F(d)=⌊nd⌋∗⌊md⌋ 表示公约数为k的数对数
根据莫比乌斯反演的公式 f(d)=∑d|nμ(nd)∗F(n)
所以式子可以变成
∏k=1nfi[k]∑ni=1μ(i)∗⌊nk∗i⌋∗⌊mk∗i⌋
,当时考试的时候就化简到这一步，然后设
g(x,y)=∑ni=1μ(i)∗⌊xi⌋∗⌊yi⌋ ,
x=⌊nk⌋,y=⌊mk⌋ ,直接根号套根号的做，TLE了4组。
但是实际上式子还能进一步的化简，设 T=i∗k
∏T=1n(∏d|nfi[d]μ(Td))⌊nT⌋∗⌊mT⌋
设 h(T)=∏d|nfi[d]μ(Td) ，如果 h(T) 可以预处理，那么回答询问的时间复杂度就是 O(n√+m−−√) 。发现 h(T) 的求解与T的约数有关，可以用艾氏筛法 O(nlog2n) 的求，其中一个 logn 是快速幂的。
我们预处理出 h(T) 的前缀积和前缀积的逆元，就可以搞啦。
有一点需要特别注意： a(p−1)=1(mod p) p 是质数,所以所有的指数是对 (p−1) 取模，考试的时候脑残，因为这个原因丢了30分，想想就心疼。。。
代码
#includeT2
题解
LCT+线段树
感觉自己对LCT一直有抵触情绪。。。。所以决定好好写这道题的题解。
一条路径的权值为：路径上的颜色种类和。
我们定义f(x)，表示x与fa[x]的颜色是否相同，相同为0，不同为1，令 f(1)=1。g(x)表示x到root路径上的f的和。然后考虑怎么维护g(x)。
因为是一颗有根树，所以我们不牵扯到换根操作，最初的时候所以的节点都是指向他的父节点的。(儿子认父亲，父亲不认儿子)。lct维护的splay中的信息，一定是一条重链的信息。对于这条链来说，splay中所有节点的颜色都是相同的。
现在我们要将x到root的路径染成一种新的颜色，利用access操作实现对节点的修改。
access中有一个砍重儿子的过程，对于上图中的三号紫点来说，砍掉了四号紫点(不是单独的一个点，而是四号紫点所在的splay)，对于四号紫点所在的splay维护的重链的链顶节点(就是三号紫点真正的儿子)来说，他子树中的所有点g值都会增加1。
现在一号蓝点变成了三号紫点的重儿子，那么对应的一号蓝点所在的splay维护的重链的链顶节点子树中所有点的g值都减少1.
根据access的过程假设当前点是三号紫点，那么他与root在一棵splay中，转根后他就是splay的根，fa[x]就是0，不在需要更改任何g的值。我们发现对于1-3号紫点他们的g值在染色过程中是不发生改变的，所以可以用lct科学的维护。
那么g值得改变都是针对子树的，所以我们搞出dfs序，那么每次修改都是修改的一段区间，就变成了线段树的区间修改。
对于操作3，直接进行区间查询即可。
对于操作2，x->y 的答案就是g(x)+g(y)-2*g(lca(x,y))+1,进行三次单点查询。
代码
#include
r[t]=max(r[t],r[x]);
if (x==rt) break;
x=t;
}
}
}
int lca(int x,int y)
{
if (deep[x]int k=deep[x]-deep[y];
for (int i=0;i<=17;i++)
if ((k>>i)&1) x=f[x][i];
if (x==y) return x;
for (int i=17;i>=0;i--)
if (f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
return f[x][0];
}
void update(int now)
{
tr[now]=max(tr[now<<1],tr[now<<1|1]);
}
void pushdown(int now)
{
if (delta[now]) {
tr[now<<1]+=delta[now]; tr[now<<1|1]+=delta[now];
delta[now<<1]+=delta[now]; delta[now<<1|1]+=delta[now];
delta[now]=0;
}
}
void qjchange(int now,int l,int r,int ll,int rr,int val)
{
if (ll<=l&&r<=rr) {
tr[now]+=val; delta[now]+=val;
return;
}
int mid=(l+r)/2;
pushdown(now);
if (ll<=mid) qjchange(now<<1,l,mid,ll,rr,val);
if (rr>mid) qjchange(now<<1|1,mid+1,r,ll,rr,val);
update(now);
}
int find(int now,int l,int r,int x)
{
if (l==r) return tr[now];
int mid=(l+r)/2;
pushdown(now);
if (x<=mid) return find(now<<1,l,mid,x);
else return find(now<<1|1,mid+1,r,x);
}
int query(int now,int l,int r,int ll,int rr)
{
if (ll<=l&&r<=rr) return tr[now];
int mid=(l+r)/2; int ans=0;
pushdown(now);
if (ll<=mid) ans=max(ans,query(now<<1,l,mid,ll,rr));
if (rr>mid) ans=max(ans,query(now<<1|1,mid+1,r,ll,rr));
return ans;
}
bool isroot(int x)
{
return ch[fa[x]][1]!=x&&ch[fa[x]][0]!=x;
}
int get(int x)
{
return ch[fa[x]][1]==x;
}
void rotate(int x)
{
int y=fa[x]; int z=fa[y]; int which=get(x);
if (!isroot(y)) ch[z][ch[z][1]==y]=x;
fa[x]=z; fa[y]=x; ch[y][which]=ch[x][which^1];
fa[ch[x][which^1]]=y; ch[x][which^1]=y;
}
void splay(int x)
{
int y;
while (!isroot(x)){
y=fa[x];
if (!isroot(y)) rotate(get(y)==get(x)?y:x);
rotate(x);
}
}
int get_root(int x)
{
while (ch[x][0]) x=ch[x][0];
return x;
}
void access(int x)
{
int t=0;
while (x) {
col[x]=k;
splay(x);
int t1=get_root(ch[x][1]);
if (t1) qjchange(1,1,n,l[t1],r[t1],1);
ch[x][1]=t;
int t2=get_root(t);
if (t2) qjchange(1,1,n,l[t2],r[t2],-1);
t=x; x=fa[x];
}
}
int main()
{
freopen("paint.in","r",stdin);
freopen("paint.out","w",stdout);
scanf("%d%d",&n,&m); k=n; mi[0]=1;
for (int i=1;i<=18;i++) mi[i]=mi[i-1]*2;
for (int i=1;iint x,y; scanf("%d%d",&x,&y);
add(x,y);
}
dfs(1);
for (int i=1;i<=n;i++) qjchange(1,1,n,l[i],r[i],1);
for (int i=1;i<=m;i++) {
int opt,x,y; scanf("%d%d",&opt,&x);
if (opt==1) k++,access(x);
if (opt==2) {
scanf("%d",&y); int t=lca(x,y);
printf("%d\n",find(1,1,n,l[x])+find(1,1,n,l[y])-2*find(1,1,n,l[t])+1);
}
if (opt==3) printf("%d\n",query(1,1,n,l[x],r[x]));
}
} T3
题解
DP+矩阵乘法
至少有一个数是质数的方案数=无限制的方案数-只有质数的方案数
预处理出转移矩阵，直接上矩阵快速幂即可。
代码
#include//for (int i=0;i" "; cout<// for (int i=0;i" "; cout<for (int i=0;ifor (int j=0;j0;
}
data mul(data a,data b)
{
data c;
for (int i=0;ifor (int j=0;j0;
for (int k=0;k*b.a[k][j]%mod)%mod;
}
return c;
}
data quickpow(data num,int x){
data base=num; data ans=c;
while (x) {
if (x&1) ans=mul(ans,base);
x>>=1;
base=mul(base,base);
}
return ans;
}
LL solve(int a[])
{
clear(e);
for (int i=0;ifor (int j=0;j%p]+=a[j],e.a[i][(i+j)%p]%=mod;
data ans=quickpow(e,n);
return ans.a[0][0];
}
int main()
{
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
scanf("%d%d%d",&n,&m,&p);
init();
for (int i=0;i1;
LL t=solve(a)-solve(b);
printf("%I64d\n",(t%mod+mod)%mod);
} Day 2
T1
题解
01分数规划+费用流。
看到 C=a′1+a′2+...+a′nb′1+b′2+...+b′n 就应该想到01分数规划。
先考虑如果每两个人之间只有一个有关的权值该怎么做？那么问题就变成了最大权匹配。这个貌似有一个叫做KM的算法可以快速求解，但是费用流也很好用啊。
S−>i 容量为1，费用为0
j−>T 容量为1，费用为0
i−>j 容量为1，费用为 val[i][j]
二分答案，然后将边权赋值成 a[i][j]−mid∗b[i][j] ,跑最大费用最大流，如果最后的费用为正，说明答案还可以更大。
据学长说，把double运算变成整数运算会快哦。
代码
#includeint now=q[++head];
for (int i=point[now];i!=-1;i=nxt[i])
if (dis[v[i]]last[v[i]]=i;
if (!can[v[i]]) {
can[v[i]]=1;
q[++tail]=v[i];
}
}
can[now]=0;
}
if (dis[t]==-inf) return false;
int flow=addflow(s,t);
ans+=dis[t]*flow;
return true;
}
void solve(int s,int t)
{
while (spfa(s,t));
}
bool check(double mid)
{
tot=-1;
memset(point,-1,sizeof(point));
S=1; T=2*n+2;
for (int i=1;i<=n;i++) add(S,i+1,1,0);
for (int i=1;i<=n;i++) add(i+n+1,T,1,0);
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++) add(i+1,j+n+1,1,a[i][j]-mid*b[i][j]);
//cout<0; solve(S,T);
return ans>=-eps;
}
int main()
{
freopen("ball.in","r",stdin);
freopen("ball.out","w",stdout);
scanf("%d",&n); double sum=0;
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++) scanf("%lf",&a[i][j]),sum=max(sum,a[i][j]);
for (int i=1;i<=n;i++)
for (int j=1;j<=n;j++) scanf("%lf",&b[i][j]);
double l=0; double r=sum; double ans=0;
while (r-l>=eps) {
double mid=(l+r)/2;
if (check(mid)) ans=max(ans,mid),l=mid+eps;
else r=mid-eps;
}
printf("%.6lf\n",ans);
} T2
题解
KMP+高斯消元
设N为未结束状态的概率。
假设用两个串TTH和HTT，设第一个获胜的概率是A,第二个人获胜的概率为B
如果在N后面加上TTH,那么有三种可能
NTTH=A+BTH+BH ,是什么意思呢？就是如果在N后面加入TTH，那么第一个人猜的序列出现在了硬币序列中，第一个人获胜，但是N是什么我们不清楚，但是有可能到达第一个T或者第二个T的时候第二个人就获胜了。
所以对于状态NTTH，可以由三个状态得到。
123N=A+12B+122B，12 表示的是正反面的概率。
这样我们得到了n个方程，但是有n+1个未知量，因为所有人获胜的总概率是1，那么我们加入这个方程就成功得到了n+1个未知量，n+1个方程。高斯消元直接解就可以了
那么我们怎么得到每个串之间类似A,B的关系呢？发现满足A的前缀是B的后缀，这不就是失配的定义么。所以直接将两个串连起来，用KMP求失配即可。系数就是 12m−末位失配 ,需要注意的是系数应该是末位失配一直沿着fail指针向前跳，经过的所有点的概率和。
代码
#includefor (int i=1;i<=n;i++) a[i][n+1]=-p;
for (int i=1;i<=n;i++) a[n+1][i]=1.0;
b[n+1]=1;
gauss(n+1);
for (int i=1;i<=n;i++) printf("%.7lf\n",ans[i]);
} T3
题解
线段树
首先对a的求解式子进行变形
a=∑Ri=L(xi−x¯)∗(yi−y¯)∑Ri=L(xi−x¯)2
a=∑Ri=Lxi∗yi−x¯∗yi−y¯∗xi+x¯∗y¯∑Ri=Lxi2+x¯2−2∗x¯∗xi
其实上面式子的计算就变成了好几部分，我们可以用线段树分开维护一下。
sumx 区间[l,r]中所有xi的和
sumy 区间[l,r]中所有yi的和
xy 区间[l,r]中所有xi*yi的和
sq 区间中所有xi^2的和
squ ∑Ri=Li2
sum ∑Ri=Li
tagx 针对x的区间增加标记
tagy 针对y的区间增加标记
cx 针对x的区间覆盖标记
cy 针对y的区间覆盖标记
上面式子中的 x¯,y¯ 都可以通过区间查询后计算。 x¯=sumx(R−L+1),y¯=sumy(R−L+1)
设 len=R−L+1 ,那么
a=xy−x¯∗sumy−y¯∗sumx+len∗x¯∗y¯sq+len∗x¯−2∗x¯∗sumx
说几个主要的维护过程吧
(1) (x+s)(y+t)=xy+sy+tx+st
对应到线段树中的修改 xy=xy+sumx∗t+sumy∗s+len∗s∗t
(2) x−>s+i,y−>t+i
对应到线段树中的修改 sumx=len∗s+sum,sumy=len∗t+sum
sq=s∗s∗len+squ+2∗s∗sum
xy=s∗t∗len+squ+(s+t)∗sum
(3)增加标记与覆盖标记的冲突
如果是覆盖标记遇到加法标记，覆盖标记正常打，增加标记清零
如果是增加标记遇到覆盖标记，就将增量直接加给覆盖标记
写的过程中有一个小细节需要注意，就i*i可能会炸int，注意加强转啊！！！
代码
#include
#include
#include
#include
#include
#define N 200003
#define eps 1e-9
#define inf 1000000000
using namespace std;
struct data {
double sumx,sumy,xy,sq,sum,squ;
double tagx,tagy,cx,cy;
}tr[N*4];
double xi[N],yi[N];
int n,m;
data update(data l,data r)
{
data now; now.tagx=now.tagy=0;
now.cx=now.cy=inf;
now.sumx=l.sumx+r.sumx;
now.sumy=l.sumy+r.sumy;
now.xy=l.xy+r.xy;
now.sq=l.sq+r.sq;
now.squ=l.squ+r.squ;
now.sum=l.sum+r.sum;
return now;
}
void build(int now,int l,int r)
{
if(l==r) {
tr[now].sumx=xi[l]; tr[now].sumy=yi[l];
tr[now].xy=xi[l]*yi[l]; tr[now].sq=xi[l]*xi[l];
tr[now].sum=l; tr[now].squ=(double)l*(double)l;
return;
}
int mid=(l+r)/2;
build(now<<1,l,mid);
build(now<<1|1,mid+1,r);
tr[now]=update(tr[now<<1],tr[now<<1|1]);
}
void calc(int now,int l,int r,double valx,double valy)
{
double len=(r-l+1);
tr[now].tagx+=valx; tr[now].tagy+=valy;
tr[now].sq+=len*valx*valx+2.0*valx*tr[now].sumx;
tr[now].xy+=valx*tr[now].sumy+valy*tr[now].sumx+valx*valy*len;
tr[now].sumx+=valx*len; tr[now].sumy+=valy*len;
if (tr[now].cx==inf&&tr[now].cy==inf) return;
tr[now].cx+=valx; tr[now].cy+=valy;
tr[now].tagx=tr[now].tagy=0;
}
void cover(int now,int l,int r,double valx,double valy)
{
double len=(r-l+1);
tr[now].cx=valx; tr[now].cy=valy; tr[now].tagx=tr[now].tagy=0;
tr[now].sq=tr[now].squ+tr[now].sum*2.0*valx+valx*valx*len;
tr[now].xy=tr[now].squ+(valx+valy)*tr[now].sum+valx*valy*len;
tr[now].sumx=tr[now].sum+len*valx;
tr[now].sumy=tr[now].sum+len*valy;
}
void pushdown(int now,int l,int r)
{
int mid=(l+r)/2;
if (tr[now].cx!=inf||tr[now].cy!=inf){
cover(now<<1,l,mid,tr[now].cx,tr[now].cy);
cover(now<<1|1,mid+1,r,tr[now].cx,tr[now].cy);
tr[now].cx=tr[now].cy=inf;
}
if (fabs(tr[now].tagx)>=eps||fabs(tr[now].tagy)>=eps) {
calc(now<<1,l,mid,tr[now].tagx,tr[now].tagy);
calc(now<<1|1,mid+1,r,tr[now].tagx,tr[now].tagy);
tr[now].tagx=0; tr[now].tagy=0;
}
}
data query(int now,int l,int r,int ll,int rr)
{
if (ll<=l&&r<=rr) return tr[now];
int mid=(l+r)/2;
pushdown(now,l,r); data ans; bool pd=false;
if (ll<=mid) ans=query(now<<1,l,mid,ll,rr),pd=true;
if (rr>mid) {
if (pd) ans=update(ans,query(now<<1|1,mid+1,r,ll,rr));
else ans=query(now<<1|1,mid+1,r,ll,rr);
}
return ans;
}
void qjchange(int now,int l,int r,int ll,int rr,double valx,double valy)
{
if (ll<=l&&r<=rr) {
calc(now,l,r,valx,valy);
return;
}
int mid=(l+r)/2;
pushdown(now,l,r);
if (ll<=mid) qjchange(now<<1,l,mid,ll,rr,valx,valy);
if (rr>mid) qjchange(now<<1|1,mid+1,r,ll,rr,valx,valy);
tr[now]=update(tr[now<<1],tr[now<<1|1]);
}
void qjcover(int now,int l,int r,int ll,int rr,double valx,double valy)
{
if (ll<=l&&r<=rr) {
cover(now,l,r,valx,valy);
return;
}
int mid=(l+r)/2;
pushdown(now,l,r);
if (ll<=mid) qjcover(now<<1,l,mid,ll,rr,valx,valy);
if (rr>mid) qjcover(now<<1|1,mid+1,r,ll,rr,valx,valy);
tr[now]=update(tr[now<<1],tr[now<<1|1]);
}
int main()
{
freopen("relative.in","r",stdin);
freopen("relative.out","w",stdout);
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) scanf("%lf",&xi[i]);
for (int i=1;i<=n;i++) scanf("%lf",&yi[i]);
build(1,1,n);
for (int i=1;i<=m;i++) {
int opt,l,r; scanf("%d",&opt);
if (opt==1) {
scanf("%d%d",&l,&r);
data a=query(1,1,n,l,r); double len=r-l+1;
double ans=0,ans1=0; double bx=a.sumx/len; double by=a.sumy/len;
ans=a.xy-bx*a.sumy-by*a.sumx+bx*by*len;
ans1=len*bx*bx+a.sq-2.0*bx*a.sumx;
printf("%.10lf\n",ans/ans1);
}
if (opt==2){
double s,t;
scanf("%d%d%lf%lf",&l,&r,&s,&t);
qjchange(1,1,n,l,r,s,t);
}
if (opt==3) {
double s,t; scanf("%d%d%lf%lf",&l,&r,&s,&t);
qjcover(1,1,n,l,r,s,t);
}
}
}