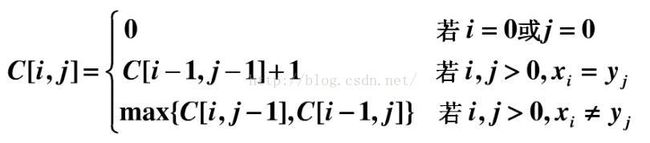动态规划(最长公共子序列/最大字段和/最大子矩阵和)

DP基本思想：将求解的问题分解成若干子问题，先求解子问题，再从这些子问题得到原问题的解。

DP的两个基本要素（重要性质）：

1. 最优子结构性质。即问题的最优解包含了其子问题的最优解。

2. 重叠子问题性质。有的子问题可能会被计算多次。因此采用备忘录方法避免对相同子问题的重复求解。

DP编程关键：状态转移方程、边界条件

最长公共子序列(LCS)

Description: 
给两个长度为n的全排列，求其最长公共子序列长度。 
Input: 
第一行是一个正整数N，表示全排列长度。 
第二行有n个整数，保证是一个n的全排列。 
第三行有n个整数，保证是一个n的全排列。 
Output: 
输出第一行有一个整数，表示两数组最长公共子序列长度。 
Sample Input: 
5 
1 3 2 4 5 
5 2 3 1 4 
Sample Output: 
2 

 

#include
#include
#include
using namespace std;
const int MAX = 1e3+7;
int dp[MAX][MAX]; 
int str1[MAX],str2[MAX];
int main(void){
	int n;
	while(cin>>n){
		for(int i=1;i<=n;i++) cin>>str1[i];
		for(int i=1;i<=n;i++) cin>>str2[i];
		memset(dp,0,sizeof(dp));
		for(int i=0;i<=n;i++){
			for(int j=0;j<=n;j++){
				if(i==0||j==0) dp[i][j]=0;
				else if(str1[i]==str2[j]) dp[i][j]=dp[i-1][j-1]+1;
				else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
			}
		}
		cout<

Coincidence

题目描述

Find a longest common subsequence of two strings.

输入描述:

First and second line of each input case contain two strings of lowercase character a…z. There are no spaces before, inside or after the strings. Lengths of strings do not exceed 100.

输出描述:

For each case, output k – the length of a longest common subsequence in one line.

输入

abcd
cxbydz

输出

2

和上面的题其实完全一样。

#include
#include
using namespace std;
const int MAX =105;
int dp[MAX][MAX];
int max(int a,int b){
	return a>b?a:b; 
}
int main(void)
{
	char a[105],b[105];
	while(scanf("%s%s",&a,&b)!=EOF){
		int a_len = strlen(a);
		int b_len = strlen(b);
		memset(dp,0,sizeof(dp));
		for(int i=1;i<=a_len;i++){
			for(int j=1;j<=b_len;j++){
				if(a[i-1]==b[j-1]) dp[i][j]=dp[i-1][j-1]+1;
				else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
			} 
		}
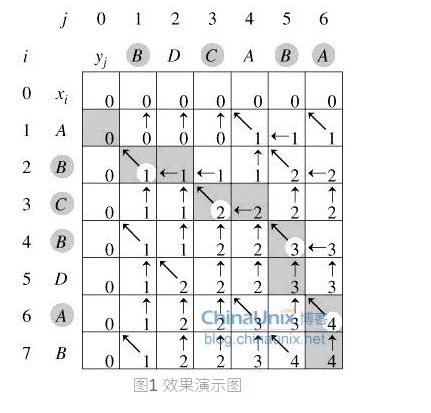
		cout<

如果要求找出这个最长公共子序列是什么呢？考虑记录每一次的转移方向。

思路：用flag[][]记住当前状态是从什么方向转移而来的，然后从flag[n][n]开始进行回溯。如果flag[i][j]==0，则说明此时str1[i]==str2[j]，状态dp[i][j]是从dp[i-1][j-1]转移而来的，此时打印出这个字符。

#include
#include
#include
using namespace std;
const int MAX = 1e3+7;
int dp[MAX][MAX]; 
int flag[MAX][MAX];
int str1[MAX],str2[MAX];
void printSeq(int i,int j)
{
	if(i==0||j==0) return;
	if(flag[i][j]==0){	//该位置从左上方转移而来，说明出现了str1[i]==str2[j] 
		cout<>n){
		for(int i=1;i<=n;i++) cin>>str1[i];
		for(int i=1;i<=n;i++) cin>>str2[i];
		memset(dp,0,sizeof(dp));
		memset(flag,0,sizeof(flag)); 
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				if(str1[i]==str2[j]){
					dp[i][j]=dp[i-1][j-1]+1;
					flag[i][j]=0;//表示从左上方转移而来 
				} 
				else
				{
					if(dp[i-1][j]>dp[i][j-1]){
						dp[i][j]=dp[i-1][j];
						flag[i][j]=1;//表示从上方转移而来 
					} 
					else{
						dp[i][j]=dp[i][j-1];
						flag[i][j]=-1;//表示从左方转移而来 
					}
				}
				//dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
			}
		}
		cout<

最大字段和

Description:

给出一段序列，选出其中连续且非空的一段使得这段和最大。

Input:

第一行是一个正整数N（N <= 200000），表示了序列的长度。

第接下来的N行包含N个绝对值不大于10000的整数A[i]，描述了这段序列。

Output:

仅包括1个整数，为最大的子段和是多少。子段的最小长度为1。

Sample Input:

7

2 -4 3 -1 2 -4 3

Sample Output:

4

#include 
using namespace std;
int a[200001];
int main(void)
{
	int n;
	scanf("%d",&n);
	for(int i=0;i0?b+a[i]:a[i];
		if(b>max) max = b;
	}
	printf("%d\n",max);
	return 0;
 } 

记录首尾的最大字段和

题目描述

    给定K个整数的序列{ N1, N2, ..., NK }，其任意连续子序列可表示为{ Ni, Ni+1, ..., Nj }，其中 1 <= i <= j <= K。最大连续子序列是所有连续子序列中元素和最大的一个，例如给定序列{ -2, 11, -4, 13, -5, -2 }，其最大连续子序列为{ 11, -4, 13 }，最大和为20。现在增加一个要求，即还需要输出该子序列的第一个和最后一个元素。

输入描述:

测试输入包含若干测试用例，每个测试用例占2行，第1行给出正整数K( K< 10000 )，第2行给出K个整数，中间用空格分隔。当K为0时，输入结束，该用例不被处理。

输出描述:

对每个测试用例，在1行里输出最大和、最大连续子序列的第一个和最后一个元素，中间用空格分隔。如果最大连续子序列不唯一，则输出序号i和j最小的那个（如输入样例的第2、3组）。若所有K个元素都是负数，则定义其最大和为0，输出整个序列的首尾元素。

输入

6
-2 11 -4 13 -5 -2
10
-10 1 2 3 4 -5 -23 3 7 -21
6
5 -8 3 2 5 0
1
10
3
-1 -5 -2
3
-1 0 -2
0

输出

20 11 13
10 1 4
10 3 5
10 10 10
0 -1 -2
0 0 0

 说明：虽然AC但可能不太优雅。另外此题可以暴力求解。

参考链接：https://www.nowcoder.com/questionTerminal/afe7c043f0644f60af98a0fba61af8e7

#include
#include
#define MIN 0x3f3f3f3f
using namespace std;
int dp[10001];
int a[10001];
int main(void)
{
	int n;
	while(cin>>n)
	{
		if(n==0) break;
		memset(dp,0,sizeof(dp));
		memset(a,0,sizeof(a));
		for(int i=1;i<=n;i++){
			cin>>a[i];
		}
		int max = 0;
		int start=1;
		int startIndex=1,endIndex=1;
		dp[1]=a[1];
		bool flag=false;
		for(int i=1;i<=n;i++){
			if(a[i]>=0) flag=true;
			if(dp[i-1]>0) dp[i]=dp[i-1]+a[i];
			else {
				dp[i]=a[i];
				start=i;
			}
			if(dp[i]>max){
				max = dp[i];
				startIndex=start;
				endIndex=i;
			}
		}
		if(!flag) cout<

最大子矩阵和（最大字段和升级版）

思路：对于，把每一列的start到end之间的元素加起来，再用最大字段和。

//最大子矩阵和
//经验教训
//i,j尽量留给数组下标
//尽量用实际含义来命名变量 
#include
#include 
#include
#define MIN 0x80000000
using namespace std;
int arr[101][101];
int total[101];
int n,m,size;
int  maxArraySum(int a[],int n){
	int b=MIN;int max=MIN;
	for(int i=0;i0) b=b+a[i];
		else b=a[i];
		if(b>max) max=b;
	}
	return max;
} 
int main(void)
{
	while(scanf("%d",&size)!=EOF){
		int n=size;
		int m=size; 
		memset(arr,0,sizeof(arr));
		memset(total,0,sizeof(total));
		for(int i=0;ians) ans=thismax;
			}
		}
		printf("%d\n",ans);
	}
	return 0;
}

参考链接：https://blog.csdn.net/weixin_40170902/article/details/80585218