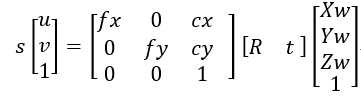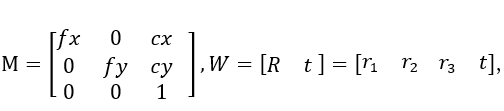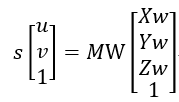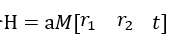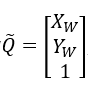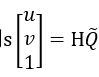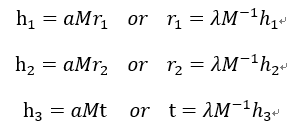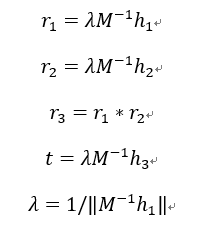相机标定的数学原理及其推导过程
接着上一篇博客计算机视觉之相机模型推导建立过程
在上一篇博客中介绍了针孔模型,这篇博客介绍一下相机的畸变参数,然后对推导过程做了详细的推导。
畸变参数:由于针孔模型透光很少,导致相机的曝光时间很长,现实生活中一般使用凸透镜代替针孔,大大提高了曝光效率,但是代价便是引入了畸变。畸变主要分为两种,切向畸变和径向畸变。
径向畸变:由于一般透镜在制作过程中,由于工艺问题,所以光在离中心越远的地方折射的角度会越大,导致成像就是产生了"鱼眼"效果,导致了径向畸变,如图所示。一般来说,贵一点的镜头径向畸变的影响会小一点。可以采用泰勒级数展开式来矫正,至于为什么,由于知识较少,无法解释。
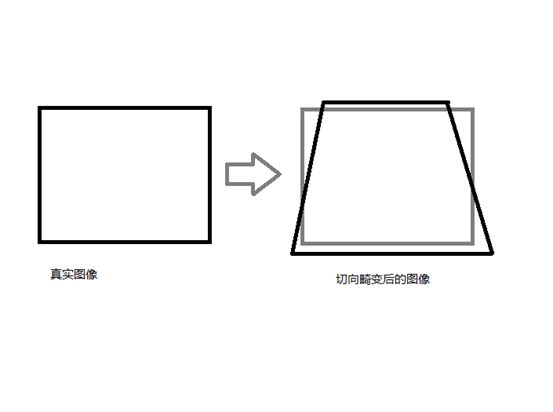
切向畸变:由于镜头在装配过程中没法保证凸透镜和成像面绝对的平行,所以会产生切向畸变,具体表现就是
图像有点夸张,不过大概是这个样子。同样切向畸变可以通过公式矫正,同样没法解释为什么要用这个来矫正。
到目前为止,我们介绍了比较完整的相机模型,接下来开始推导求解内参数矩阵K和畸变参数k和p的过程,这个过程也称为相机内参数的标定。至于相机的外参数R和t是在每一个场景都会发生变化的,所以内参数才是所追求的不变的东西,但是标定过程中也会涉及到外参数。
内参数的重要性:在立体视觉中,所有的计算都是建立在内参数的基础上的,所以要保证内参数尽可能的精确,一般会进行标定。接下来介绍张正友标定法,也就是常见的使用标定板标定,这里介绍他的原理。
单应性
在计算机视觉中,平面的单应性被定义为从一个平面到另一个平面的投影映射。因此一个二维平面的点映射到摄像机成像仪上的映射就是平面单应性的例子。
我们把单应性应用到棋盘格标定法中,第一步就是要求出从棋盘格角点的世界坐标到像素坐标的单应性变换矩阵H。求解步骤如下,注意这个是可以直接通过所拍摄的足够多照片求解的,这个很重要,很重要,很重要。
我们对公式稍微变形一下
由于世界坐标是我们自己定义的,为了计算方便,我们可以将棋盘格平面定义为Zw=0平面,定义第一个角点为原点,然后根据边长信息可以推导出所有的世界坐标,当然所有的坐标的Z=0,则公式变形为
其中a,s是缩放因子。
我们通过把矩阵H归一化,所以![]() ,H是一个3*3的矩阵,所以只剩下了8个未知元素。接下来开始求解H,s是个变量,这个也很重要,a是任意常量,也是缩放因子(个人理解,不知道正确不)。
,H是一个3*3的矩阵,所以只剩下了8个未知元素。接下来开始求解H,s是个变量,这个也很重要,a是任意常量,也是缩放因子(个人理解,不知道正确不)。
根据前面介绍的,我们已知世界坐标下的棋盘格角点,然后也通过计算,得到了对应的像素坐标。转换成数学语言就是
步骤如下
变形可以得到
借用一位博主的话,但是作为一个大学生,如果只会列公式,那么我们和咸鱼,,,嗯,我是说我们和小学生有什么区别。我们要列,矩,阵。唯有如此,才能体现出我们曾上过矩阵这门课,或者说,被它上过。我们把它写成矩阵的形式。
每一个点对应一个![]() ,由于每个Xw和Yw不一样,也反映了s是个变量
,由于每个Xw和Yw不一样,也反映了s是个变量
可以知道式子中所有的未知数只有H,只要最左边的矩阵的行数不小于8行,可知矩阵有解。可以看到一个对应点可以提供两条方程,一个棋盘格只能提供四个有效点,一个正方形的对角线延伸出去全部共线,所以一个棋盘格刚刚好可以提供4个有效点,也就是八条方程,所以矩阵可以求解。求解的方式有很多,例如SVD分解的方法。
标定过程
根据上述推导的,我们能够求解出H,且![]() ,但是H是内参数和外参数的具体表现,而我们要的是内参数,所以要分解H矩阵,得到内参数。
,但是H是内参数和外参数的具体表现,而我们要的是内参数,所以要分解H矩阵,得到内参数。
其中![]()
![]() 消失是因为
消失是因为![]() 。R是旋转矩阵,本身是一个正交阵,即R的转置等于R的逆。正交阵的每个列向量是两两正交且单位化的(即模为1),那么
。R是旋转矩阵,本身是一个正交阵,即R的转置等于R的逆。正交阵的每个列向量是两两正交且单位化的(即模为1),那么![]() 和
和![]() 是相互正交的。利用这些性质可以得到
是相互正交的。利用这些性质可以得到
将![]() 和
和![]() 带入上述公式,可得
带入上述公式,可得
发现两个约束条件都出现了,为了简化计算,令B=![]() 。
。
可以发现矩阵B是一个对称矩阵,那么他只有6个元素。两个约束条件有统一的表现形式![]() ,注意h是一个3*1的向量,具体写出来则是
,注意h是一个3*1的向量,具体写出来则是
展开为
写成矩阵的形式为
使用![]() 的定义(注意ij下标的关系),两个约束条件可以写成:
的定义(注意ij下标的关系),两个约束条件可以写成:
在这里V是已知的(可以根据H得到),并且每个场景对应一个v,但是b是纯内参数决定的,所以每个场景都不变化,所以只要有足够多的场景就可以求解出b。
至少要多少个场景?
假设有K的场景,每个场景只有四个有效点,每个场景对应6的外参数,相机有4个内参数(保持不变)。所以有解的前提是2*4*K>=6K+4.
乘以2是因为,每个点都是xy组成,一个点可以提供两个约束。
所以解得2K>=4,K>=2。
从另一个角度来将,B矩阵是由内参数矩阵M组成的,而M只含4个未知参数,所以一共只需要四条方程,而一个场景可以提供两个约束条件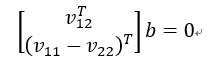 ,所以只要两个场景便可以求解。但是在现实中我们会追求鲁棒性,所以至少使用10幅7*8或者更大棋盘图像。
,所以只要两个场景便可以求解。但是在现实中我们会追求鲁棒性,所以至少使用10幅7*8或者更大棋盘图像。
我们将多个场景的约束条件写在一起Vb=0,则V是一个2K*6的矩阵,求解得到b。
得到b之后便可以求解内参数了。至于怎么从B到内参,我实在是搞不懂,只能直接套用结论了。大致上是又莫名其妙多了个缩放因子
结论
内参数
外参数
当我们在真实数据求解的时候,将向量r放置在一起的时候![]() 无法得到一个精确的旋转矩阵,即
无法得到一个精确的旋转矩阵,即![]() 不成立。
不成立。
要使式子成立,常用的技巧是使用SVD分解,SVD是将矩阵分解为一个对角阵D和两个正交阵U和V的数学方法。这允许我们将R转化为![]() .因为R本身是正交的,矩阵D必须是单位阵I,使得UI
.因为R本身是正交的,矩阵D必须是单位阵I,使得UI![]() 。我们可以通过对R的奇异分解,设置D为单位帧,用SVD方法再重新合成R,将R强制计算为吻合的旋转矩阵。(由于个人的数学水平实在有限,所以从结论到这里都是直接抄写learning opencv 的)。
。我们可以通过对R的奇异分解,设置D为单位帧,用SVD方法再重新合成R,将R强制计算为吻合的旋转矩阵。(由于个人的数学水平实在有限,所以从结论到这里都是直接抄写learning opencv 的)。
接下来求解畸变参数
到目前为止,我们一切的推导都没有考虑畸变参数。我们现在通过前面求解得到的相机内外参数,来解大的系统方程,得到畸变参数。
我们还是通过角点的匹配来得到方程组,具体如下
先把世界坐标转换到相机坐标
然后使用针孔模型,得到理论的像素坐标
然后通过一开始提出的畸变矫正公式,来拟合真实坐标![]() 和理论坐标
和理论坐标![]() 的关系。
的关系。
同样一个点可以提供两个方程,共有5个参数,所以至少需要3个点就可以求解,当然点更多一点,鲁棒性会更好。
到此,单目相机的内外参标定就介绍完了。
参考书籍:
learning opencv