Spiral Matrix 问题
看到一道题,很有意思。题面很简单,给一个矩阵,类似下面这样
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
要求旋转打印这个矩阵,结果是1 2 3 4 8 12 16 15 14 13 9 5 6 7 11 10这样。
这种问题很容易陷入怎么在局部转向的误区,更好的方法还是用逐步缩小问题规模的思路,每次解决一对左上右下坐标(lr,lc)(rr,rc)确定的一圈,一圈一圈往里走,直到把整个矩阵走完。对于每个边长L的圈,每次打印(L-1)长度转向,打印四次。
注意一下边界情况,两个坐标可能在一行或一列,这时候直接向右打印一行或向下打印一列就可以了。
public void SpiralMatrix(int[][] matrix) {
int lr = 0, lc = 0;
int rr = matrix.length-1, rc = matrix[0].length-1;
while(lr <= rr && lc <= rc) {
printFrame(matrix,lr,lc,rr,rc);
lr++;lc++;
rr--;lc--;
}
}
public void printFrame(int[][] matrix, int lr, int lc, int rr, int rc) {
if(lr == rr) {
for(int i = lc; i <= rc; i++) {
System.out.print(matrix[lr][i]+" ");
}
}else if(lc == rc) {
for(int i = lr; i <= rr; i++) {
System.out.print(matrix[i][lc]+" ");
}//左上右下在同一行/列,直接打印一行/列
}else{
int curR = lr;
int curC = lc;
while(curC != rc) {
System.out.print(matrix[curR][curC]+" ");//用两个指针代表现在的位置更易读
curC++;
}
while(curR != rr) {
System.out.print(matrix[curR][curC]+" ");
curR++;
}
while(curC != lc) {
System.out.print(matrix[curR][curC]+" ");
curC--;
}
while(curR != lr) {
System.out.print(matrix[curR][curC]+" ");
curR--;
}
}
}这道题核心的方法是一圈一圈解决问题,这样的思路可以推广到类似的问题。
给一个正方形矩阵,要求顺时针旋转90度输出,空间复杂度O(1)。
可以用上面的思路,一圈一圈向内逐渐完成旋转,对于每一圈,每次完成一组对应位置元素的旋转,只需要一个额外变量,空间复杂度O(1)。
public void spiralMatrix(int[][] m) {
int lr = 0, lc = 0;
int rr = m.length-1, rc = m[0].length-1;
while(lr < rr) {
spiralFrame(m, lr++, lc++, rr--, rc--);
}
}
public void spiralFrame(int[][]m, int lr, int lc, int rr, int rc) {
int tmp;
for(int i = 0; i < rr - lr; i++) {
tmp = m[lr][lc+i];
m[lr][lc+i] = m[rr-i][lc];
m[rr-i][rc] = m[rr][rc-i];
m[rr][rc-i] = m[lr+i][rc];
m[lr+i][lc] = tmp;
}
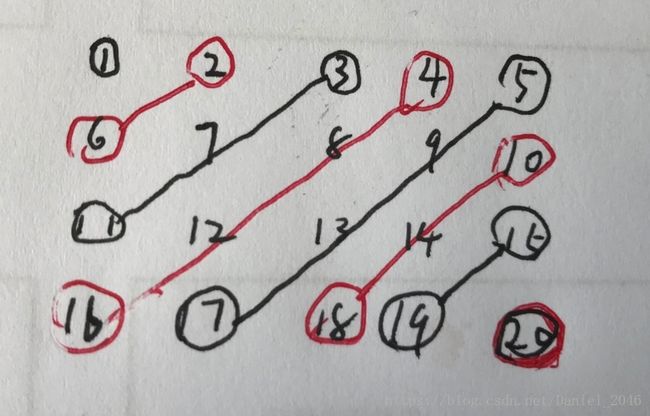
}还是给一个矩阵,这次正方形长方形都可以,要求按这样蛇形顺序打出来
(忽略字丑~)
先不管每条斜线上下移动的方向,这个矩阵可以看作是被一条一条斜线从左上到右下扫完的,每条斜线可以被两个端点确定,一条线的两个端点可能相等,像这样。
所以先设法用斜线扫完矩阵。观察一下上图,斜线可以用“右下端点”和“左上端点”确定,观察右下/左上端点的移动轨迹,一开始两端点都位于矩阵右上角,同时移动,右下端点先是向下,到底后向右;左上端点先是向右,到头后向下。最后两个端点在左下角再次重合。
用两组坐标表示斜线的两个端点,用一个boolean变量标识这次打印的上下方向,每次取反就可以了。
public void snakeMatrix(int[][] m) {
int lr = 0, lc = 0;
int rr = 0, rc = 0;
int endR = m.length-1, endC = m[0].length-1;
boolean downward = true;
while(lr <= endR) {
printLine(m, lr, lc, rr, rc, downward);
lr = (lc == endC)? lr+1: lr;
lc = (lc == endC)? lc: lc+1;
rr = (rr == endR)? rr: rr+1;
rc = (rr == endR)? rc+1: rc;
downward = !downward;
}
}
public void printLine(int[][] m, int lr, int lc, int rr, int rc, boolean downward) {
if(downward) {
while(lr <= rr) {
System.out.print(m[lr++][lc--]+" ");
}
}else {
System.out.print(m[rr--][rc++]+" ");
}
}