评测指标(metrics)

评测指标(metrics)

metric主要用来评测机器学习模型的好坏程度,不同的任务应该选择不同的评价指标, 分类,回归和排序问题应该选择不同的评价函数. 不同的问题应该不同对待,即使都是 分类问题也不应该唯评价函数论,不同问题不同分析.

回归(Regression)

1. 均方误差(MSE)

$$l(y,\hat{y})=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2\text{\hspace{1em}(1)}$$

2. 均方根误差(RMSE)

$$l(y,\hat{y})=\sqrt{\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2}\text{\hspace{1em}(2)}$$

3. 平均绝对误差(MAE)

$$l(y,\hat{y})=\frac{1}{n}\sum _{i=1}^n|y_i-{\hat{y}}_i|\text{\hspace{1em}(3)}$$

4. R Squared

$$R^2=1-\frac{({\sum }_{i=1}^n(y_i-\hat{y}i{)}^2)/n}{(\sum {i=1}^n(y_i-{\bar{y}}_i{)}^2)/n}\text{\hspace{1em}(4)}$$
其中: $\hat{y}$是预测值, $y$是真实值, $n$是样本个数, $\bar{y}$是$y$的平均值.

分类(Classification)

1. 准确率和错误率

$$acc(y,\hat{y})=\frac{1}{n}\sum _{i=1}^n{y}_i=\widehat{y_i}\text{\hspace{1em}(5)}$$
$$error(y,\hat{y})=1-acc(y,\hat{y})\text{\hspace{1em}(6)}$$

2. 混淆矩阵,精准率和召回率

对于二分类问题,可将样例根据其真是类别与学习器预测类别的组合划分为真正例(true positive, TP),假正例(false positive, FP),真反例(ture negative, TN),假反例(false negative, FN), 则有:TP+FP+TN+FN=样例总数. 分类结果的混淆矩阵(confusion matrix)如下:

则有精准率P和召回率R定义如下: $$P=\frac{TP}{TP+FP}\text{\hspace{1em}(7)}$$
$$R=\frac{TP}{TP+FN}\text{\hspace{1em}(8)}$$
则F1值定义如下: $$\frac{1}{F_1}=\frac{1}{2}\cdot (\frac{1}{P}+\frac{1}{R})\text{\hspace{1em}(9)}$$
$$F_1=\frac{2PR}{P+R}\text{\hspace{1em}(10)}$$

3. ROC和AUC

ROC全称是"受试者工作特征"(Receiver Operating Characteristic)曲线. 根据学习器的预测结果堆样例进行排序,按此顺序逐个把样本作为正例进行预测,每次计算出两个重要的值,分别以他们作为横纵坐标作图,就得到"ROC曲线". 其中ROC曲线的横轴是"假正例率"(False Positive Rate, FPR), 纵轴是"真正例率"(True Positive Rate, TPR), 注意这里不是上文提高的P和R. 其中:
$$TPR=\frac{TP}{TP+FN}\text{\hspace{1em}(11)}$$ $$FPR=\frac{FP}{TN+FP}\text{\hspace{1em}(12)}$$

现实使用中,一般使用有限个测试样例绘制ROC曲线,此时需要有有限个(真正例率,假正例率)坐标对. 绘图过程如下:

1. 给定$m^{+}$个正例和$m^{-}$个反例,根据学习器预测结果对样例进行排序,然后将分类阈值设为最大,此时真正例率和假正例率都为0,坐标在(0,0)处,标记一个点.
2. 将分类阈值依次设为每个样本的预测值,即依次将每个样本划分为正例.
3. 假设前一个坐标点是(x,y),若当前为真正例,则对应坐标为$(x,y+\frac{1}{m^{+}})$, 若是假正例,则对应坐标为$(x+\frac{1}{m^{-}},y)$
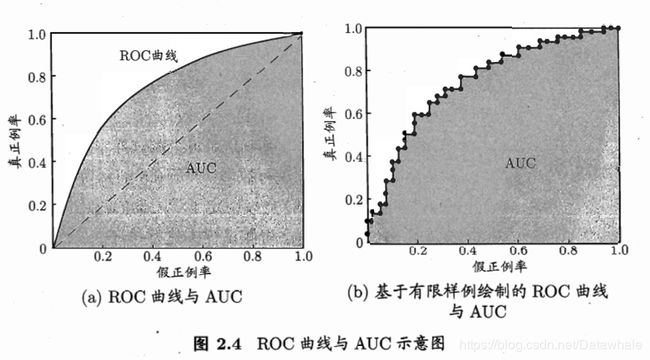
   线段连接相邻的点.

理想的图和现实的图对比如下图(其中对角线对应于"随机猜测"模型):

为了进行比较,较为合理的判别依据是ROC曲线下面的面积,即AUC(Area Under ROC Curve). 从上图看出,AUC可估算为:
$$AUC=\frac{1}{2}\sum _{i=1}^{m-1}(x_{i+1}-x_i)\cdot (y_i+y_{i+1})\text{\hspace{1em}(13)}$$
AUC考虑是样本排序的质量,因此它和排序误差有紧密联系.给定$m^{+}$个正例和$m^{-}$个负例,另$D^{+}$和$D^{-}$分别表示正和反例的集合,则排序损失定义为: $$l_{rank}=\frac{1}{m^{+}{m}^{-}}\sum _{x^{+}\in D^{+}}\sum _{x^{-}\in D^{-}}(I(f(x^{+})<f(x^{-}))+\frac{1}{2}I(f(x^{+})=f(x^{-})))\text{\hspace{1em}(14)}$$
即考虑每一对正反例,若正例的预测值小于反例,则记一个"罚分", 若相等,则记0.5个"罚分". 其实$l_{rank}$对应的是ROC曲线之上的面积,则有:
$$AUC=1-l_{rank}\text{\hspace{1em}(15)}$$

4. CTR和CVR

1. CTR
   CTR（Click-Through-Rate）即点击通过率,是互联网广告常用的术语,指网络广告（图片广告/文字广告/关键词广告/排名广告/视频广告等）的点击到达率,即该广告的实际点击次数（严格的来说,可以是到达目标页面的数量）除以广告的展现量(Show content). $$ctr=\frac{点击次数}{展示量}\text{\hspace{1em}(16)}$$
2. CVR
   CVR (Conversion Rate): 转化率。是一个衡量CPA广告效果的指标，简言之就是用户点击广告到成为一个有效激活或者注册甚至付费用户的转化率. $$cvr=\frac{点击量}{转化量}\text{\hspace{1em}(17)}$$

参考

1. 周志华 西瓜书
2. 李航 统计学习方法
3. https://baike.baidu.com/item/CVR/20215345
4. https://baike.baidu.com/item/CTR/10653699?fr=aladdin
5. https://www.cnblogs.com/shenxiaolin/p/9309749.html