康托展开

文字及图转自：http://www.cnblogs.com/1-2-3/archive/2011/04/25/generate-permutation-part2.html

代码转自：http://blog.csdn.net/synapse7/article/details/16901489

康托展开的公式是 X=an*(n-1)!+an-1*(n-2)!+…+ai*(i-1)!+…+a2*1!+a1*0! 其中，ai为当前未出现的元素中是排在第几个（从0开始）。
　　这个公式可能看着让人头大，最好举个例子来说明一下。例如，有一个数组 s = [“A”, “B”, “C”, “D”]，它的一个排列 s1 = [“D”, “B”, “A”, “C”]，现在要把 s1 映射成 X。n 指的是数组的长度，也就是4，所以
X(s1) = a4*3! + a3*2! + a2*1! + a1*0!
关键问题是 a4、a3、a2 和 a1 等于啥？
a4 = “D” 这个元素在子数组 [“D”, “B”, “A”, “C”] 中是第几大的元素。”A”是第0大的元素，”B”是第1大的元素，”C” 是第2大的元素，”D”是第3大的元素，所以 a4 = 3。
a3 = “B” 这个元素在子数组 [“B”, “A”, “C”] 中是第几大的元素。”A”是第0大的元素，”B”是第1大的元素，”C” 是第2大的元素，所以 a3 = 1。
a2 = “A” 这个元素在子数组 [“A”, “C”] 中是第几大的元素。”A”是第0大的元素，”C”是第1大的元素，所以 a2 = 0。
a1 = “C” 这个元素在子数组 [“C”] 中是第几大的元素。”C” 是第0大的元素，所以 a1 = 0。（因为子数组只有1个元素，所以a1总是为0）
所以，X(s1) = 3*3! + 1*2! + 0*1! + 0*0! = 20

#include  
const int fac[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320};///阶乘  

int KT(int s[], int n)  
{  
    int i, j, cnt, sum;  
    sum = 0;  
    for (i = 0; i < n; ++i)  
    {  
        cnt = 0;  
        for (j = i + 1; j < n; ++j)  
            if (s[j] < s[i]) ++cnt;  
        sum += cnt * fac[n - i - 1];  
    }  
    return sum;  
}  

int main()  
{  
    int a[] = {3, 5, 7, 4, 1, 2, 9, 6, 8};  
    printf("%d\n", 1 + KT(a, sizeof(a) / sizeof(*a))); ///1+98884  
}  

　如果已知 s = [“A”, “B”, “C”, “D”]，X(s1) = 20，能否推出 s1 = [“D”, “B”, “A”, “C”] 呢？
　　因为已知 X(s1) = a4*3! + a3*2! + a2*1! + a1*0! = 20，所以问题变成由 20 能否唯一地映射出一组 a4、a3、a2、a1？如果不考虑 ai 的取值范围，有
3*3! + 1*2! + 0*1! + 0*0! = 20
2*3! + 4*2! + 0*1! + 0*0! = 20
1*3! + 7*2! + 0*1! + 0*0! = 20
0*3! + 10*2! + 0*1! + 0*0! = 20
0*3! + 0*2! + 20*1! + 0*0! = 20
等等。但是满足 0 <= ai <= n-1 的只有第一组。可以使用辗转相除的方法得到 ai，如下图所示：

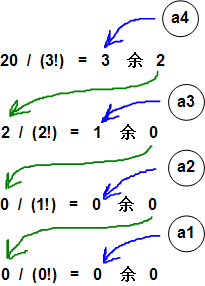
知道了a4、a3、a2、a1的值，就可以知道s1[0] 是子数组[“A”, “B”, “C”, “D”]中第3大的元素 “D”，s1[1] 是子数组 [“A”, “B”, “C”] 中第1大的元素”B”，s1[2] 是子数组 [“A”, “C”] 中第0大的元素”A”，s[3] 是子数组 [“C”] 中第0大的元素”C”，所以s1 = [“D”, “B”, “A”, “C”]。
这样我们就能写出一个函数 Permutation3()，它可以返回 s 的第 m 个排列。

#include  
#include  
const int fac[] = {1, 1, 2, 6, 24, 120, 720, 5040, 40320};///阶乘  

bool vis[10];  

///n为ans大小，k为全排列的编码  
void invKT(int ans[], int n, int k)  
{  
    int i, j, t;  
    memset(vis, 0, sizeof(vis));  
    --k;  
    for (i = 0; i < n; ++i)  
    {  
        t = k / fac[n - i - 1];  
        for (j = 1; j <= n; j++)  
            if (!vis[j])  
            {  
                if (t == 0) break;  
                --t;  
            }  
        ans[i] = j, vis[j] = true;  
        k %= fac[n - i - 1];///余数  
    }  
}  

int main()  
{  
    int a[10];  
    invKT(a, 5, 16);  
    for (int i = 0; i < 5; ++i)  
        printf("%d ", a[i]);///1 4 3 5 2  
}