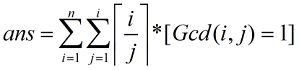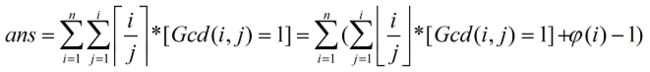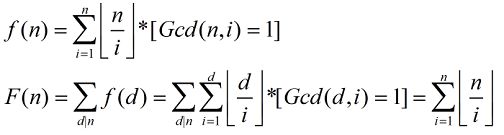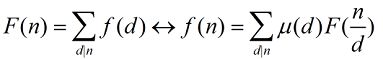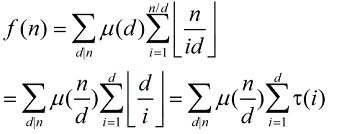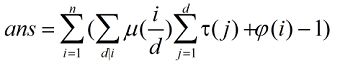hdu 6134(莫比乌斯反演)
Battlestation Operational
Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 464 Accepted Submission(s): 254
Problem Description
> The Death Star, known officially as the DS-1 Orbital Battle Station, also known as the Death Star I, the First Death Star, Project Stardust internally, and simply the Ultimate Weapon in early development stages, was a moon-sized, deep-space mobile battle station constructed by the Galactic Empire. Designed to fire a single planet-destroying superlaser powered by massive kyber crystals, it was the pet project of the Emperor, Darth Vader, and its eventual commander Grand Moff Wilhuff Tarkin to expound the military philosophy of the aptly named Tarkin Doctrine.
>
> — Wookieepedia
In the story of the Rogue One, the rebels risked their lives stolen the construction plan of the Death Star before it can cause catastrophic damage to the rebel base. According to the documents, the main weapon of the Death Star, the Superlaser, emits asymmetric energy in the battlefield that cause photons to annihilate and burns everything in a single shot.
You are assigned the task to estimate the damage of one shot of the Superlaser.
Assuming that the battlefield is an n×n grid. The energy field ignited by the Superlaser is asymmetric over the grid. For the cell at i-th row and j-th column, ⌈i/j⌉units of damage will be caused. Furthermore, due to the quantum effects, the energies in a cell cancel out if gcd(i,j)≠1 or i
The figure below illustrates the damage caused to each cell for n=100. A cell in black indicates that this cell will not be damaged due to the quantum effects. Otherwise, different colors denote different units of damages.
Your should calculate the total damage to the battlefield. Formally, you should compute
f(n)=∑i=1n∑j=1i⌈ij⌉[(i,j)=1],
where [(i,j)=1] evaluates to be 1 if gcd(i,j)=1, otherwise 0.
Input
There are multiple test cases.
Each line of the input, there is an integer n (1≤n≤106), as described in the problem.
There are up to 104 test cases.
Output
For each test case, output one integer in one line denoting the total damage of the Superlaser, f(n) mod 109+7.
Sample Input
1 2 3 10
Sample Output
1 3 8 110
Source
2017 Multi-University Training Contest - Team 8
Recommend
liuyiding | We have carefully selected several similar problems for you: 6160 6159 6158 6157 6156
参考文章:http://blog.csdn.net/brazy/article/details/77368202
题意:给出一个n*n的矩阵对于矩阵中每一个点(x, y) 如果x >= y && gcd(x, y) = 1, 那么这个点的值为 x / y 向上取整, 否则就为0,要求这个矩阵的各个点的值的总和。即如公式所见:。
对于这类问题需要多化解公式,直接从
分析:
首先设
因为gcd(i, j)等于1才有效,因此i / j 一定无法整除(除了j = 1),且结果就为 i / j + 1,因此有如下转化,其中φ(i)为欧拉函数
欧拉函数φ(n)定义为小于n中与n互质的个数。
然后就是重要发现:
然后运用莫比乌斯反演(反演过程挺精妙)
可得:
继续转化:
其中τ(n)表示n的约数个数,是积性函数也可以线性求出
做的时候只需要记录一个约数个数前缀和就可以了,答案也可以记录一个前缀和,然后就套上了欧拉函数和莫比乌斯板子了。(其实最重要的还是化解式子的思维,尤其是逆向思维)
代码:
#include
using namespace std;
typedef long long LL;
const int mod=1e9+7;
const int maxn=1e6+5;
bool vis[maxn];
LL ans[maxn];
int mu[maxn],prime[maxn],num[maxn];
int m[maxn],phi[maxn],p[maxn],pt;//m[i]是i的最小素因数,p是素数,pt是素数个数,phi[i]为i的欧拉函数的值
void make()
{
phi[1]=1;
int N=maxn;
int k;
for(int i=2;i