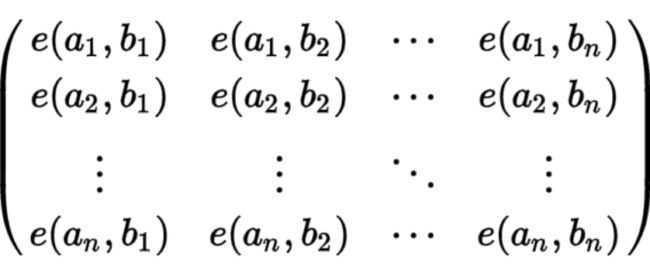牛客网多校1 Monotonic Matrix （L-G-V Lemma应用两侧，行列式）

题目：在所有的n*m的矩阵中，数出满足条件的矩阵的数量（% 1e9+7）
* Ai, j ∈ {0, 1, 2} for all 1 ≤ i ≤ n, 1 ≤ j ≤ m.
* Ai, j ≤ Ai + 1, j for all 1 ≤ i < n, 1 ≤ j ≤ m.
* Ai, j ≤ Ai, j + 1 for all 1 ≤ i ≤ n, 1 ≤ j < m.

考虑到01和12的分界线，所以就是求点(0,0)到点(n+1,m+1)的两条不相交（可重合）的路径/////因为可重合所以是(n+1,m+1)

Lindstrom-Gessel-Viennot Lemma

#include
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll c[2005][1005];
void init()
{
    c[0][0]=1;
    for(int i=1;i<=2000;i++)
    for(int j=0;j<=min(i,1000);j++)
    c[i][j]=(c[i-1][j]+(j>0?c[i-1][j-1]:0))%mod;
}
int n,m;
ll mp[3][3];
int main()
{
    init();
    while(~scanf("%d%d",&n,&m))
    {
        mp[1][1]=c[n+m][n];
        mp[1][2]=c[n+m][n-1];
        mp[2][1]=c[n+m][m-1];
        mp[2][2]=c[n+m][n];
        ll ans=(mp[1][1]*mp[2][2]%mod-mp[1][2]*mp[2][1]%mod+mod)%mod;
        printf("%lld\n",ans);
    }
    return 0;
}

对于一张无边权的DAG图，给定n个起点和对应的n个终点，这n条不相交路径的方案数为

det() （该矩阵的行列式）

其中e(a,b)为图上a到b的方案数

 

codeforces 348D

给定一张n*m带障碍的图，求从左上角到右下角不相交两条路径的方案

a1=(1,2) a2=(2,1) b1=(n-1,m) b2=(n,m-1) 应用该定理即可

mp={
    e(a1,b1)    e(a2,b2)
    e(a2,b1)    e(a2,b2)
    };

#include
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll path[3005][3005];
char s[3005][3005];
int n,m;
void solve(int x,int y)
{
    memset(path,0,sizeof path);
    if(s[x][y]=='.')//这里需要判断下。。。
    path[x][y]=1;
    for(int i=x;i<=n;i++)
    {
        for(int j=y;j<=m;j++)
        if(s[i][j]=='.')
        {
            if(i==x&&j==y)continue;
            path[i][j]=(path[i-1][j]+path[i][j-1])%mod;
        }
    }
}
ll mp[5][5];
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%s",s[i]+1);

    solve(1,2);
    mp[1][1]=path[n-1][m];//(1,2)-->(n-1,m)的路径数
    mp[1][2]=path[n][m-1];//(1,2)-->(n,m-1)的路径数

    solve(2,1);
    mp[2][1]=path[n-1][m];//(2,1)-->(n-1,m)的路径数
    mp[2][2]=path[n][m-1];//(2,1)-->(n,m-1)的路径数

    ll ans=(mp[1][1]*mp[2][2]%mod-mp[1][2]*mp[2][1]%mod+mod)%mod;///行列式求值
    printf("%lld\n",ans);
    return 0;
}

HDU 5852

有一个n*n个棋盘，现在要把m个棋子从第1行移到第n行，每步只能往下或往右，移动路径不能交叉，求路径的方案数。 
n≤100000,m≤100

#include
using namespace std;
typedef long long ll;
const int maxn=2e5;
const ll mod=1e9+7;
ll fac[maxn+10],inv[maxn+10];
ll qmod(ll x,ll p)
{
    ll ans=1;
    while(p)
    {
        if(p&1) (ans*=x)%=mod;
        p>>=1;
        (x*=x)%=mod;
    }
    return ans;
}
void init()
{
    fac[0]=1ll;
    for(int i=1;i<=maxn;i++)
        fac[i]=fac[i-1]*1ll*i%mod;
    inv[maxn]=qmod(fac[maxn],mod-2);
    for(int i=maxn-1;i>=0;i--)
        inv[i]=1ll*(i+1)*inv[i+1]%mod;
}
ll C(int n,int m)
{
    if(m>n) return 0;
    return fac[n]*inv[n-m]%mod*inv[m]%mod;
}
void debug(int n,ll a[][110])
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)printf("%lld ",a[i][j]);
        printf("\n");
    }
}
ll det(int N,ll a[][110])//求行列式det
{
    ll ans=1;
    int sign=0;
    for(int i=1;i<=N;i++)//当前行
    {
        for(int j=i+1;j<=N;j++)//当前之后的每一行，因为每一行的当前第一个数要转化成0（想想线性代数中行列式的计算）
        {
            int x=i,y=j;
            while(a[y][i])//利用gcd的方法，不停地进行辗转相除
            {
                ll t=a[x][i]/a[y][i];

                for(int k=i;k<=N;k++)
                    a[x][k]=(a[x][k]-a[y][k]*t)%mod;

                swap(x,y);
            }
            if(x!=i)//奇数次交换，则D=-D'整行交换
            {
                for(int k=1;k<=N;k++)
                    swap(a[i][k],a[x][k]);
                sign^=1;
            }
        }
        if(a[i][i]==0)//斜对角中有一个0，则结果为0
            return 0;
        else
            ans=ans*a[i][i]%mod;
    }
    if(sign!=0)
        ans*=-1;
    if(ans<0)
        ans+=mod;
    return ans;
}
ll e[110][110];
int t,n,m,a[110],b[110];
int main()
{
    scanf("%d",&t);
    init();
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(int i=1;i<=m;i++)
            scanf("%d",&a[i]);
        for(int i=1;i<=m;i++)
            scanf("%d",&b[i]);
        for(int i=1;i<=m;i++)
        for(int j=1;j<=m;j++)
            e[i][j]=C(n-1+b[j]-a[i],n-1);

        ll ans=det(m,e);
        printf("%lld\n",ans);
    }
    return 0;
}