hdu1150+poj3041 最小点覆盖or二分图最大匹配(匈牙利算法)

参考博客：https://blog.csdn.net/qq_40938077/article/details/80410356

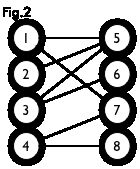
二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。准确地说：把一个图的顶点划分为两个不相交集   和  ，使得每一条边都分别连接 、   中的顶点。如果存在这样的划分，则此图为一个二分图。二分图的一个等价定义是：不含有「含奇数条边的环」的图。图 1 是一个二分图。为了清晰，我们以后都把它画成图 2 的形式。

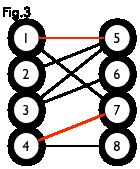
匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。例如，图 3、图 4 中红色的边就是图 2 的匹配

我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

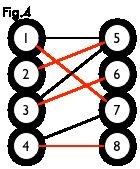
最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。图 4 是一个完美匹配。显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。但并非每个图都存在完美匹配。

上述是基本概念，接下来讲一下为匈牙利算法服务的一些概念

交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。

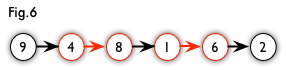
增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。例如，图 5 中的一条增广路如图 6 所示（图中的匹配点均用红色标出）：

增广路有一个重要特点：非匹配边比匹配边多一条。因此，研究增广路的意义是改进匹配。只要把增广路中的匹配边和非匹配边的身份交换即可。由于中间的匹配节点不存在其他相连的匹配边，所以这样做不会破坏匹配的性质。交换后，图中的匹配边数目比原来多了 1 条。其实，如果交替路以非匹配点结束的，那么这条交替路就是一条增广路

我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时，达到最大匹配（这是增广路定理）。匈牙利算法正是这么做的

接下来开始讲匈牙利算法

算法的基本思想：

基本思想：通过寻找增广路，把增广路中的匹配边和非匹配边的身份交换，这样就会多出一条匹配边，直到找不到增广路为止。

hdu1150

Machine Schedule

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 11134    Accepted Submission(s): 5529

 

Problem Description

As we all know, machine scheduling is a very classical problem in computer science and has been studied for a very long history. Scheduling problems differ widely in the nature of the constraints that must be satisfied and the type of schedule desired. Here we consider a 2-machine scheduling problem.

There are two machines A and B. Machine A has n kinds of working modes, which is called mode_0, mode_1, …, mode_n-1, likewise machine B has m kinds of working modes, mode_0, mode_1, … , mode_m-1. At the beginning they are both work at mode_0.

For k jobs given, each of them can be processed in either one of the two machines in particular mode. For example, job 0 can either be processed in machine A at mode_3 or in machine B at mode_4, job 1 can either be processed in machine A at mode_2 or in machine B at mode_4, and so on. Thus, for job i, the constraint can be represent as a triple (i, x, y), which means it can be processed either in machine A at mode_x, or in machine B at mode_y.

Obviously, to accomplish all the jobs, we need to change the machine's working mode from time to time, but unfortunately, the machine's working mode can only be changed by restarting it manually. By changing the sequence of the jobs and assigning each job to a suitable machine, please write a program to minimize the times of restarting machines.

 

 

Input

The input file for this program consists of several configurations. The first line of one configuration contains three positive integers: n, m (n, m < 100) and k (k < 1000). The following k lines give the constrains of the k jobs, each line is a triple: i, x, y.

The input will be terminated by a line containing a single zero.

 

 

Output

The output should be one integer per line, which means the minimal times of restarting machine.

 

 

Sample Input

5 5 10

0 1 1

1 1 2

2 1 3

3 1 4

4 2 1

5 2 2

6 2 3

7 2 4

8 3 3

9 4 3

0

 

 

Sample Output

3

题意：现在有A机器人和B机器人，现在有k个任务，每个任务都可以由A机器人或B机器人来完成，A机器人有n个任务模式，B机器人有m个模式，机器人在不同的模式中切换时都需要重启，现在A机器人和B机器人都处于0状态，

输入：第一行输入n，m，k如题意，接下来k行输入x，a，b，表示第x个任务可以由A机器人的a模式或者B机器人的B模式完成

当输入n为0时结束程序

输出：输出一个数，A机器人和B机器人最少的重启次数

思路：我们把A机器人的n种模式看成二分图左边的点，B机器人的m种模式看成二分图右边的点，每个任务看成连接二分图的边，我们的任务可以看成找出最少的点使得这些点连接所有的边，这就是最小点覆盖

最小点覆盖=最大匹配。。。。。。自己去看证明

所以我们只需要求出二分图的最大匹配就好了

AC代码：

#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define LL long long
const int MOD=1e9+7;
const int inf=0x3f3f3f3f;
const LL inff=0x3f3f3f3f3f3f3f3f;
const LL MAX_N=10005;
const LL MAX_M=50005;
#define MEF(x) memset(x,-1,sizeof(x))
#define ME0(x) memset(x,0,sizeof(x))
#define MEI(x) memset(x,inf,sizeof(x))
int mapt[105][105];
int cl[105];
int vis[105];
int n,m,k;
int point(int x)
{
    for(int m1=1;m1<=m;m1++)
    {
        if(!vis[m1]&&mapt[x][m1])
        {
            vis[m1]=1;
            if(cl[m1]==-1||point(cl[m1]))//递归，算法关键
            {
                cl[m1]=x;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    while(cin>>n&&n)
    {
        cin>>m>>k;
        int x,a,b;
        ME0(mapt);
        MEF(cl);
        ME0(vis);
        for(int k1=1;k1<=k;k1++)
        {
            cin>>x>>a>>b;
            mapt[a][b]=1;
        }
        int ans=0;
        for(int n1=1;n1<=n;n1++)
        {
            ME0(vis);
            ans+=point(n1);
        }
        cout<

poj3041

Asteroids

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 27458		Accepted: 14744

Description

Bessie wants to navigate her spaceship through a dangerous asteroid field in the shape of an N x N grid (1 <= N <= 500). The grid contains K asteroids (1 <= K <= 10,000), which are conveniently located at the lattice points of the grid.

Fortunately, Bessie has a powerful weapon that can vaporize all the asteroids in any given row or column of the grid with a single shot.This weapon is quite expensive, so she wishes to use it sparingly.Given the location of all the asteroids in the field, find the minimum number of shots Bessie needs to fire to eliminate all of the asteroids.

Input

* Line 1: Two integers N and K, separated by a single space.
* Lines 2..K+1: Each line contains two space-separated integers R and C (1 <= R, C <= N) denoting the row and column coordinates of an asteroid, respectively.

Output

* Line 1: The integer representing the minimum number of times Bessie must shoot.

Sample Input

3 4
1 1
1 3
2 2
3 2

Sample Output

2

Hint

INPUT DETAILS:
The following diagram represents the data, where "X" is an asteroid and "." is empty space:
X.X
.X.
.X.

OUTPUT DETAILS:
Bessie may fire across row 1 to destroy the asteroids at (1,1) and (1,3), and then she may fire down column 2 to destroy the asteroids at (2,2) and (3,2).

题意：有一个N*N的网格,该网格有K个障碍物.你有一把武器,每次你使用武器可以清楚该网格特定行或列的所有障碍.问你最少需要使用多少次武器能清除网格的所有障碍物?

输入：第一行两个数N，K如题意，接下来K行每行两个数a，b表示a行b列有障碍物，

输出：使用武器的最少的次数

思路：把N*N的表格看成左边N个点右边N个点的二分图，障碍物看成连接二分图的边，和上一题一样需要求最小点覆盖，即求最大匹配

AC代码：

#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define LL long long
const int MOD=1e9+7;
const int inf=0x3f3f3f3f;
const LL inff=0x3f3f3f3f3f3f3f3f;
const LL MAX_N=10005;
const LL MAX_M=50005;
#define MEF(x) memset(x,-1,sizeof(x))
#define ME0(x) memset(x,0,sizeof(x))
#define MEI(x) memset(x,inf,sizeof(x))
int n,k;
int mapt[505][505];
int vis[505];
int cl[505];
int point(int x)
{
    for(int n2=1;n2<=n;n2++)
    {
        if(!vis[n2]&&mapt[x][n2])
        {
            vis[n2]=1;
            if(cl[n2]==-1||point(cl[n2]))
            {
                cl[n2]=x;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    cin>>n>>k;
    ME0(mapt);
    MEF(cl);
    for(int k1=1;k1<=k;k1++)
    {
        int a,b;
        cin>>a>>b;
        mapt[a][b]=1;
    }
    int ans=0;
    for(int n1=1;n1<=n;n1++)
    {
        ME0(vis);
        ans+=point(n1);
    }
    cout<