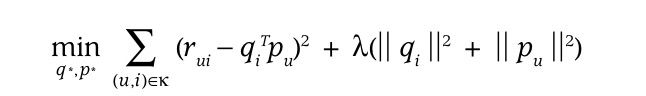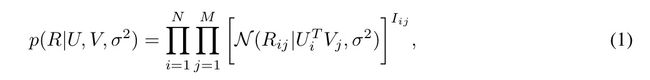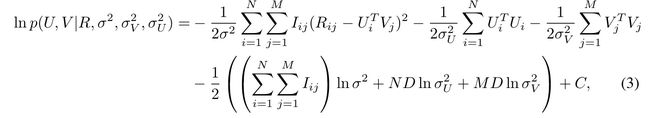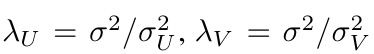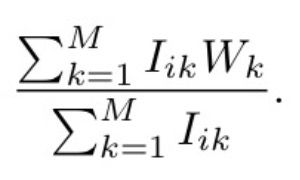MF的主要思想其实就是假设,我们有N个用户,M个items,我们正常会有一个M*N的评分矩阵,然而这个矩阵可能很稀疏,或者关联性很强,那么我们试图通过降维来达到一个更好的效果,降维的方法就是抽象出M个items的F个特征,这个所谓特征就叫latent feature,比如我们现在有M个电影,但是M太大,我们觉得没必要对于所有的电影进行一个个分析,我们宁愿把M看成多个标签组成的电影,比如电影《复仇者联盟》,我们不把它单独看成一个电影,而是看成多个标签的组合,如“科幻”,“漫画”,“超级英雄”等这几个标签。同时,我们把N个用户对于电影的评分转化为对这些标签的接受程度,如用户A特别喜欢看科幻类电影,那么他对于这一类标签的评分就很高,同时他特别讨厌言情,那么他对这一类标签的评分甚至可能为负值,那么对他来说,《复仇者联盟》这部电影可能就非常适合他,因为《复仇者联盟》的科幻类标签评分很高,而言情几乎没有。
通过这样的转化,好处是显而易见的。首先我们存储的空间大大减小,M的值可能大到几百万,但是标签的数量可能只有几百。其次我们对于那些给出评分非常少的用户也能有比较好的预测,试想一下,有几百万个不同电影,那么只有几个电影评分的用户,你是很难直接找到他对其他电影的评分的。但是,由于我们的F很小,可能只要几个评分,非常少的样本也能拟合不错的数据,我们可以探测到他对某些标签的喜爱,再把这些标签得分较高的电影推荐给他。
那么显然我们现在需要得到一个训练的损失函数,在MF里,这个函数是
这里的r就是原始的评分矩阵,qi指的是items的各项指标的评分,pu是用户对于各项指标的评分,后面的项是为了防止过拟合情况出现。
接下来是PMF,PMF引入了概率模型,首先假设,用户的评分相对于latent feature是满足高斯分布的,也就是说,如果我们已经掌握了items相对于标签的得分V和user相对于标签的评分U,那么用户的评分将会有很大的几率偏离这个预测值不远(高斯分布的特性)
同样的,对于各个标签的得分,我们也认为他满足高斯分布,不过这一次,他的均值应该为0,为什么为0呢?因为有可能喜欢有可能不喜欢,因此有正有负,那么为0应该是最可能的情况。
有了这三个假设的高斯分布,我们就可以使用贝叶斯推导了,我们关心的是在给定的三个方差参数和评分下,U和V分别会是多少,因为有了U和V,我们就能去预测之后的用户的评分了。
所以我们写出如下面公式的概率
然后我们的目的当然是使它尽可能的大,于是我们用它log函数来求最大值
这个函数是不是跟之前MF的函数非常像?仔细观察发现,其实不就是系数换了一个写法嘛...
其实MF的优化目标函数就是PMF的优化目标函数在
的情况下的一个特例而已。从这个角度上来讲,PMF似乎更加接近本质一些,从PMF的角度上来理解这个问题,我们对于过拟合情况的容忍程度(也就是lamda),其实无非就是我们对于原来的那个假设高斯分布的方差的选择而已。如果我们非常不希望过拟合情况出现,也就是说lamda非常大,那么用户和items对于标签的评分的变化程度相对于评分的变化程度就非常的小。这就是说,我们不希望通过选择一些非常“奇特”,变化特别大的latent feature
的系数,去保证我们的预测值跟原来的评分r保持一值。
同时,如果我们觉得现有的拟合情况并不理想,我们可以通过改变PMF的假设高斯分布的系数来得到更好的拟合状态。
比如constrained PMF
它的思想主要是基于,现在我们认为默认情况下用户对于标签的评分满足高斯分布,那么对于那些只给出很少评分的人,他们的评分很难对于整体的概率产生很大的影响,因此我们在拟合U和V的时候,把他们的影响忽略掉了,从而得出了一个跟“去掉他们也没什么不同”的U和V,这样从U和V的整体预测角度来说是没什么不对,但是对于这一个用户的预测就有了很大的区别,在这种时候,我们仅仅用U和V去预测这一个用户,会得到与平均值非常接近的评分。但是这显然不是我们想要的结果。因此我们引入了一个新的指标矩阵W
从而有了这样一个新的预测函数,这个函数应该要满足的需求是,他对于我们原来的整体参数不能有太大的修改,也就是对于评分很多的用户,不能有太大偏差,但是对于评分非常少的用户,我们希望能够有很大的不同。这个不同,就是基于用户已经有的评分,假设用户已经给这个电影进行了评分,那么这个电影的所有标签的评分都应该被纳入到考虑当中来了。也可以认为,我们假设U的高斯分布,它的均值已经不为0了,它的均值应该为已经被用户评分过的电影的标签的分数的平均。
而Yi可以看做是一个偏差的随机变量,这样写只是为了方便,也可以把Ui写成满足均值为
而方差为原来的sigma(U)的一个高斯分布。本质上只是对于假设Ui所满足的高斯分布的一个变换而已。
我们可以从概率论的角度上来论证这样为何对于高评分和低评分用户的影响不同。实际上,可以把这个UI满足的新的均值看做一个随机变量P,假设用户I评分了k个电影,那么P的值是k个均值为0的高斯随机变量之和除以k,那么由概率论的知识,P的方差应该为W的方差的k分之一,也就是说,随着k增大,p的变化程度越来越小,越来越稳定在均值0的附近,于是Ui就跟Yi差不多了。也就是说,高评分用户在新的体系下,他们的评分预测与无约束PMF的预测变化不大。