动态规划(Dynamic Programming)
本文包括:
- 动态规划定义
- 状态转移方程
- 动态规划算法步骤
- 最长非降子序列(LIS)
- 最大乘积子串
- Unique Paths
- Unique Paths II
- Minimum Path Sum
- Triangle
- 最长公共自序列(LCS)
- 编辑距离
- 交替字符串
- 矩阵链乘积
前文引自:http://www.hawstein.com/posts/dp-novice-to-advanced.html
1、 什么是动态规划,我们要如何描述它?
动态规划算法通常基于一个递推公式及一个或多个初始状态。 当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度, 因此它比回溯法、暴力法等要快许多。
首先,我们要找到某个状态的最优解,然后在它的帮助下,找到下一个状态的最优解。
2、“状态”代表什么及如何找到它?
“状态”用来描述该问题的子问题的解。原文中有两段作者阐述得不太清楚,跳过直接上例子。
如果我们有面值为1元、3元和5元的硬币若干枚,如何用最少的硬币凑够11元? (表面上这道题可以用贪心算法,但贪心算法无法保证可以求出解,比如1元换成2元的时候)
首先我们思考一个问题,如何用最少的硬币凑够i元(i<11)?为什么要这么问呢? 两个原因:1.当我们遇到一个大问题时,总是习惯把问题的规模变小,这样便于分析讨论。 2.这个规模变小后的问题和原来的问题是同质的,除了规模变小,其它的都是一样的, 本质上它还是同一个问题(规模变小后的问题其实是原问题的子问题)。
好了,让我们从最小的i开始吧。当i=0,即我们需要多少个硬币来凑够0元。 由于1,3,5都大于0,即没有比0小的币值,因此凑够0元我们最少需要0个硬币。 (这个分析很傻是不是?别着急,这个思路有利于我们理清动态规划究竟在做些什么。) 这时候我们发现用一个标记来表示这句“凑够0元我们最少需要0个硬币。”会比较方便, 如果一直用纯文字来表述,不出一会儿你就会觉得很绕了。
那么, 我们用d(i)=j来表示凑够i元最少需要j个硬币。于是我们已经得到了d(0)=0, 表示凑够0元最小需要0个硬币。当i=1时,只有面值为1元的硬币可用, 因此我们拿起一个面值为1的硬币,接下来只需要凑够0元即可,而这个是已经知道答案的, 即d(0)=0。所以,d(1)=d(1-1)+1=d(0)+1=0+1=1。当i=2时, 仍然只有面值为1的硬币可用,于是我拿起一个面值为1的硬币, 接下来我只需要再凑够2-1=1元即可(记得要用最小的硬币数量),而这个答案也已经知道了。 所以d(2)=d(2-1)+1=d(1)+1=1+1=2。
一直到这里,你都可能会觉得,好无聊, 感觉像做小学生的题目似的。因为我们一直都只能操作面值为1的硬币!耐心点, 让我们看看i=3时的情况。当i=3时,我们能用的硬币就有两种了:1元的和3元的( 5元的仍然没用,因为你需要凑的数目是3元!5元太多了亲)。 既然能用的硬币有两种,我就有两种方案。如果我拿了一个1元的硬币,我的目标就变为了: 凑够3-1=2元需要的最少硬币数量。即d(3)=d(3-1)+1=d(2)+1=2+1=3。 这个方案说的是,我拿3个1元的硬币;第二种方案是我拿起一个3元的硬币, 我的目标就变成:凑够3-3=0元需要的最少硬币数量。即d(3)=d(3-3)+1=d(0)+1=0+1=1. 这个方案说的是,我拿1个3元的硬币。
好了,这两种方案哪种更优呢? 记得我们可是要用最少的硬币数量来凑够3元的。所以, 选择d(3)=1,怎么来的呢?具体是这样得到的:d(3)=min{d(3-1)+1, d(3-3)+1}。
从以上的文字中, 我们要抽出动态规划里非常重要的两个概念:状态和状态转移方程。
上文中d(i)表示凑够i元需要的最少硬币数量,我们将它定义为该问题的”状态”, 这个状态是怎么找出来的呢?我在另一篇文章 动态规划之背包问题(一)中写过: 根据子问题定义状态。你找到子问题,状态也就浮出水面了。 最终我们要求解的问题,可以用这个状态来表示:d(11),即凑够11元最少需要多少个硬币。
-
那状态转移方程是什么呢?既然我们用d(i)表示状态,那么状态转移方程自然包含d(i), 上文中包含状态d(i)的方程是:d(3)=min{d(3-1)+1, d(3-3)+1}。没错, 它就是状态转移方程,描述状态之间是如何转移的。当然,我们要对它抽象一下,
d(i)=min{ d(i-vj)+1 },其中i-vj >=0,vj表示第j个硬币的面值; -
伪代码:
依次计算,可以计算出11元至少要3枚硬币。
3、DP 算法步骤
动态规划算法一般用来求解最优化问题,当问题有很多可行解,而题目要求寻找这些解当中的“最大值”/“最小值”时,通常可以采用DP。
动态规划算法与分治法相似,都是通过组合子问题的解来求解原问题。所不同的是,动态规划应用于子问题重叠的情况,在递归求解子问题的时候,一些子子问题可能是相同的,这种情况下,分治法会反复地计算同样的子问题,而动态规划对于相同的子问题只计算一次。
-
动态规划算法的设计步骤:
1、刻画最优解的结构特征(寻找最优子结构) 2、递归地定义最优解的值(确定递归公式,动态规划法的重点就是这个) 3、计算最优解的值(有两种方法:带备忘录自顶向下法、自底向上法) 4、利用计算出的信息构造一个最优解(通常是将具体的最优解输出)
最优子结构:问题的最优解包含的子问题的解相对于子问题而言也是最优的。
并非所有组合优化问题都具有最优子结构特性。
4、最长非降子序列(LIS)
-
问题描述:
一个序列有N个数:A[1],A[2],…,A[N],求出最长非降子序列的长度。
(讲DP基本都会讲到的一个问题LIS:longest increasing subsequence) -
思路:
假如我们考虑求A[1],A[2],…,A[i]的最长非降子序列的长度,其中i
然后我们定义d(i),表示前i个数中以A[i]结尾的最长非降子序列的长度。
如果我们把d(1)到d(N)都计算出来,那么最终我们要找的答案就是这里面最大的那个。
OK,状态找到了,下一步找出状态转移方程。
-
可以举个例子,然后求出前面几项,找出递推规律
d(i)可以用下面的状态转移方程得到:
d(i) = max{1, d(j)+1},其中j -
Python 代码:
def LIS(A): d = [0 for i in range(len(A))] for i in range(len(A)): d[i] = 1 # 就算前面所有元素都比当前大,那么至少可以包含自身,所以长度默认值为1 for j in range(i): if A[i] >= A[j] and d[j]+1 > d[i]: d[i] = d[j] + 1 return max(d) A = [5, 3, 4, 8, 6, 7] print(LIS(A))
另一个解法:利用LCS思想(第9点)
构造一个新序列,B,它是对A进行降序排列而得。
此时求最长非增子序列,调用LCS-LENGTH即可求出A与B的最长公共子序列,这个序列就是最后的解。
5、最大乘积子串
-
题目描述:
给一个浮点数序列,取最大乘积连续子串的值,例如 -2.5,4,0,3,0.5,8,-1,则取出的最大乘积连续子串为3,0.5,8。
也就是说,上述数组中,3 0.5 8这3个数的乘积30.58=12是最大的,而且是连续的。 -
思路:
因为有正有负,下次要处理的 a[i] 可能是负,所以每次都要存储最小的子串乘积值,负负得正,得出的结果有可能还更大。
-
递推方程:
maxend = max(max(maxend * a[i], minend * a[i]), a[i]); minend = min(min(maxend * a[i], minend * a[i]), a[i]); -
Python 代码:
def maxProductSubstring(a): maxend, minend, maxresult = a[0], a[0], a[0] for i in range(1,len(A)): maxend = max(max(maxend * a[i], minend * a[i]), a[i]) minend = min(min(maxend * a[i], minend * a[i]), a[i]) maxresult = max(maxend, maxresult) return maxresult A = [-2.5, 4, 0, 3, 0.5, 8, -1] print(maxProductSubstring(A))
6、Unique Paths
-
Leetcode:62. Unique Paths
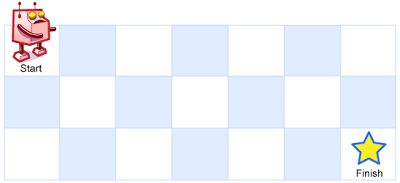
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
-
Solution:
class Solution(object): def uniquePaths(self, m, n): """ :type m: int :type n: int :rtype: int """ c = [[0 for i in range(n+1)] for i in range(m+1)] for i in range(n+1): c[0][i] = 0 for i in range(m+1): c[i][0] = 0 for i in range(1, m+1): for j in range(1, n+1): if i == 1 and j == 1: c[i][j] = 1 else: c[i][j] = c[i-1][j] + c[i][j-1] return c[i][j] sol = Solution() print(sol.uniquePaths(1, 1))
7、Unique Paths II
-
Leetcode:63. Unique Paths II
Follow up for "Unique Paths":
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and empty space is marked as 1 and 0 respectively in the grid.
For example,
There is one obstacle in the middle of a 3x3 grid as illustrated below.[
[0,0,0],
[0,1,0],
[0,0,0]
]The total number of unique paths is 2.
Note: m and n will be at most 100.
-
solution:
class Solution(object): def uniquePathsWithObstacles(self, obstacleGrid): """ :type obstacleGrid: List[List[int]] :rtype: int """ m = len(obstacleGrid) n = len(obstacleGrid[0]) dp = [[0 for i in range(n+1)] for i in range(m+1)] dp[1][1] = 1 for i in range(1, m+1): for j in range(1, n+1): if obstacleGrid[i-1][j-1] == 1: dp[i][j] = 0 elif i == 1 and j == 1: dp[1][1] = 1 else: dp[i][j] = dp[i-1][j] + dp[i][j-1] return dp[m][n] sol = Solution obstacleGrid = [ [0, 0, 0], [0, 1, 0], [0, 0, 0] ] print(sol.uniquePathsWithObstacles(sol, obstacleGrid))
8、Minimum Path Sum
-
Leetcode:64. Minimum Path Sum
Given a m x n grid filled with non-negative numbers,
find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
-
solution:
class Solution(object): def minPathSum(self, grid): """ :type grid: List[List[int]] :rtype: int """ m = len(grid) if m > 0 and len(grid[0]) > 0: n = len(grid[0]) else: return 0 dp = [[0 for i in range(n+1)] for i in range(m+1)] for i in range(m+1): dp[i][0] = float('inf') for i in range(n+1): dp[0][i] = float('inf') dp[1][1] = grid[0][0] for i in range(1, m+1): for j in range(1, n+1): if i == 1 and j == 1: dp[i][j] = grid[i-1][j-1] elif dp[i-1][j] < dp[i][j-1]: dp[i][j] = dp[i-1][j] + grid[i-1][j-1] else: dp[i][j] = dp[i][j-1] + grid[i-1][j-1] return dp[m][n]
9、Triangle
-
Leetcode:120. Triangle
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[ [2], [3,4], [6,5,7], [4,1,8,3] ]The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle. -
第一次尝试:
class Solution(object): def minimumTotal(self, triangle): """ :type triangle: List[List[int]] :rtype: int """ length = len(triangle) minSum = triangle[0][0] index = 0 for i in range(1, length): if triangle[i][index] < triangle[i][index+1]: minSum += triangle[i][index] else: minSum += triangle[i][index+1] index += 1 return minSum解释:
有点类似于贪心,每一步都寻找最优的,但是却没想到,全局最优可能是另外一种情况,比如下面的测试用例:Submission Result: Wrong Answer More Details Input: [[-1],[2,3],[1,-1,-3]] Output: 0 Expected: -1很明显,按照我的程序,走法是:-1 2 -1 = 0。
但是其实最优解是 -1 3 -3 = -1。 -
需要辅助空间 O(n^2) 的 DP 解法:
''' extra space: O(n^2) using 'top to bottom' thought ''' def minimumTotal(self, triangle): """ :type triangle: List[List[int]] :rtype: int """ length = len(triangle) dp = [[0 for i in range(j+1)] for j in range(length)] # dp[i][j] means element of row i column j is the last one of the min_path dp[0][0] = triangle[0][0] for i in range(1, length): for j in range(i+1): if j == 0: dp[i][j] = dp[i-1][j] + triangle[i][j] elif j == i: dp[i][j] = dp[i-1][j-1] + triangle[i][j] elif dp[i-1][j] < dp[i-1][j-1]: dp[i][j] = dp[i-1][j] + triangle[i][j] else: dp[i][j] = dp[i-1][j-1] + triangle[i][j] return min(dp[length-1])理解不难,同样是构建二维数组,dp[i][j] 的意思是以 triangle[i][j] 结尾的最小路径和。这其实就是带备忘录的自顶向下办法。
-
需要辅助空间 O(n) 的 DP 解法(推荐!):
''' extra space: O(n) using 'bottom to top' thought ''' def minimumTotal_bottomtotop(self, triangle): """ :type triangle: List[List[int]] :rtype: int """ length = len(triangle) dp = triangle[length-1] for i in range(length-2, -1, -1): for j in range(i+1): dp[j] = min(dp[j], dp[j+1]) + triangle[i][j] return dp[0]这种办法是从底往上,dp 只是一维数组,在每层操作时,仅记录该层的各元素结尾的最小路径和,并且路径是从底往上。在处理不同层时,dp 根据下一层的计算结果算出当前层的值,所以一直在变。辅助空间只有 O(n)。
10、最长公共子序列(LCS)
最长公共子序列(Longest Common Subsequence)是一个在一个序列集合中(通常为两个序列)用来查找所有序列中最长子序列的问题。这与查找最长公共子串的问题不同的地方是:子序列不需要在原序列中占用连续的位置 。最长公共子序列问题是一个经典的计算机科学问题,也是数据比较程序,比如Diff工具,和生物信息学应用的基础。它也被广泛地应用在版本控制,比如Git用来调和文件之间的改变。
-
LCS 问题可以用动态规划思想完美解决:
设二维数组 f[i][j] 表示:数组 X 的前 i 位与数组 Y 的前 j 位的最长公共子序列的长度
-
则有:
f[i][j] = same(1,1) f[i][j] = max{f[i-1][j-1] + same(i,j), f[i-1][j], f[i][j-1]} 其中,same(a,b) 表示:当 X 的第 a 位与 Y的第 b 位完全相同时为“1”,否则为“0”。
-
综上,可以总结出如下的算法,用B[i,j]来作标记,
用"↖"表示序列 X 和 Y 的当前最后两项 x[i] 和 y[j] 相等; 用“↑”表示选择时不考虑 x[i],即 f[i][j] = f[i-1][j]; 用“←”表示选择时不考虑 y[j],即 f[i][j] = f[i][j-1] LCS_LENGTH(X, Y): for i := 1 to m C[i,0] := 0 for j := 1 to n C[0,j] := 0 for i := 1 to m for j := 1 to n if X[i] = Y[j] C[i,j] := C[i-1,j-1] + 1 B[i,j] := "↖" else if C[i-1,j] >= C[i, j-1] C[i,j] := C[i-1,j] B[i,j] := "↑" else C[i,j] := C[i,j-1] B[i,j] : "←" -
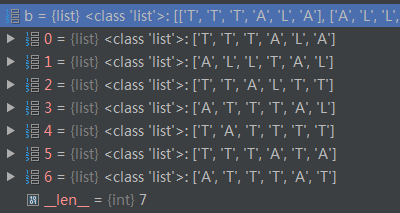
为了更加直观,这里用图表形象给出:
-
Python 代码(A表示↖,T表示↑,L表示←):
def LCS_LENGTH(X, Y): m = len(X) n = len(Y) c = [[0 for i in range(n+1)] for i in range(m+1)] b = [[0 for i in range(n)] for i in range(m)] for i in range(1, m + 1): for j in range(1, n + 1): if X[i-1] == Y[j-1]: c[i][j] = c[i-1][j-1] + 1 b[i-1][j-1] = "A" elif c[i-1][j] >= c[i][j-1]: c[i][j] = c[i-1][j] b[i-1][j-1] = "T" else: c[i][j] = c[i][j-1] b[i-1][j-1] = "L" return c, b def print_lcs(b, X, i, j): if i == -1 or j == -1: return if b[i][j] == "A": print_lcs(b, X, i-1, j-1) print(X[i]) elif b[i][j] == "T": print_lcs(b, X, i-1, j) else: print_lcs(b, X, i, j-1) return Y = "BDCABA" X = "ABCBDAB" c, b = LCS_LENGTH(X, Y) print_lcs(b, X, len(X)-1, len(Y)-1) -
代码细节:
-
创建二维数组,并且不会出现引用的问题(引用问题是一改就改了多处)
c = [[0 for i in range(n+1)] for i in range(m+1)] -
b 是辅助的一个二维数组(表),用来指示当前的路径选择(走对角A,还是走上T,还是走左L),实际上,《算法导论》中也明确指出这里可以省略,进而在 print_lcs 过程中做比较,这样可以节省辅助空间,但是这样比较浅显易懂
-
构造完表后,就可以调用 print_lcs 过程来得到路径了,在过程中使用了递归的思想,并且最后输出的顺序是从字符串的左边到右边的
"C:\Program Files\Python36\python.exe" D:/PythonProject/DataStructure-Algorithm/DynamicProgramming/LCS.py B C B A Process finished with exit code 0
-
11、编辑距离
-
题目描述:
给定一个源串和目标串,能够对源串进行如下操作:
- 在给定位置上插入一个字符
- 替换任意字符
- 删除任意字符
写一个程序,返回最小操作数,使得对源串进行这些操作后等于目标串,源串和目标串的长度都小于2000。
-
思路:
动态规划,构建二维数组,注意二维数组的第0行和第0列不是全0的。
可以想象,如果source 为空,想要转换为 target,则肯定要执行 len(target) = n 次操作,所以dp[i][j]赋初值时要注意这点。
-
递推方程:
//dp[i,j]表示表示源串S[0…i] 和目标串T[0…j] 的最短编辑距离 dp[i,j] = min {dp[i-1,j]+1, dp[i,j-1]+1, dp[i-1,j-1] + (s[i] == t[j] ? 0 : 1) } //分别表示:删除1个,添加1个,替换1个(相同就不用替换)。 -
解释:
插入是A在和B的前j-1个比,然后再在A的基础上进行插入一个字符,插入的字符是B的第j位,所以插入的代价是dp[i][j-1]+1
删除是A的前i-1个和B的j个比,因为把A删除了一个字符,所以删除的代价是dp[i-1][j]+1
替换是A的前i-1个和B的j-1个比,然后把A的第i位变成B的第j位。所以编辑的代价是dp[i-1][j-1]+1
-
python 代码:
def editDistance(source, target): m = len(source) n = len(target) dp = [[0 for i in range(n+1)] for i in range(m+1)] for i in range(n+1): dp[0][i] = i for i in range(m+1): dp[i][0] = i for i in range(1, m+1): for j in range(1, n+1): if source[i-1] == target[j-1]: dp[i][j] = dp[i-1][j-1] else: dp[i][j] = min(min(dp[i][j-1], dp[i-1][j]), dp[i-1][j-1]) + 1 return dp[m][n] source = "abc" target = "axxxbxxxc" print(editDistance(source, target))
12、交替字符串
Leetcode: 97. Interleaving String
-
题目描述:
输入三个字符串s1、s2和s3,判断第三个字符串s3是否由前两个字符串s1和s2交错而成,即不改变s1和s2中各个字符原有的相对顺序,
例如当s1 = “aabcc”,s2 = “dbbca”,s3 = “aadbbcbcac”时,则输出true,但如果s3=“accabdbbca”,则输出false。
-
思路:
多个字符串做“比较”的问题,大多都可以用DP求解。
构建二维数组,一般其规模为:(m+1)*(n+1)。
令dp[i][j]代表s3[0...i+j-1]是否由s1[0...i-1]和s2[0...j-1]的字符组成。
自然,我们的想法是遍历s3中的每个元素,然而要如何找到递推关系呢?
因为只需要输出true或false,那么我们可以只计算true的情形,其余情况全是false。
假设dp[i-1][j]为true,那么dp[i][j]为true的条件就是s1[i-1]是否等于s3[i+j-1]。
假设dp[i][j-1]为true,那么dp[i][j]为true的条件就是s2[j-1]是否等于s3[i+j-1]。 -
由此递推关系就可以求出:
dp[i][j]= (dp[i][j-1] && str2[j-1]==str3[i+j-1]) || (dp[i-1][j] && str1[i-1]==str3[i+j-1]) -
Python 代码:
def isInterleave(s1, s2, s3): m = len(s1) n = len(s2) k = len(s3) if k != m + n: return False dp = [[False for i in range(n + 1)] for i in range(m + 1)] dp[0][0] = True # if s1[0] == s3[0]: # dp[1][0] = True # if s2[0] == s3[0]: # dp[0][1] = True for i in range(m+1): for j in range(n+1): if i != 0 or j != 0: if dp[i-1][j] is True and s1[i-1] == s3[i+j-1]: dp[i][j] = True elif dp[i][j-1] is True and s2[j-1] == s3[i+j-1]: dp[i][j] = True else: dp[i][j] = False return dp[i][j] s1 = "xyz" s2 = "abc" s3 = "xyzabc" print(isInterleave(s1, s2, s3))
13、矩阵链乘积
矩阵链乘积(英语:Matrix chain multiplication,或Matrix Chain Ordering Problem,MOCP)是可用动态规划解决的最佳化问题。给定一序列矩阵,期望求出相乘这些矩阵的最有效方法。此问题并不是真的去执行其乘法,而只是决定执行乘法的顺序而已。
-
因为矩阵乘法具有结合律,所有其运算顺序有很多种选择。换句话说,不论如何括号其乘积,最后结果都会是一样的。例如,若有四个矩阵ABCD,将可以有:
ABCD = (AB)(CD) = A(BC)D = AB(CD) ... 但括号其乘积的顺序是会影响到需计算乘积所需简单算术的数目,假定各矩阵维数分别为 10x100 100x5 5x50,如果按 ((AB)C) 的加括号方式,要执行7500次标量乘法,而按(A(BC))的加括号方式,要执行75000次标量乘法。
那要如何决定n个矩阵相乘的最佳顺序呢?可以比较每一顺序的运算量(使用蛮力),但这将需要时间O(2^n),是一种非常慢且对大n不实在的方法。那解决方法,如我们将看到的,是将问题分成一套相关的子问题。以解答子问题一次而再使用其解答数次,即可以彻底地得出其所需时间。此一方法称为动态规划。
-
动态规划算法步骤:
- 首先思考:若只有两个矩阵相乘,则只会有一种方法去乘它们,所有其最小成本为乘积的成本,那么接下来可以按照如下方法计算。
- 取得矩阵的序列且将其分成两个子序列。
- 找出乘完每一子序列的最小成本。
- 将成本加起来,并加上两个结果矩阵相乘的成本。
- 在每一矩阵序列可分开的位置运作,并取其最小值。
-
总结成状态转移方程即为:
m[i,j] = 0 i=j m[i,j] = min{m[i,k]+m[k+1,j]+Pi-1PkPj} i
m[i,j] 为 A1A2...Aj 的最优完全加括号所需的最少标量乘法次数,对于整个问题来说,计算 A1...n 的最节省方式的代价自然应为 m[1,n]
Pi-1PkPj 是计算 Ai...k 和 Ak+1...j 的积所消耗的时间
-
伪代码:
Matrix-Chain-Order(int p[]) { n = p.length - 1; for (i = 1; i <= n; i++) m[i,i] = 0; for (l=2; l<=n; l++) { // l is chain length for (i=1; i<=n-l+1; i++) { j = i+l-1; m[i,j] = MAXINT; for (k=i; k<=j-1; k++) { q = m[i,k] + m[k+1,j] + p[i-1]*p[k]*p[j];//Matrix Ai has the dimension p[i-1] x p[i]. if (q < m[i,j]) { m[i,j] = q; s[i,j] = k; } } } } }- 稍加考察,可以知道运行时间为 Θ(n^3),辅助空间为 Θ(n^2)
上述过程除了确定最少标量乘法数,还计算了用于构造最优解的表格 s[1..n,1..n] 。每一项s[i,j]记录了AiAi+1...Aj的最佳加括号的在Ak和Ak+1之间分裂的值k,于是我们知道最终矩阵积A1..n的最佳计算是A1..s[1,n] As[1,n]+1..n。
-
于是可以有打印过程:
PRINT-OPTIMAL-PARENS(s,i,j) if i = j then print "A"i else print "(" PRINT-OPTIMAL-PARENS(s,i,s[i,j]) PRINT-OPTIMAL-PARENS(s,s[i,j]+1,j) print ")"