图论——拓扑排序

一、定义

AOV网络

  在有向图中，用顶点表示活动，用有向边i, V_j>表示活动 i 是活动 j 的先决条件。这种有向图称为用顶点表示活动的网络(Active on vertices)，记作AOV网络。 
  在AOV网络中，如果活动V_i必须在V_j之前进行，则存在有向边i, V_j>，并称V_i是V_j的直接前驱，V_j是V_i的直接后继。这种前驱与后继的关系具有传递性和反自反性，这要求AOV网络中不能出现回路，即有向环。因此，对于给定的AOV网络，必须先判断它是否存在有向环。

拓扑排序

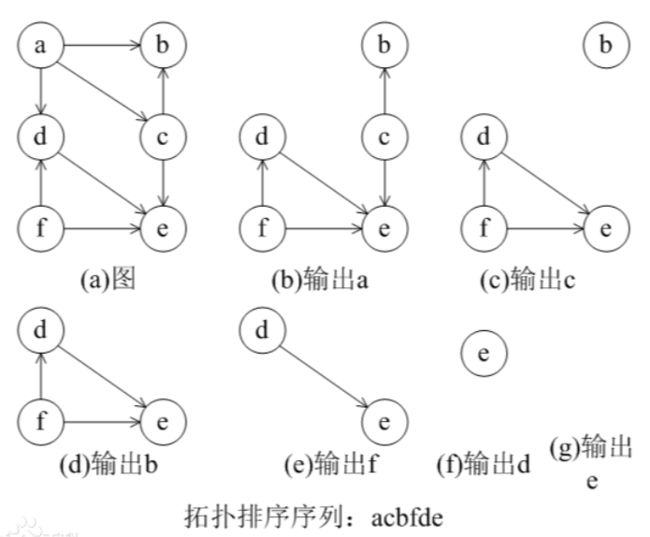
  检测有向环可以通过对AOV网络构造它的拓扑有序序列(即进行拓扑排序，topological sorting)。该过程将各个顶点排列成一个线性有序的序列，使得AOV网络中所有的前驱和后继关系都能得到满足。 
  如果拓扑排序能够将AOV网络的所有顶点都排入一个拓扑有序的序列中，则说明该AOV网络中没有有向环，否则AOV网络中必然存在有向环。AOV网络的顶点的拓扑有序序列不唯一。可以将拓扑排序看做是将图中的所有节点在一条水平线上的展开，图的所有边都从左指向右。

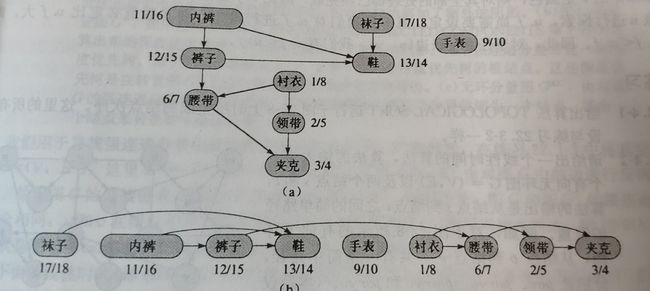
用穿衣服的次序来描述拓扑排序，图(a)表示必须先穿某些衣服，才可以穿其他衣服，图(b)表示将拓扑排序后的有向无环图在一条水平线上展示出来。

袜子和内裤属于同等级，在排序结果中谁先谁后无所谓，平常生活中也是如此（丝袜除外）。

 

翻译成人话

对于一个有向无环图

（1）：统计所有节点的入度，对于入度为0的节点就可以分离出来，然后把这个节点指向的节点的入度-1。

（2）：重复（1），直到所有的节点都被分离出来，拓扑排序结束。

（3）：如果最后不存在入度为0的节点，那就说明有环，无解。

 

时间复杂度

如果AOV网络有n个顶点，e条边，在拓扑排序的过程中，搜索入度为零的顶点所需的时间是O(n)。在正常情况下，每个顶点进一次栈，出一次栈，所需时间O(n)。每个顶点入度减1的运算共执行了e次。所以总的时间复杂为O(n+e)。

模板

因为拓扑排序的结果不唯一，所以使用了优先级队列，即得到的是最小字典序的结果。

#include 
#include 
#include 
#include 
#include 
using namespace std;

vector<int>head[505];
int in[505];

int main() {
    int n, m;
    cin >> n >> m;
        priority_queue<int, vector<int>, greater<int>>q;
        vector<int>ans;
        for (int i = 0; i < m; i++) {
            int c1, c2;
            scanf("%d%d", &c1, &c2);
            head[c1].push_back(c2);
            in[c2]++;
        }
        for (int i = 1; i <= n; i++) {
            if (!in[i]) {
                q.push(i);
            }
        }

        while (!q.empty()) {
            int temp = q.top(); q.pop();
            ans.push_back(temp);
            for (int i = 0; i < head[temp].size(); i++) {
                in[head[temp][i]]--;
                if (!in[head[temp][i]])
                    q.push(head[temp][i]);
            }
        }
        if (ans.size() == n) {
            for (int i = 0; i < n; i++) {
                head[i + 1].clear();
                cout << ans[i];
                if (i != n - 1)cout << ' ';
            }
            cout << endl;
        }
    return 0;
}

View Code

二、练习

例题一：

没有花头的模板题: http://acm.hdu.edu.cn/showproblem.php?pid=1285

代码：

#include 
#include 
#include 
#include 
#include 
using namespace std;

vector<int>head[505];
int in[505];

int main() {
    int n, m;
    while (cin >> n >> m) {
        priority_queue<int, vector<int>, greater<int>>q;
        vector<int>ans;
        for (int i = 0; i < m; i++) {
            int c1, c2;
            scanf("%d%d", &c1, &c2);
            head[c1].push_back(c2);
            in[c2]++;
        }
        for (int i = 1; i <= n; i++) {
            if (!in[i]) {
                q.push(i);
            }
        }

        while (!q.empty()) {
            int temp = q.top(); q.pop();
            ans.push_back(temp);
            for (int i = 0; i < head[temp].size(); i++) {
                in[head[temp][i]]--;
                if (!in[head[temp][i]])
                    q.push(head[temp][i]);
            }
        }
        if (ans.size() == n) {
            for (int i = 0; i < n; i++) {
                head[i + 1].clear();
                cout << ans[i];
                if (i != n - 1)cout << ' ';
            }
            cout << endl;
        }
        q.emplace();
        ans.clear();
        
    }
    
    return 0;
}

View Code

例题二：

反向拓扑排序： http://acm.hdu.edu.cn/showproblem.php?pid=4857

原文链接：https://blog.csdn.net/Lawliet1993/article/details/51043070

题意：n个结点，m个拓扑关系（a，b）表示a必须排在b前面，在满足m个拓扑关系关系的前提下使得小的结点尽可能的排在前面。也就是说我们现在要从1号结点开始考虑，如果要排1号结点，根据拓扑关系，首先必须排哪些结点，如果排好了1号结点，则继续考虑2号结点 ，3号结点。。
我们先看两个例子：
存在拓扑关系：
5 -> 3 -> 1
6 -> 4 -> 2
直接拓扑排序的结果是 5 3 1 6 4 2，结果是正确的（1号尽可能的在前面了） ，看起来好像直接拓扑排序就可以了，但是为什么提交后却wa了呢，别急，我们再看一个例子：
6 -> 3 -> 1
5 -> 4 -> 2
直接拓扑排序的结果是：5 4 2 6 3 1 ，结果是错误的，因为我们可以把1号安排到更前面的位置 即：6 3 1 5 4 2（正确答案）。
看到这里应该就知道为什么直接拓扑排序不行了吧，我们分析一下为什么会出现这样的状况，对于多条弧或者边，我们是先删除弧尾结点比较小的结点即（5号结点比6号结点小,先删除以该点为尾的弧），而这也正是问题所在，我们希望的是优先删除弧头比较小的弧的（1号结点比2号结点小，因优先删除以1号为头的弧）。
好了，问题找到了，现在我们在来想如何解决问题，我们可以尝试一下逆向思维，即我们先考虑哪些点应该靠后释放，这样的话我们就可以把拓扑关系反过来（即弧头和弧尾调换），然后做拓扑排序，然后我们可以根据原来的弧头(现在变成弧尾)的大小来释放结点，由于现在的问题变成哪些最后释放，那么就应该优先考虑弧尾（原来的弧头）比较大的，可以通过优先队列来解决。

#include 
#include 
#include 
#include 
#include 
using namespace std;

vector<int>head[30005];
int in[30005];

int main() {
    int T;
    cin >> T;
    while (T--) {
        int n, m;
        cin >> n >> m;
        priority_queue<int>q;
        vector<int>ans;
        for (int i = 0; i < m; i++) {
            int c1, c2;
            scanf("%d%d", &c1, &c2);
            /*head[c1].push_back(c2);
            in[c2]++;*/
            head[c2].push_back(c1);
            in[c1]++;
        }
        for (int i = 1; i <= n; i++) {
            if (!in[i]) {
                q.push(i);
            }
        }

        while (!q.empty()) {
            int temp = q.top(); q.pop();
            ans.push_back(temp);
            for (int i = 0; i < head[temp].size(); i++) {
                in[head[temp][i]]--;
                if (!in[head[temp][i]])
                    q.push(head[temp][i]);
            }
        }

        if (ans.size() == n) {
            for (int i = n - 1; i >= 0 ; i--) {
                head[i + 1].clear();
                cout << ans[i];
                if (i != 0)cout << ' ';
            }
            cout << endl;
        }
        q.emplace();
        ans.clear();
    }
    return 0;
}

View Code