用于解决动态连通图的连接性问题
问题描述
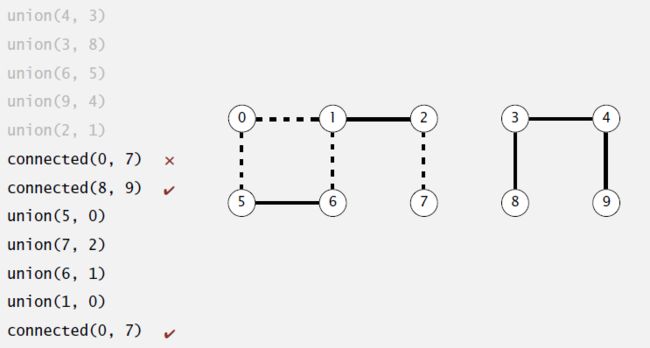
给定由N个对象构成的集合,并告知哪些对象之间是连通的,由此判断某两个对象之间是否连通。
注:连通代表有路可达,而不一定直接相连
抽象建模
- 将所有对象用序号标识,如0,1,2,3...
- Union 将告知的连通对象之间连通
- Find 判断某两个对象之间是否连通
算法描述
基本思想是,将连通图分割成N个最大连通子集,即每个子集内部的对象相互连通,而子集之间的对象互不连通,这样只需判断某两个对象是否在同一个子集中,便可判断其是否连通。
具体而言,根据不同的实现方式,可衍生出以下几种算法。
1. Quick-Find
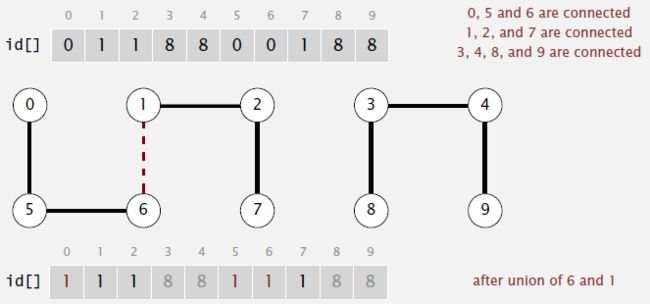
顾名思义,这是一个注重快速判断的算法。它将属于同一个子集的对象用同一个标号标识,而不同子集用不同标号标识,这时判断对象是否连通就等价于判断对象标号是否相等。
实现思路
- 整形N维数组id[],存储N个对象所属的子集标号,下标为对象标识
- Union 合并分别包含p和q的子集,需将所有标号等于id[p]的都置为id[q]
- Find 判断p和q是否连通,即判断是否满足id[p]==id[q]
伪代码
// 初始化 function(int N)
id = new int[N];
for (int i = 0; i < N; i++)
id[i] = i; // 每个对象在初始时各不连通,各成一个子集,用其下标标识
// Union function(int p, int q)
int pid = id[p];
int qid = id[q];
for (int i = 0; i < N; i++)
{
if (id[i] == pid)
id[i] = qid; // 将所有子集标识等于id[p]的改为id[q]
}
// Find function(int p, int q)
return id[p] == id[q]; // 判断子集标识是否相同
这种算法虽然Find很快,但Union却非常慢,每次需要判断和改动的位置很多。一般来说,Union的次数要比Find的次数多很多,所以注重Union效率的提高会更实际一些。
2. Quick-Union
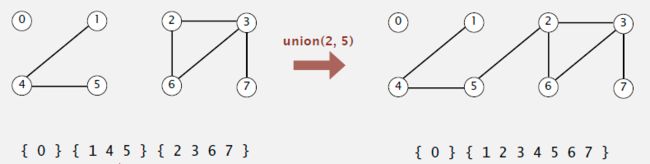
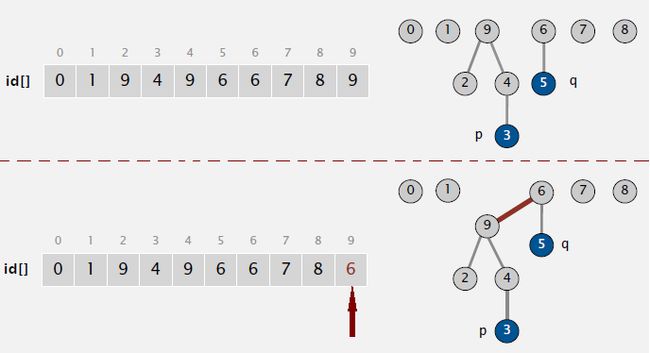
这即是一个注重快速合并的算法, 不同于Quick-Find将子集内所有对象都用同一个标识表示,它将子集中的对象看成是树状结构,每个子集形成一棵树,子集中的对象都有父对象,根对象的父对象是其自身。
此时,在N维数组中存储各对象的父对象标识,则对象i所在子集树的根为id[id[id[...id[i]...]]],同一个根对应的所有对象是连通的。这样,Find时需判断对象的根是否相同,而Union时只需将一个子集树的根变为另一个子集树的孩子。可见,Union时只需要变更一个位置,而Find则取决于树的高度。
伪代码
// Root function(int i)
while (i != id[i]) i = id[i]; // 寻找根节点
return i;
// Union function(int p, int q)
int i = root(p);
int j = root(q);
id[i] = j; // 将一颗子集树挂在另一颗子集树根上
// Find function(int p, int q)
return root(p) == root(q); // 判断对象根节点是否相同
虽然这种算法的Union速度加快,但其速度仍取决于root的速度,即树的高度,因此可优化的地方还有很多。
3. Weighted Quick-Union
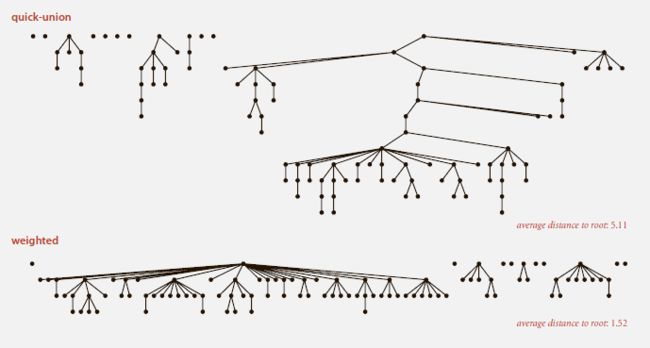
这是一个基于QU的加权算法,它可有效降低树的高度,使root速度变快。
其思想是,在每次Union合并子集树时,总是将小树的根挂在大树的根上,而不像QU中总是将前一个树的根挂在后一个树的根上。
这就需要另外设置一个N维整形数组,用于存储以每个对象为根的树大小,这样在Union时便可比对子集树的大小。
伪代码
// 初始化 function(int N)
sz = new int[N]; // 树大小数组
for (int i = 0; i < N; i++)
sz[i] = 1; // 初始时各对象自成一树,每棵树的大小为1
// Union function(int p, int q)
int i = root(p);
int j = root(q);
if (sz[i] < sz[j])
{
id[i] = j;
sz[j] += sz[i];
}
else
{
id[j] = i;
sz[i] += sz[j];
}
这种算法带来的压缩树高度的效果是非常显著的,尤其是在对象个数较多时。
4. Quick-Union with Path Compression
这是一种基于QU的路径压缩优化算法,目的也是压缩树的高度。
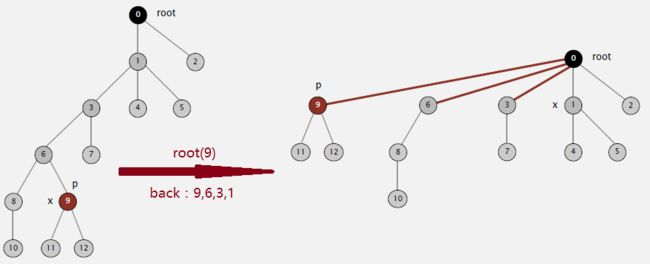
一种思想是,在每次寻找对象的根节点时,都将通往根节点的沿途各个节点直接挂在根节点下。代码实现可设置两个循环,先找根节点,再挂各节点。
另一种思想是,在每次寻找对象的根节点时,都将对象挂在其祖父对象上,再从祖父对象依次重复上述过程。则每次root会大致将路径长度压缩一半。
伪代码
// Root function(int i)
while (i != id[i])
{
id[i] = id[id[i]];
i = id[i];
}
return i;
当然也可以将Weighted与Path Compression结合使用。
5. Weighted Quick-Union with Path Compression
Weighted是在Union阶段,而Path Compression是在Root阶段,两者互不干扰,可结合使用,效果更好。
伪代码(完整)
/* Weighted Quick-Union with Path Compression */
// 初始化 function(int N)
id = new int[N]; // 父对象数组
sz = new int[N]; // 树大小数组
for (int i = 0; i < N; i++)
{
id[i] = i;
sz[i] = 1;
}
// Root function(int i)
while (i != id[i])
{
id[i] = id[id[i]]; // 采用Path Compression第二种思想
i = id[i];
}
return i;
// Union function(int p, int q)
int i = root(p);
int j = root(q);
if (sz[i] < sz[j]) // 采用Weighted思想
{
id[i] = j;
sz[j] += sz[i];
}
else
{
id[j] = i;
sz[i] += sz[j];
}
// Find function(int p, int q)
return root(p) == root(q);
算法分析
现分析各算法的时间性能。
Quick-Find
UnionO(N),FindO(1)Quick-Union
UnionO(N),FindO(N)
主要耗时在root上Weighted-QU
UnionO(logN),FindO(logN)
树的高度不会超过logN(以2为底),考虑一个对象,其最开始树大小为1,每次其高度+1发生在其作为小树成员挂到大树根上,此时合并树的大小>=2倍小树大小,而小树最多不会翻倍logN次,所以高度最高不会超过logNQU + Path Compression
UnionO(logN),FindO(logN)
猜想:采用第二种思想时,每次可将路径压缩一半,则最终树的高度<=logN?Weighted-QU + Path Compression
<= c(N+MlogN) 接近于线性
N表示对象个数,M表示Union次数
logN表示N经过多少次log能到达1,如log16=3, log65536=4
| Algorithm | Initialize | Union | Find | Worst-Case Time |
|---|---|---|---|---|
| Quick-Find | N | N | 1 | MN |
| Quick-Union | N | N | N | MN |
| Weighted-QU | N | logN | logN | N + MlogN |
| QU + Path Compression | N | logN | logN | N + MlogN |
| Weighted-QU + Path Compression | N | log*N | log*N | N + Mlog*N |
注:Union和 Find列均指一次操作的最坏时间复杂度, Worst-Case Time表示 M次Union操作的最坏时间复杂度。
应用举例
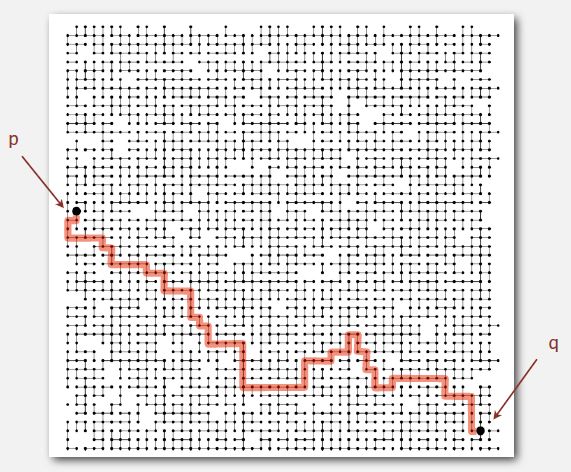
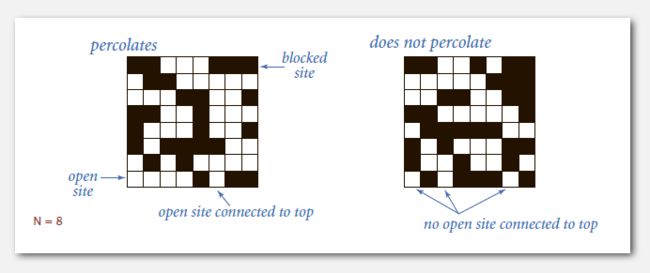
Union-Find 的一个典型应用是解决“渗透问题(Percolation)”
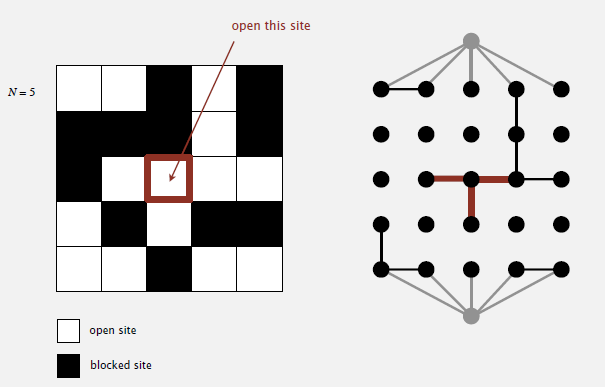
N*N的网格,网格中每一块都以概率p开启(白色)或关闭(黑色),判断从顶层能否渗透到底层(可假想从顶层注水,只能流经白色区域,水能否到达底层,或者导体通电问题等)
将每个网格看成是一个对象,这类问题明显可转化为动态连通图连接性问题,但要注意几个问题。
- 为避免循环,可将所有顶层节点与一个虚拟顶层节点相连,而将所有底层节点都与一个虚拟底层节点相连,这样只需判断两个虚拟节点是否连通。
- 开启一个网格时,应连通它与周围四个节点中所有开启的节点。
- Backwash问题,在将所有底层节点与虚拟底层节点相连后,如果要判断一个节点(不一定是底层节点)是否与顶层节点相连时,它可能会通过虚拟底层节点向上寻找到路径,这显然不符合常理。
可有两种解决方式,一是取消使用底层虚拟节点,牺牲时间;二是带虚拟底层几点与不带虚拟底层节点两种模型结合使用,牺牲空间。
结束语
动态连通图问题可以是很多问题的抽象建模,如网络中计算机连接、社交中的朋友关系、数学集合中的元素等等,掌握Union-Find的各算法是非常有用的。