背包问题
有N种物品和一个容量为W的背包。第i种物品的重量是w[i],价值是v[i]。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
三种背包
| No. | 分类 | 条件 |
|---|---|---|
| 1 | 0/1背包问题 | 每种物品只有一个 |
| 2 | 完全背包问题 | 每种物品有无穷个 |
| 3 | 多重背包 | 每种物品有有限个n[i] |
| No. | 分类 | 特点 |
|---|---|---|
| 1 | 状态 | 物品i,重量 |
| 2 | 结果 | 最大价值 |
| 3 | 状态转义 | 选择物品i,重量和价值增加 |
| 4 | 边界条件 | 没有可选的物品/所选物品超重 |
边界条件
| No. | 分类 | 说明 | 处理 |
|---|---|---|---|
| 1 | 遍历边界 | 数组边界 | 返回0 |
| 2 | 约束边界 | 超出约束 | 返回无效值(最值) |
模板
- 01背包问题
for(int i = 1;i <= n;++i){
for(int j = W;j >= w[i];--j){
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}
}
- 完全背包问题
for(int i = 0;i <= n;++i){
for(int j = w[i];j <= W;++j){
dp[j] = min(dp[j],dp[j-w[i]]+v[i]);
}
}
- 多重背包问题
朴素解法
for(int i = 0;i <= n;++i){
for(int k = 0;k < b[i];++k){
for(int j = W;j >= w[i];--j){
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}
}
}
举例
01背包问题
有4种物品和一个容量为4的背包。第i种物品的重量是4 3 1 1,价值是30 20 15 20。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
输入
4 4
30 20 15 20
4 3 1 1
参考代码
#include
using namespace std;
int knapsack_01(int n,int W,int* v,int* w){
int dp[W+1];
fill_n(dp,W+1,0);
for(int i=0;i<=n;++i){
for(int j=W;j>=w[i];--j){
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}
}
return dp[W];
}
int main() {
int N,W;
scanf("%d%d",&N,&W);
int v[N];
for(int i=0;i 完全背包问题
有4种物品和一个容量为4的背包。第i种物品的重量是4 3 1 1,价值是30 20 15 20。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
输入
4 4
30 20 15 20
4 3 1 1
参考代码
#include
using namespace std;
int knapsack_complete(int n,int W,int* v,int* w){
int dp[W+1];
fill_n(dp,W+1,0);
for(int i=0;i<=n;++i){
for(int j=w[i];j<=W;++j){
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}
}
return dp[W];
}
int main() {
int N,W;
scanf("%d%d",&N,&W);
int v[N];
for(int i=0;i 多重背包问题
有4种物品和一个容量为4的背包。第i种物品的重量是4 3 1 1,价值是30 20 15 20。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
输入
4 4
30 20 15 20
4 3 1 1
1 2 2 2
参考代码
- 朴素解法
#include
using namespace std;
int knapsack_limitnum(int n,int W,int* v,int* w,int* b){
int dp[W+1];
fill_n(dp,W+1,0);
for(int i=0;i<=n;++i){
for(int k=0;k=w[i];--j){
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}
}
}
return dp[W];
}
int main() {
int N,W;
scanf("%d%d",&N,&W);
int v[N];
for(int i=0;i - 二进制优化
#include
using namespace std;
int knapsack_01(int n,int W,int* v,int* w){
int dp[W+1];
fill_n(dp,W+1,0);
for(int i=0;i<=n;++i){
for(int j=W;j>=w[i];--j){
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}
}
return dp[W];
}
int knapsack_limitnum(int n,int W,int* v,int* w,int* b){
vector vv;
vector wv;
for(int i=0;i<=n;++i){
int count = b[i];
for(int j=1;j<=count;j<<1){
vv.push_back(v[i]*j);
wv.push_back(w[i]*j);
count-=j;
}
if(count>0){
vv.push_back(v[i]*count);
wv.push_back(w[i]*count);
}
}
return knapsack_01(vv.size()-1,W,vv.data(),wv.data());
}
int main() {
int N,W;
scanf("%d%d",&N,&W);
int v[N];
for(int i=0;i - 单调队列优化
#include
using namespace std;
int knapsack_limitnum(int n,int W,int* v,int* w,int* b) {
int dp[W+1];
fill_n(dp,W+1,0);
for (int i = 0; i <= n; i++) {
for (int j = 0; j < w[i]; j++){
deque p;
deque q;
for (int k = j, a = 0; k <= W; k += w[i],a++) {
if (p.size()==b[i]+1) {
if(q.front()==p.front()) q.pop_front();
p.pop_front();
}
int t = dp[k] - a*v[i];
p.push_back(t);
while (!q.empty() && t >= q.back()) q.pop_back();
q.push_back(t);
dp[k] = q.front() + a*v[i];
}
}
}
return dp[W];
}
int main() {
int N,W;
scanf("%d%d",&N,&W);
int v[N];
for(int i=0;i 总结
- 先枚举物品,再枚举容量
- 01背包问题,逆序枚举容量;完全背包问题,顺序枚举容量。
- 状态转移方程是
dp[j]=max(dp[j],dp[j-w[i]]+v[i])。 - 多重背包是
k个01背包问题。
1. 0/1背包问题
- NOI 1159:01背包问题
- 51nod 1085:01背包问题
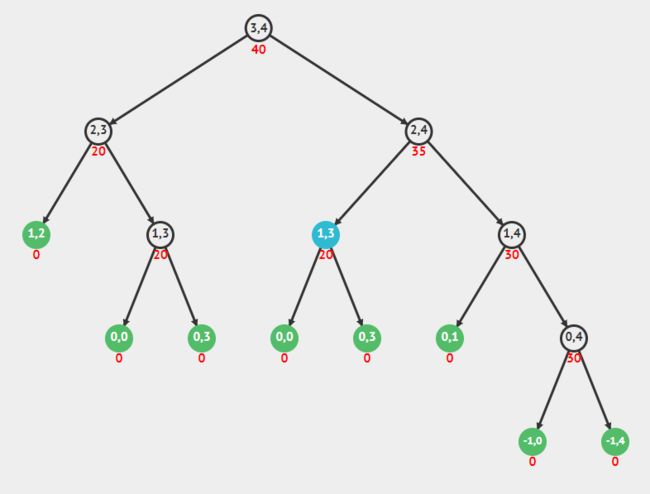
1.1 自顶而下(递归)
蓝色节点表示重复计算部分
#include
using namespace std;
int knapsack(int i, int w,int*weights,int*values,vector* dp) {
if (w == 0) // 刚好装下
return 0;
if (weights[i] > w) // 超重
return 0;
if (i < 0) // 没有物品
return 0;
// 选择第i件物品,剩余重量减少,总价值增加,且只能再选择下一件物品
// 不选择第i件物品,剩余重量不变,总价值不变,且只能再选择下一件物品
if(0 != dp[i][w]) return dp[i][w];
return dp[i][w] = max(knapsack(i - 1, w - weights[i],weights,values,dp) + values[i],
knapsack(i - 1, w,weights,values,dp));
}
int main(){
int n,t;
scanf("%d%d",&n,&t);
int weights[t];
int values[t];
for(int i=0;i dp[t];
fill_n(dp,t,vector(n+1,0));
printf("%d\n",knapsack(t-1,n,weights,values,dp));
}
1.2 自底而上(递推)
基本思路:先枚举物品,再枚举容量,如果有足够的容量,则添加进背包。
#include
using namespace std;
int knapsack(int t, int n,int*weights,int*values,vector* dp) {
for(int i=1;i= 0){// 放的下
dp[i][w] = max(dp[i-1][w-weights[i]] + values[i],dp[i-1][w]);
}else{// 放不下
dp[i][w] = dp[i-1][w];
}
}
}
return dp[t-1][n];
}
void Print(vector* dp,int t){
for(int i=0;i dp[t];
fill_n(dp,t,vector(n+1,0));
printf("%d\n",knapsack(t,n,weights,values,dp));
// Print(dp,t);
}
1.3 滚动数组优化
把原来的二维数组压缩成一个一维数组。
#include
using namespace std;
int knapsack(int t, int n,int*weights,int*values) {
int dp[n+1];
fill_n(dp,n+1,0);
for(int i=0;i<=t;++i)
for(int j=n ;j>=weights[i];--j)
dp[j] = max(dp[j] , dp[j - weights[i]]+values[i]);
return dp[n];
}
int main(){
int n,t;
scanf("%d%d",&n,&t);
int weights[t];
int values[t];
for(int i=0;i 2. 完全背包问题
- NOI 1160:完全背包问题
2.1 自顶而下(递归)
注意,可以重复选择
#include
using namespace std;
int knapsack(int i, int w,int*weights,int*values,vector* dp) {
if (w == 0) // 刚好装下
return 0;
if (weights[i] > w) // 超重
return 0;
if (i < 0) // 没有物品
return 0;
// 选择第i件物品,剩余重量减少,总价值增加,且只能再选择下一件物品
// 不选择第i件物品,剩余重量不变,总价值不变,且只能再选择下一件物品
if(0 != dp[i][w]) return dp[i][w];
return dp[i][w] = max(knapsack(i, w - weights[i],weights,values,dp) + values[i],
knapsack(i - 1, w,weights,values,dp));
}
int main(){
int n,t;
scanf("%d%d",&n,&t);
int weights[t];
int values[t];
for(int i=0;i dp[t];
fill_n(dp,t,vector(n+1,0));
printf("%d\n",knapsack(t-1,n,weights,values,dp));
}
2.2 自底而上(递推)
基本思路:先枚举物品,再枚举容量,如果有足够的容量,则添加进背包。注意,可以重复选择
#include
using namespace std;
int knapsack(int t, int n,int*weights,int*values,vector* dp) {
for(int i=1;i= 0){// 放的下
dp[i][w] = max(dp[i][w-weights[i]] + values[i],dp[i-1][w]);
}else{// 放不下
dp[i][w] = dp[i-1][w];
}
}
}
return dp[t-1][n];
}
void Print(vector* dp,int t){
for(int i=0;i dp[t];
fill_n(dp,t,vector(n+1,0));
printf("%d\n",knapsack(t,n,weights,values,dp));
// Print(dp,t);
}
2.3 滚动数组优化
#include
using namespace std;
int knapsack(int t, int n,int*weights,int*values) {
int dp[n+1];
fill_n(dp,n+1,0);
for(int i=0;i<=t;++i)
for(int j=weights[i] ;j<=n;++j)
dp[j] = max(dp[j] , dp[j - weights[i]]+values[i]);
return dp[n];
}
int main(){
int n,t;
scanf("%d%d",&n,&t);
int weights[t];
int values[t];
for(int i=0;i 3. 多重背包问题
51nod 1086:多重背包问题
二进制优化
#include
using namespace std;
int knapsack_01(int n,int W,int* v,int* w){
int dp[W+1];
fill_n(dp,W+1,0);
for(int i=0;i<=n;++i){
for(int j=W;j>=w[i];--j){
dp[j] = max(dp[j],dp[j-w[i]]+v[i]);
}
}
return dp[W];
}
int knapsack_limitnum(int n,int W,int* v,int* w,int* b){
vector vv;
vector wv;
for(int i=0;i<=n;++i){
int count = b[i];
for(int j=1;j<=count;j<<1){
vv.push_back(v[i]*j);
wv.push_back(w[i]*j);
count-=j;
}
if(count>0){
vv.push_back(v[i]*count);
wv.push_back(w[i]*count);
}
}
return knapsack_01(vv.size()-1,W,vv.data(),wv.data());
}
int main() {
int N,W;
scanf("%d%d",&N,&W);
int v[N];
int w[N];
int b[N];
for(int i=0;i - 单调队列优化
#include
using namespace std;
int knapsack_limitnum(int n,int W,int* v,int* w,int* b) {
int dp[W+1];
fill_n(dp,W+1,0);
for (int i = 0; i <= n; i++) {
for (int j = 0; j < w[i]; j++){
deque p;
deque q;
for (int k = j, a = 0; k <= W; k += w[i],a++) {
if (p.size()==b[i]+1) {
if(q.front()==p.front()) q.pop_front();
p.pop_front();
}
int t = dp[k] - a*v[i];
p.push_back(t);
while (!q.empty() && t >= q.back()) q.pop_back();
q.push_back(t);
dp[k] = q.front() + a*v[i];
}
}
}
return dp[W];
}
int main() {
int N,W;
scanf("%d%d",&N,&W);
int v[N];
int w[N];
int b[N];
for(int i=0;i 动态演示
VisualGo测试数据
i=3,w=4
[30,20,15,20]
[4,3,1,1]
蓝色节点表示重复计算部分
/* base caseS */
if (w == 0 || i < 0) return 0;
if (a2[i] > w) return f(i-1, w);
/* recursive caseS */
return Math.max(
a1[i] + f(i-1, w-a2[i]), /* take */
f(i-1, w)); /* not take */
蓝色节点表示重复计算部分
/* base caseS */
if (w == 0 || i < 0) return 0;
if (a2[i] > w) return 0;
/* recursive caseS */
return Math.max(
a1[i] + f(i-1, w-a2[i]), /* take */
f(i-1, w)); /* not take */
混合背包
有的物品只可以取一次(01背包),有的物品可以取无限次(完全背包),有的物品可以取的次数有一个上限(多重背包)
for(int i=1;i<=n;i++)
{
if(第i件物品是01背包)
for(int j=V;j>=c[i];j--)
f[j] = max(f[j],f[j-c[i]]+w[i]);
else if(第i件物品是完全背包)
for(int j=c[i];j<=V;j++)
f[j] = max(f[j],f[j-c[i]]+w[i]);
else if(第i件物品是多重背包)
MutiplyPack();
}