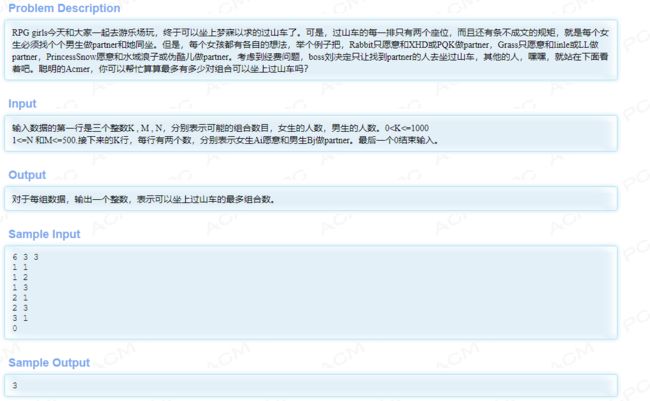
问题来源:Problem - 2063
思路分析:
这道题用到的算法是匈牙利算法,匈牙利算法的目的就是求二分图最大匹配的算法。
这位老哥写的匈牙利算法就简单易懂:https://blog.csdn.net/sunny_hun/article/details/80627351
以这道题的分析来说,假设女生集合有A={A1,A2,A3},男生集合有B={B1,B2,B3},存在关系{{A1,B1},{A1,B2},{A1,B3},{A2,B1},{A2,B3},{A3,B1}}。
从女生的角度出发,A1,A2都选择各自的第一组关系{A1,B1},{A2,B3},接下来看A3,存在B1已经被人选择了的情况,因此,我们返回B1,查看选择B1关系的女生A1是否还有其他关系可以选择,发现A1,存在关系{A1,B2},那么A3就可以选择关系{A3,B1},这样就选出的二分图的最大匹配,3组关系
多组关系也是使用同种方法,依次类推,直至找到最大匹配
实现代码
import java.util.Scanner;
public class Test_2063 {
static int line[][];
static int used[];
static int boy[];
static int k;
static int m;
static int n;
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
while(in.hasNextInt()) {
k = in.nextInt();
if(k == 0)
break;
m = in.nextInt();
n = in.nextInt();
line = new int[505][505];
used = new int[505];
boy = new int[505];
int sum = 0;
while(k-- > 0) {
int a = in.nextInt();
int b = in.nextInt();
line[a][b] = 1;
}
for(int i=1;i<=m;i++) {
for(int j=1;j<=m;j++) {
used[j] = 0;
}
if(find(i))
sum++;
}
System.out.println(sum);
}
}
public static boolean find(int x) {
for(int j=1;j<=n;j++) { //扫描每个男生
if(line[x][j] == 1 && used[j] == 0) {
used[j] = 1;//如果女生x选择了男生j,且男生j还没有被选择,则把男生j标记
if(boy[j] == 0 || find(boy[j])) {
boy[j] = x;//如果男生j没有搭档,那么男生j的匹配就是女生x
return true;
}
}
}
return false;
}
}