摄影测量与计算机视觉--相机模型与成像几何
前言
总体而言,摄影测量与计算机视觉在相机模型和成像几何上有许多的共通之处,尤其是在CCD/CMOS普及之后两者的差别逐渐变小。然而由于摄影测量发源于胶片相机时代并且摄影测量通常是俯视拍摄(即利用航空飞机从上向下拍摄)等等历史原因,摄影测量和计算机视觉两者在相机模型上还是有略微区别。
本次将主要讲解两者的相机模型与成像几何,并展示两者的差异。
摄影测量
前文已经提到,摄影测量的主要目的还是利用摄影技术进行测量,所以其主要目的是保证测量的精度和准确。因此早期(现在也依然如此)摄影测量通常会使用专业的摄影测量仪进行拍摄,从而尽可能保证拍摄影像的质量和精度(畸变较小)。最开始摄影测量仪主要是框幅式光学航空摄像仪(胶片时代),后期逐渐开始使用基于CCD/CMOS的数字航空成像仪,现在随着无人机、近景摄影测量的发展,在摄影测量中使用普通相机的情况也逐渐增多。
框幅式光学航空成像仪是摄影测量界的元老级仪器,虽然现在能够接触到该仪器的概率已经不大;但是摄影测量学的理论发展多来自于此时代,因此后文在讲解系列概念时会同时估计胶片成像和数字成像。
无论是胶片成像还是数字成像,其成像原理都是小孔成像,下边画了一个胶片成像的示意图(数字成像一样):
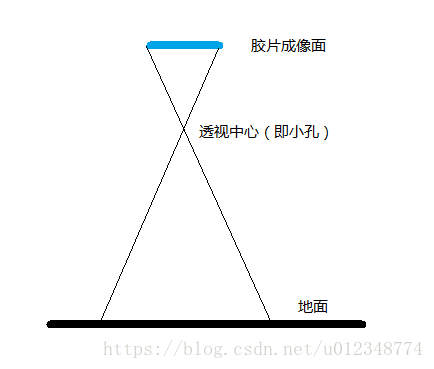
接下来将分为畸变问题、成像坐标系、相机内参数、相机外参数表示和成像几何5个方面分别展开讲解。
畸变问题
在胶片成像时代,由于此时相机结构相对简单,其畸变的产生原因通常来源于胶片没有恰当的安装,出现了不平整等等问题。为解决该问题,摄影测量的方法是在照片四周设计框标,并根据框标来校正胶片安装的问题。其原理是胶片上框标间的距离是固定的,因此利用多项式来修复距离的变化。下图展示了一副航片和对应的框标。
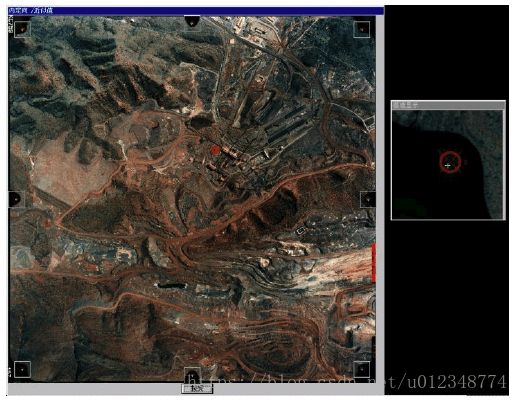
在数字成像时代,此时成像原件已经变化为CCD/CMOS,其畸变产生的原因较为复杂;并且受到计算机视觉的影响,摄影测量学中也开始使用桶形畸变、枕形畸变等等来解决畸变问题。在此方面,计算机视觉和摄影测量的差异较小,相关内容将放到计算机视觉部分讲解。下图展示了两种畸变的效果图。


成像坐标系
成像坐标系是描述成像几何的基础。在摄影测量中,有三个比较重要的成像坐标系分别是图像坐标系、像平面坐标系和像空间坐标系。
图像坐标系是描述图像上内容在图片上位置的坐标系。目前最常用的是其原点在图片左上角,然后 x x 轴水平向右, y y 轴垂直向下,图示如下:

像平面坐标系是定义在成像平面上的右手平面坐标系,其原点在主点(投影中心在像平面上的投影),其 x x 轴向右, y y 轴向上,图示如下:
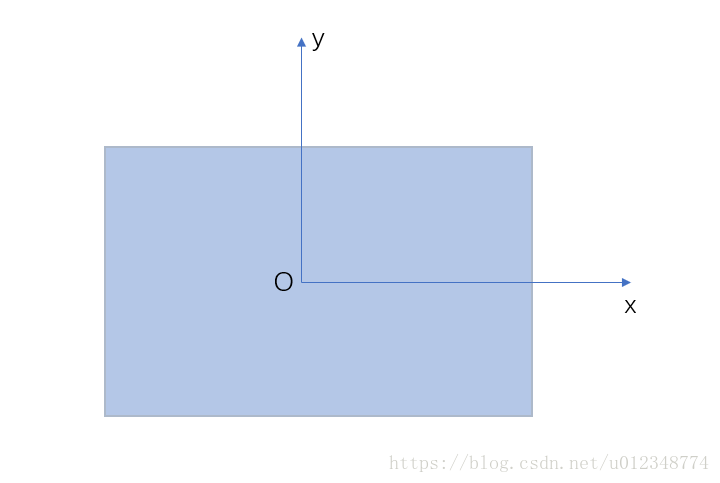
像空间坐标系是建立在投影中心上的右手三维坐标系,其 x x 轴、 y y 轴与像平面坐标系平行,图示如下(注意成像面在负轴方向):
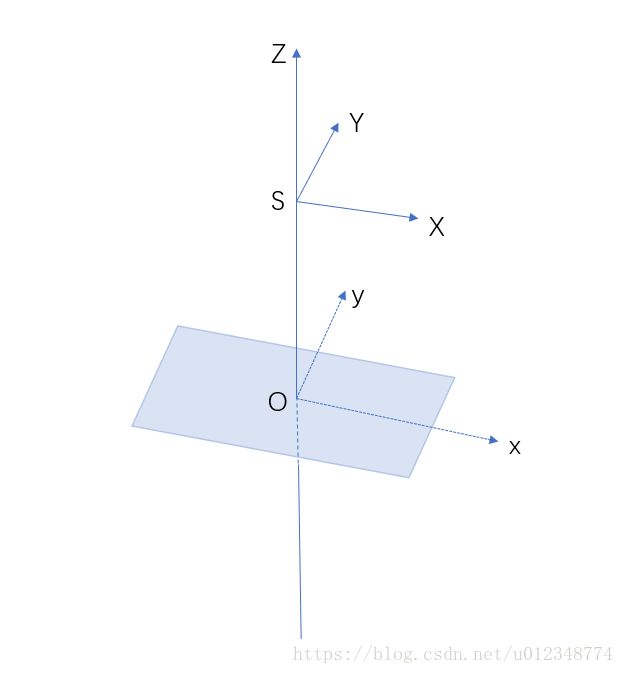
这里我们要格外探讨一下两个坐标系的单位。在胶片成像时代,由于是在胶片上直接测量,因此两个坐标系的单位毋庸置疑的是米(m)。但是在数字成像时代,我们并不能直接在CCD/CMOS上进行测量,而是在对应的照片上测量,获取到的坐标都是像素坐标,因此此时两个坐标系的单位就变成了像素(pixel)。表面上看起来两种表达方式的差异特别大,其实两者没有任何差别,因为在后续的成像表达式中就可以发现,单位可以被约掉(参考共线方程)。并且决定你究竟使用物理坐标还是像素坐标的核心在于你使用的焦距是物理焦距还是像素焦距!!!
相机内参数
相机内参数是描述相机成像几何的关键参数,通常包括主点位置和焦距。
主点位置就是像平面坐标系的原点在图片上的像素坐标(或者物理坐标),通常再经过畸变改正后都位于图像的正中心。
焦距是描述投影中心到成像平面的距离,不过焦距的单位可以是物理距离也可以是像素距离,只需要保证与图像坐标系的描述一致即可。
相机外参数
相机的外参数主要是描述相机相对于世界坐标系的位置,通常需要使用6个自由变量(三个位置变量和三个角度变量,位置变量描述相机在世界坐标系中的位置,角度变量描述相机的朝向)来描述。在摄影测量中,位置变量使用一个三维向量表示,角度变量使用OPK表示(关于角度变量后续我会另外整理一篇文档介绍,此处就简单使用OPK;当然还有POK等等,但都是欧拉角表示)。
摄影测量是一个非常注重几何解释的学科,因此其使用的6个自由变量都可以通过几何表达的方式展现出来:
1. 位置变量:像空间坐标系的原点在世界坐标系中的坐标;
2. 角度变量:世界坐标系分别依次绕x->y->z轴逆时针旋转(从坐标轴正向看向原点)到与像空间坐标系三轴平行的状态所旋转的角度;这里有一个地方需要解释一下,此时我们描述的时候旋转的是坐标系,但是在公式表达是我们旋转的是坐标值,两个之间存在一个逆过程。假设记OPK对应的旋转矩阵为
补充介绍一下OPK和POK。OPK是国外摄影测量通用的方式,其定义是依次绕x->y->z轴逆时针旋转(从坐标轴正向看向原点);POK是国内常用的方式,其定义是一次绕y->x->z旋转,其中第一次为逆时针,后两次都为顺时针(很多人可能会好奇为啥第一次要逆时针,后两次是顺时针,其实你列一下旋转矩阵就会发现,逆时针绕y轴旋转的旋转矩阵与x、z轴逆时针旋转的旋转矩阵形式存在一个差异,即对角线的sin负号位置不统一;国内为了保证旋转矩阵类似,所以做了这么一个改变)。下图中是POK的定义,可以发现sin的负号都在右上角:
成像几何
成像几何的主要内容是描述世界坐标系中的一点是如何投影到相片上去的。
在摄影测量中有一个非常形象化的过程:首先将该点所在坐标系平移到投影中心处;然后对其坐标系进行旋转;然后经过一个投影相似变换即可得到投影坐标。
上述步骤用公式可以表达如下 (X,Y,Z) ( X , Y , Z ) 是物方点坐标, (x,y) ( x , y ) 是其对应的投影点坐标;相机的外参数分别用 (Xs,Ys,Zs) ( X s , Y s , Z s ) 、 RT R T (前文已经解释为什么要求逆)表示。
首先平移:
然后旋转
把上述公式整理一下就可以得到:
共线返程是摄影测量的核心,其后续的所有研究都是围绕其展开得到了,需要特别注意!
计算机视觉
成像几何在计算机视觉中也是非常重要的内容。为了与摄影测量形成对比,此处也分别从畸变问题、成像坐标系、相机内参数、相机外参数表示和成像几何5个方面来解释计算机视觉中的相机模型与成像几何。与摄影测量相比,计算机视觉在描述问题时都尽可能使用矩阵的形式来简化。
畸变问题
在计算机视觉中,畸变问题是一个得到了非常多学者研究的问题,从畸变问题的建模到畸变参数的求解,每一个部分都得到非常细致的研究。不过总体而言,目前最为流行的畸变模型分别是径向畸变和切向畸变,其畸变参数分别用 k1 k 1 、 k2 k 2 和 p1 p 1 、 p2 p 2 来表示,其数学模型如下:
成像坐标系
与摄影测量对应,计算机视觉中也有一些非常重要的成像坐标系,分别是图像坐标系、成像平面坐标系和相机坐标系。
图像坐标系的定义与摄影测量中的定义是相同的,其原点都位于图像的左上角。
成像平面坐标系的定义是原点在投影中心在成像面上的投影点, x x 与 y y 都与图像坐标系平行的坐标系。(注意与摄影测量像平面坐标系的区别)
相机坐标系是定义在投影中心, X X 轴与图像坐标系 x x 平行, Y Y 轴与图像坐标系 y y 平行的右手坐标系。(注意与摄影测量像空间坐标系的区别),图示如下(即成像平面在z轴的正半轴):
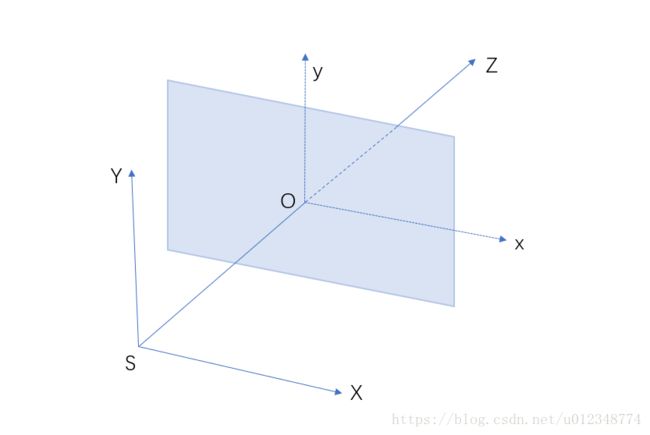
相机内参数
在计算机视觉中,相机内参数的内容与摄影测量相似的。不过不同之处在于,计算机视觉中更加偏向于用矩阵的形式统一表达,因此其内参数可以用矩阵 K K 来表示
通过 K K 矩阵即可完成成像平面坐标系到图像坐标系的转换。
相机外参数
由于相机的自由度是6,因此计算机视觉也需要使用6个参数来表达相机的姿态。不过在计算机视觉中,更加偏重的是表达的一致性和简洁性,使用的参数往往不具有明确的几何意义,因此在此处不做过多的几何解释。但是其外参数也可以分为平移部分和旋转部分。
1. 平移部分,在计算机视觉中平移部分在公式中体现为 t t ,然而其没有直接的几何意义,有几何意义的量是 C=−Rtt C = − R t t ,此处的C对应的就是投影中心在世界坐标系中的位置;
2. 旋转部分,关于旋转的表达,计算机视觉领域有非常独特的见解。他们认为欧拉角虽然符合人的直觉,但是在数学上却存在很多缺陷,例如存在万向节锁死问题(怎么理解,就是在特殊情况下只需要绕着两个轴即可完成旋转,这会造成解的奇异性);因此他们在旋角系统上下了很多功夫,提出了扭转系数、四元数和李代数等等非常优秀的旋角表示工具。与旋角相关的介绍将在后文展开,此处就不细讲。
成像几何
计算机视觉中的成像几何过程基本和摄影测量类似,此处也不再赘述。不过在计算机视觉中,为了对齐投影过程,使用了齐次坐标,因此整个投影过程可以用一个矩阵变换来表达,如下:
其中
总结
在本博客中主要介绍了摄影测量和计算机视觉中相机模型与成像几何。不难发现,两者在CCD/CMOS发展时代的相似度非常高。
但是两者还是存在一些差异,摄影测量的共线方程和计算机视觉的 P P 矩阵中的变量的含义是完全不对应的,这一点值得特别注意。另外关于如何进行两者的转换,请参考我的另外一篇博客“摄影测量与计算机视觉–几何差异和转换“。