PyTorch动态神经网络

PyTorch 是 PyTorch 在 Python 上的衍生. 因为 PyTorch 是一个使用 PyTorch 语言的神经网络库, Torch 很好用, 但是 Lua 又不是特别流行, 所有开发团队将 Lua 的 Torch 移植到了更流行的语言 Python 上. 是的 PyTorch 一出生就引来了剧烈的反响. 为什么呢?

而且如果你知道 Numpy, PyTorch 说他就是在神经网络领域可以用来替换 numpy 的模块.

PyTorch 和 Tensorflow 

据 PyTorch 自己介绍, 他们家的最大优点就是建立的神经网络是动态的, 对比静态的 Tensorflow, 他能更有效地处理一些问题, 比如说 RNN 变化时间长度的输出. 而我认为, 各家有各家的优势和劣势, 所以我们要以中立的态度. 两者都是大公司, Tensorflow 自己说自己在分布式训练上下了很大的功夫, 那我就默认 Tensorflow 在这一点上要超出 PyTorch, 但是 Tensorflow 的静态计算图使得他在 RNN 上有一点点被动 (虽然它用其他途径解决了), 不过用 PyTorch 的时候, 你会对这种动态的 RNN 有更好的理解.

而且 Tensorflow 的高度工业化, 它的底层代码… 你是看不懂的. PyTorch 好那么一点点, 如果你深入 API, 你至少能比看 Tensorflow 多看懂一点点 PyTorch 的底层在干嘛.

最后我的建议就是:

• 如果你是学生, 随便选一个学, 或者稍稍偏向 PyTorch, 因为写代码的时候应该更好理解. 懂了一个模块, 转换 Tensorflow 或者其他的模块都好说.
• 如果是上班了, 跟着你公司来, 公司用什么, 你就用什么, 不要脱群.

PyTorch安装

学习资料:

• PyTorch 官网

安装

PyTorch 安装起来很简单, 它自家网页上就有很方便的选择方式 (网页升级改版后可能和下图有点不同):

然后根据上面的提示, 我只需要在我的 Terminal 当中输入以下指令就好了:

$ pip install http://download.pytorch.org/whl/torch-0.1.11.post5-cp35-cp35m-macosx_10_7_x86_64.whl
$ pip install torchvision

Torch 或 Numpy

Torch 自称为神经网络界的 Numpy, 因为他能将 torch 产生的 tensor 放在 GPU 中加速运算 (前提是你有合适的 GPU), 就像 Numpy 会把 array 放在 CPU 中加速运算. 所以神经网络的话, 当然是用 Torch 的 tensor 形式数据最好咯. 就像 Tensorflow 当中的 tensor 一样.

当然, 我们对 Numpy 还是爱不释手的, 因为我们太习惯 numpy 的形式了. 不过 torch 看出来我们的喜爱, 他把 torch 做的和 numpy 能很好的兼容. 比如这样就能自由地转换 numpy array 和 torch tensor 了:

import torch
import numpy as np

np_data = np.arange(6).reshape((2, 3))
torch_data = torch.from_numpy(np_data)
tensor2array = torch_data.numpy()
print(
    '\nnumpy array:', np_data,          # [[0 1 2], [3 4 5]]
    '\ntorch tensor:', torch_data,      #  0  1  2 \n 3  4  5    [torch.LongTensor of size 2x3]
    '\ntensor to array:', tensor2array, # [[0 1 2], [3 4 5]]

Torch 中的数学运算 

其实 torch 中 tensor 的运算和 numpy array 的如出一辙, 我们就以对比的形式来看. 如果想了解 torch 中其它更多有用的运算符, API就是你要去的地方.

# abs 绝对值计算
data = [-1, -2, 1, 2]
tensor = torch.FloatTensor(data)  # 转换成32位浮点 tensor
print(
    '\nabs',
    '\nnumpy: ', np.abs(data),          # [1 2 1 2]
    '\ntorch: ', torch.abs(tensor)      # [1 2 1 2]
)

# sin   三角函数 sin
print(
    '\nsin',
    '\nnumpy: ', np.sin(data),      # [-0.84147098 -0.90929743  0.84147098  0.90929743]
    '\ntorch: ', torch.sin(tensor)  # [-0.8415 -0.9093  0.8415  0.9093]
)

# mean  均值
print(
    '\nmean',
    '\nnumpy: ', np.mean(data),         # 0.0
    '\ntorch: ', torch.mean(tensor)     # 0.0

除了简单的计算, 矩阵运算才是神经网络中最重要的部分. 所以我们展示下矩阵的乘法. 注意一下包含了一个 numpy 中可行, 但是 torch 中不可行的方式.

# matrix multiplication 矩阵点乘
data = [[1,2], [3,4]]
tensor = torch.FloatTensor(data)  # 转换成32位浮点 tensor
# correct method
print(
    '\nmatrix multiplication (matmul)',
    '\nnumpy: ', np.matmul(data, data),     # [[7, 10], [15, 22]]
    '\ntorch: ', torch.mm(tensor, tensor)   # [[7, 10], [15, 22]]
)

# !!!!  下面是错误的方法 !!!!
data = np.array(data)
print(
    '\nmatrix multiplication (dot)',
    '\nnumpy: ', data.dot(data),        # [[7, 10], [15, 22]] 在numpy 中可行
    '\ntorch: ', tensor.dot(tensor)     # torch 会转换成 [1,2,3,4].dot([1,2,3,4) = 30.0
)

新版本中(>=0.3.0), 关于 tensor.dot() 有了新的改变, 它只能针对于一维的数组. 所以上面的有所改变.

tensor.dot(tensor)     # torch 会转换成 [1,2,3,4].dot([1,2,3,4) = 30.0

# 变为
torch.dot(tensor.dot(tensor)

变量

什么是 Variable 

在 Torch 中的 Variable 就是一个存放会变化的值的地理位置. 里面的值会不停的变化. 就像一个裝鸡蛋的篮子, 鸡蛋数会不停变动. 那谁是里面的鸡蛋呢, 自然就是 Torch 的 Tensor 咯. 如果用一个 Variable 进行计算, 那返回的也是一个同类型的 Variable.

我们定义一个 Variable:

import torch
from torch.autograd import Variable # torch 中 Variable 模块

# 先生鸡蛋
tensor = torch.FloatTensor([[1,2],[3,4]])
# 把鸡蛋放到篮子里, requires_grad是参不参与误差反向传播, 要不要计算梯度
variable = Variable(tensor, requires_grad=True)

print(tensor)
"""
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable)
"""
Variable containing:
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

Variable 计算, 梯度 

我们再对比一下 tensor 的计算和 variable 的计算.

t_out = torch.mean(tensor*tensor)       # x^2
v_out = torch.mean(variable*variable)   # x^2
print(t_out)
print(v_out)    # 7.5

到目前为止, 我们看不出什么不同, 但是时刻记住, Variable 计算时, 它在背景幕布后面一步步默默地搭建着一个庞大的系统, 叫做计算图, computational graph. 这个图是用来干嘛的? 原来是将所有的计算步骤 (节点) 都连接起来, 最后进行误差反向传递的时候, 一次性将所有 variable 里面的修改幅度 (梯度) 都计算出来, 而 tensor 就没有这个能力啦.

v_out = torch.mean(variable*variable) 就是在计算图中添加的一个计算步骤, 计算误差反向传递的时候有他一份功劳, 我们就来举个例子:

v_out.backward()    # 模拟 v_out 的误差反向传递

# 下面两步看不懂没关系, 只要知道 Variable 是计算图的一部分, 可以用来传递误差就好.
# v_out = 1/4 * sum(variable*variable) 这是计算图中的 v_out 计算步骤
# 针对于 v_out 的梯度就是, d(v_out)/d(variable) = 1/4*2*variable = variable/2

print(variable.grad)    # 初始 Variable 的梯度
'''
 0.5000  1.0000
 1.5000  2.0000
'''

获取 Variable 里面的数据 ¶

直接print(variable)只会输出 Variable 形式的数据, 在很多时候是用不了的(比如想要用 plt 画图), 所以我们要转换一下, 将它变成 tensor 形式.

print(variable)     #  Variable 形式
"""
Variable containing:
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable.data)    # tensor 形式
"""
 1  2
 3  4
[torch.FloatTensor of size 2x2]
"""

print(variable.data.numpy())    # numpy 形式
"""
[[ 1.  2.]
 [ 3.  4.]]
"""

激励函数

在具体的例子中, 我们默认首选的激励函数是哪些. 在少量层结构中, 我们可以尝试很多种不同的激励函数. 在卷积神经网络 Convolutional neural networks 的卷积层中, 推荐的激励函数是 relu. 在循环神经网络中 recurrent neural networks, 推荐的是 tanh 或者是 relu (这个具体怎么选, 我会在以后循环神经网络的介绍中在详细讲解).

一句话概括 Activation: 就是让神经网络可以描述非线性问题的步骤, 是神经网络变得更强大. 如果还不是特别了解, 我有制作一个动画短片, 浅显易懂的阐述了激励函数的作用. 包懂.

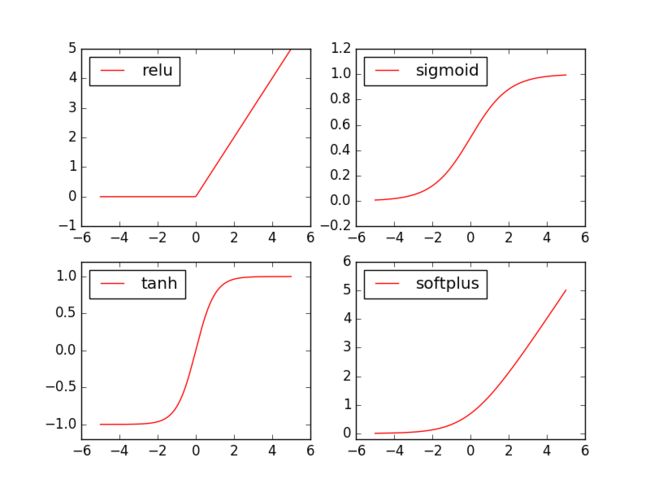
Torch 中的激励函数 

Torch 中的激励函数有很多, 不过我们平时要用到的就这几个. relu, sigmoid, tanh, softplus. 那我们就看看他们各自长什么样啦.

import torch
import torch.nn.functional as F     # 激励函数都在这
from torch.autograd import Variable

# 做一些假数据来观看图像
x = torch.linspace(-5, 5, 200)  # x data (tensor), shape=(100, 1)
x = Variable(x)

接着就是做生成不同的激励函数数据:

x_np = x.data.numpy()   # 换成 numpy array, 出图时用

# 几种常用的 激励函数
y_relu = F.relu(x).data.numpy()
y_sigmoid = F.sigmoid(x).data.numpy()
y_tanh = F.tanh(x).data.numpy()
y_softplus = F.softplus(x).data.numpy()
# y_softmax = F.softmax(x)  softmax 比较特殊, 不能直接显示, 不过他是关于概率的, 用于分类

接着我们开始画图, 画图的代码也在下面:

import matplotlib.pyplot as plt  # python 的可视化模块, 我有教程 (https://morvanzhou.github.io/tutorials/data-manipulation/plt/)

plt.figure(1, figsize=(8, 6))
plt.subplot(221)
plt.plot(x_np, y_relu, c='red', label='relu')
plt.ylim((-1, 5))
plt.legend(loc='best')

plt.subplot(222)
plt.plot(x_np, y_sigmoid, c='red', label='sigmoid')
plt.ylim((-0.2, 1.2))
plt.legend(loc='best')

plt.subplot(223)
plt.plot(x_np, y_tanh, c='red', label='tanh')
plt.ylim((-1.2, 1.2))
plt.legend(loc='best')

plt.subplot(224)
plt.plot(x_np, y_softplus, c='red', label='softplus')
plt.ylim((-0.2, 6))
plt.legend(loc='best')

plt.show()

 

关系拟合（回归）

 

我会这次会来见证神经网络是如何通过简单的形式将一群数据用一条线条来表示. 或者说, 是如何在数据当中找到他们的关系, 然后用神经网络模型来建立一个可以代表他们关系的线条.

建立数据集 

我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y数据加上一点噪声来更加真实的展示它.

import torch
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())                 # noisy y data (tensor), shape=(100, 1)

# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()

建立神经网络 

建立一个神经网络我们可以直接运用 torch 中的体系. 先定义所有的层属性(__init__()), 然后再一层层搭建(forward(x))层于层的关系链接. 建立关系的时候, 我们会用到激励函数, 如果还不清楚激励函数用途的同学, 这里有非常好的一篇动画教程.

import torch
import torch.nn.functional as F     # 激励函数都在这

class Net(torch.nn.Module):  # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()     # 继承 __init__ 功能
        # 定义每层用什么样的形式
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.predict = torch.nn.Linear(n_hidden, n_output)   # 输出层线性输出

    def forward(self, x):   # 这同时也是 Module 中的 forward 功能
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.predict(x)             # 输出值
        return x

net = Net(n_feature=1, n_hidden=10, n_output=1)

print(net)  # net 的结构
"""
Net (
  (hidden): Linear (1 -> 10)
  (predict): Linear (10 -> 1)
)
"""

训练网络 

训练的步骤很简单, 如下:

# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)  # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss()      # 预测值和真实值的误差计算公式 (均方差)

for t in range(100):
    prediction = net(x)     # 喂给 net 训练数据 x, 输出预测值

    loss = loss_func(prediction, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward()         # 误差反向传播, 计算参数更新值
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

可视化训练过程 

为了可视化整个训练的过程, 更好的理解是如何训练, 我们如下操作:

import matplotlib.pyplot as plt

plt.ion()   # 画图
plt.show()

for t in range(200):

    ...
    loss.backward()
    optimizer.step()

    # 接着上面来
    if t % 5 == 0:
        # plot and show learning process
        plt.cla()
        plt.scatter(x.data.numpy(), y.data.numpy())
        plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(), fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)