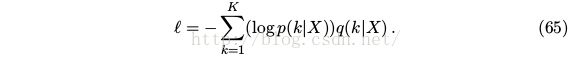[深度学习论文笔记][Image Classification] Rethinking the Inception Architecture for Computer Vision
1 General Design Principles
[Avoid Representational Bottlenecks, Especially Early in the Network] The representation (feature map) size should gently decrease from the inputs to the outputs before reaching the final representation used for the task at hand. The dimensionality merely provides a rough estimate of information content since it discards important factors like correlation structure.
[Higher Dimensional Representations are Easier to Process Locally Within a Network] Increasing the activations per tile in a convolutional network allows for more disentangled features. The resulting networks will train faster.
[Spatial Aggregation Can Be Done Over Lower Dimensional Embeddings Without Much or Any Loss in Representational Power] One can reduce the dimension of the input representation before the spatial aggregation (e.g. 3 × 3 convolution).
[Balance the Width and Depth of the Network] The optimal improvement for a constant amount of computation can be reached if both are increased in parallel.
2 Factorizing Convolutions with Large Filter Size
[Factorization Into Smaller Convolutions] Replace 5 × 5 conv by two 3 × 3 conv. Replace the first 7 × 7 conv by a sequence of 3 × 3 conv.
[Spatial Factorization into Asymmetric Convolutions] Replace 3 × 3 conv by a 3 × 1 conv followed by a 1 × 3 conv.
• This factorization does not work well on early layers.
• But it gives very good results on medium grid-sizes (On 12 × 12 to 20 × 20 feature maps.
3 Utility of Auxiliary Classifiers
• Auxiliary classifiers did not result in improved convergence early in the training.
• Near the end of training, the network with the auxiliary branches starts to overtake the accuracy of the network without any auxiliary branch and reaches a slightly higher plateau.
• The removal of the lower auxiliary branch did not have any adverse effect on the final quality of the network.
• The main classifier of the network performs better if the side branch is batch-normalized or has a dropout layer.
4 Efficient Grid Size Reduction
Say we want to double the number of channels and half the spatial dimensions, i.e., D × H × W → 2D × H/2 × W/2 .
[Traditional Ways] Method 1
• D × H × W → conv → 2D × H × W → pool → 2D × H/2 × W/2 .
• # multiplications: 2D × H × W × 1 × 1 × D = 2D^2HW .
Method 2
• D × H × W → pool → D × H/2 × W/2 → conv → 2D × H/2 × W/2 .
• # multiplications: 2D × H/2 × W/2 × 1 × 1 × D = 1/2 D^2HW .
• But this creates a representational bottlenecks.
[Inception Way] See Fig. It is both cheap and avoids the representational bottleneck.
![[深度学习论文笔记][Image Classification] Rethinking the Inception Architecture for Computer Vision_第1张图片](http://img.e-com-net.com/image/info8/ea09a4ecbd1a404ca36e6e2e2223196c.jpg)
5 Model Regularization via Label Smoothing
For each X, the model computes the probability of each label k
Loss:
Where q(k|X) is the ground-truth distribution.
[Traditional]
• It may result in overfitting: If the model learns to assign full probability to the ground-truth label for each training example, it is not guaranteed to generalize.
• It encourages the differences between the largest logit and all others to become large,this, which reduces the ability of the model to adapt.
[Label Smoothing Regularization]
Replace q(k|X) with
• In practice, set ε = 0.1 .
• This has an improvement of about 0.2% both for top-1 and top-5 error.
6 Training Details
RMSProp with 0.9
• Batch size 32.
• Training 100 epochs.
• Base learning rate 0.045.
• Decayed every 2 epoch using an exponential rate of 0.94.
• Gradient clipping with threshold 2.0 to stabilize the training.
7 Performance on Lower Resolution Input
Reduce the strides of the first two layer in the case of lower resolution input, or by simply removing the first pooling layer of the network.
8 Results
ILSVRC-2012, for top-5 error
• 1 CNN: 5.64%.
• 5 CNNs: 3.58%.