几种常见的Graph Embedding方法

图（Graph）是一个常见的数据结构，现实世界中有很多很多任务可以抽象成图问题，比如社交网络，蛋白体结构，交通路网数据，以及很火的知识图谱等，甚至规则网络结构数据（如图像，视频等）也是图数据的一种特殊形式。针对graph的研究可以分成三类：1.简单的graph算法：如生成树算法，最短路算法，复杂一点的二分图匹配，费用流问题等等；2.概率图模型：将条件概率表达为图结构，并进一步挖掘，典型的有条件随机场等；3.图神经网络：研究图结构数据挖掘的问题，典型的有graph embedding，graph CNN等。

总览

在介绍Graph Embedding之前，我们先回顾什么是Embedding？Embedding在数学上是一个函数，将一个空间的点映射到另一个空间，通常是从高维抽象的空间映射到低维的具象空间。Embeding的意义将高维数据转换到低维利于算法的处理；同时解决one-hot向量长度随样本的变化而变化，以及无法表示两个实体之间的相关性这一问题。

最常见的embeding方法是word2vec，根据语料库中单词的共现关系求出每个单词的embedding，常用的word2vec模型有cbow和skip-gram两种，cbow根据上下文预测中心词，skip-gram根据中心词预测上下文(详见word2vec 中的数学原理详解)。因此既然自然语言中的单词可以通过共现关系进行embedding，那么将graph类比成整个语料库，图中的节点类比成单词，我们是否也可以通过共现关系对graph中的node进行embedding？对于word2vec而言，语料库中的每个句子都可以描述单词之间的共现，对于graph，这种共现关系如何描述呢？接下来我们将对多种不同的graph embedding方式进行展开。

Graph Embedding

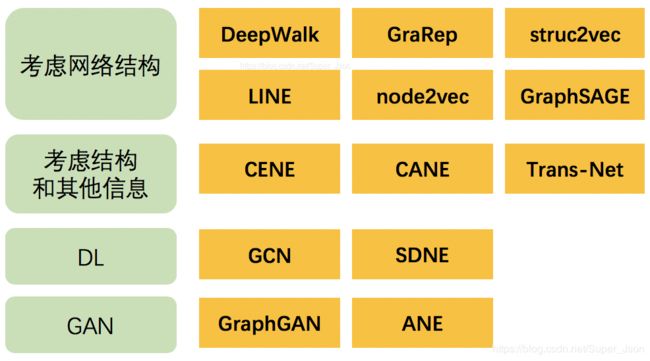
Graph Embedding 的中心思想就是找到一种映射函数，该函数将网络中的每个节点转换为低维度的潜在表示。利于计算存储，不用再手动提特征（自适应性），下图是graph embeding的几种常见分类

DeepWalk

DeepWalk 通过将节点视为单词并生成短随机游走作为句子来弥补网络嵌入和单词嵌入之间的差距。然后，可以将诸如 Skip-gram 之类的神经语言模型应用于这些随机游走以获得网络嵌入。其优点是首先其可以按需生成随机游走。由于 Skip-gram 模型也针对每个样本进行了优化，因此随机游走和 Skip-gram 的组合使 DeepWalk 成为在线算法。其次，DeepWalk 是可扩展的，生成随机游走和优化 Skip-gram 模型的过程都是高效且平凡的并行化。最重要的是，DeepWalk 引入了深度学习图形的范例。

  用SkipGram的方法进行网络中节点的表示学习。那么，根据SkipGram的思路，最重要的就是定义Context，也就是Neighborhood。​NLP中，Neighborhood是当前Word周围的字，本文用随机游走得到Graph或者Network中节点的Neighborhood。

（1）随机游走随机均匀地选取网络节点，并生成固定长度的随机游走序列，将此序列类比为自然语言中的句子（节点序列=句子，序列中的节点=句子中的单词），应用skip-gram模型学习节点的分布式表示，skip-gram模型详见：http://blog.csdn.net/u013527419/article/details/74129996
（2）前提：如果一个网络的节点服从幂律分布，那么节点在随机游走序列中的出现次数也服从幂律分布，并且实证发现NLP中单词的出现频率也服从幂律分布。

Network/graph ---------random walk ---------得到节点序列（representation mapping）-------- 放到skip-gram模型中（中间节点预测上下        文节点）--------- output：representation

node2vec

node2vec在DW的基础上，定义了一个bias random walk的策略生成序列，仍然用skip gram去训练。

论文分析了BFS和DFS两种游走方式，保留的网络结构信息是不一样的。 DeepWalk中根据边的权重进行随机游走，而node2vec加了一个权重调整参数α：t是上一个节点，v是最新节点，x是候选下一个节点。d(t,x)是t到候选节点的最小跳数。 通过不同的p和q参数设置，来达到保留不同信息的目的。当p和q都是1.0的时候，它等价于DeepWalk。

这篇文章来自于Jure Leskovec的组。文章所提出的方法软件实现。

文章的主要想法就是，利用SkipGram的方法，来为Networks抽取Representation。那么，自然，根据SkipGram的思路，最重要的就是定义这个Context，或者说是Neighborhood。​从文本的角度来说，这个Neighborhood当然就是当前Word周围的字，这个定义非常自然。但是对于Graph或者Network来说就来得没那么容易了。

文章阐述了一般所采用Depth-First Search或者是Breadth-First Search来Sample一个Node的周边Node的问题。简单来说，BFS比较容易有一个Microscopic的View而DFS容易有一个Macro-view，两者都有Representative的问题。

文章的核心思想是采用Random Walk来代替DFS或者BFS。文章定义了一种二阶的Random Walk，拥有两个参数，来控制多大的概率反复经过一些Node和控制所谓的Inward和Outward。总之，整个Random Walk的目的就是在DFS和BFS之间采取某种平衡。

文章虽然提出的是关于Node Feature提取的算法，但是Edge Feature也可以很容易从Node Feature导出。

总体感觉是，硬要用SkipGram或者WordVec的想法在Networks上做，还显得比较牵强。因为有这个Neighborhood的概念，在Graph上，反而不是那么直观得定义，因此所有类似的工作都显得比较别扭。当然，这篇文章也不失为一种不错的Heuristic。​​​​​

具体应用可以参考腾讯lookalike算法。

LINE

（1）先区分两个概念：

一阶相似度：直接相连节点间，例如6与7。

定义节点vi和vj间的联合概率为

v代表节点，u代表节点的embedding。上面式子的意思是两节点越相似，內积越大，sigmoid映射后的值越大，也就是这两节点相连的权重越大，也就是这两个节点间出现的概率越大？？？。

 

二阶相似度：通过其他中介节点相连的节点间例如5与6。

用的是一个条件概率

 

（2）目标是让NRL前后节点间相似度不变，也节点表示学习前如果两个节点比较相似，那么embedding后的这两个节点表示向量也要很相似。--此文中用的是KL散度，度量两个概率分布之间的距离。KL散度的相关知识详见：http://blog.csdn.net/u013527419/article/details/51776786

以保证其一阶相似度为例子：

embedding前：节点vi和vj间的经验联合概率为

所以，最小化：

 

 

前面说了很多GE的模型，从古典方法，到只考虑结构的模型，再到考虑节点和变extra info的模型，再到深度模型，大家可能觉眼花缭乱，并不知道实际中应该用哪个模型。

这里我提一句，你选择的模型一定要和你的实际问题相关：

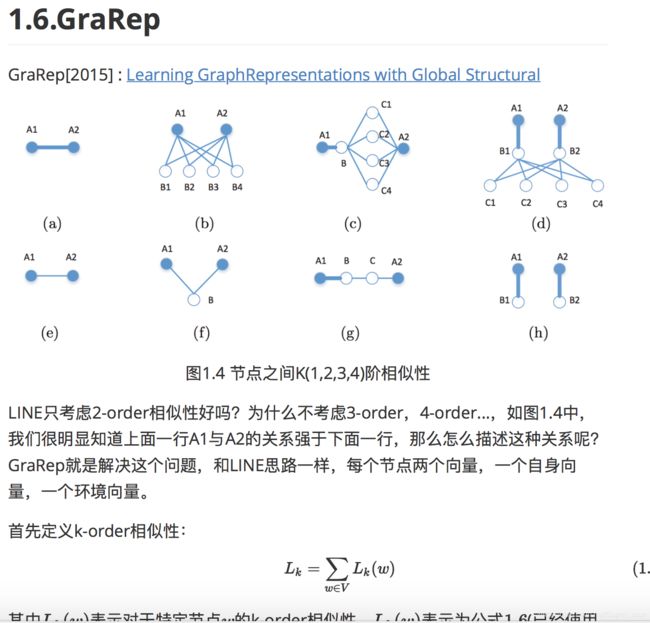
1.比如你的问题更加关注内容相似性（局部邻域相似性）那么你可以选择node2vec，LINE，GraRep等；

2.如果你的问题更加关注结构相似性，你可以选择struc2vec，这里可以简单说以下为什么蚂蚁金服风控模型使用struc2vec相比node2vec有质的提升，这是因为在风控领域，你可信并不能代表你的邻居可信（有些“大 V”节点的邻居众多），但是一个直观的感觉是，如果两个人在图中处于相似的地位（比如两个“大 V”），那么这两个人应该都可信或都不可信，并且一般来说这样两个人（节点）相距较远；

3.再者如果你的模型需要考虑节点和边的额外信息，那么你可选择CANE，CENE，Trans-net等；

4.如果你想处理大规模易变图，你可以采用GraphSAGE，或者先使用其他GE方法，再使用GraphSAGE归纳学习；

如果你想微调你的模型，你可选择GraphGAN；

甚至你可以选择很多GE方法，并将得到的embedding向量进行聚合，比如concat等方式；