MATLAB | 经典力学框架下的三体运动数值模拟软件

概要： 这是我大三上学期某一门课程的一次作业。本文基于MATLAB及其GUI界面设计了一个基于经典力学的三体运动数值模拟软件，旨在建立经典力学框架内的空间三质点运动模型，又名为三体运动模型。软件根据当前的质点初始运动参数，运用数值模拟，迭代计算出后续每一时刻各个质点的运动参数，并将计算结果实时显示出来。本软件可用于质点力学与基础天体物理学的自主学习、教学演示和相关领域的科学研究。
关键字： MATLAB;三体运动;数值模拟;可视化
 

1 背景说明

   公元1900年，在二十世纪第一次数学家大会上，数学家希尔伯特第一次提出了“完美数学问题”准则：问题既能被简明扼要地表达出来，然而问题的解决又是如此困难以至于必须要有全新的思想方法才能解决。为了说明他的观点，希尔伯特举了两个最经典的例子，第一是费马猜想，第二就是N体问题。

   N题问题是指：三维自由空间中N个可视为质点的恒质天体在某一时间断面质量、位置及初始速度已知的条件下求该时刻后任一时刻N个质点的位置和速度。当N小于3时，该问题可以用牛顿力学完美解决，但当N大于等于3后，仅仅依靠经典力学体系无法求得精确解。

   三体问题的起源最晚可追溯到17世纪，当牛顿的划时代巨著《自然哲学的数学原理》问世之后，他的引力理论已经能正确预测两个天体（如一颗恒星和一颗行星）的运动规律，即两个互相吸引的天体的轨道为椭圆形。但是，三个天体的问题要复杂得多，在当时，牛顿没能提出类似的通解。时光流逝，经过18、19两个多世纪几代数学家的研究，人们已经认识到三体系统是一个混沌系统，不存在解析解。混沌系统是典型的非线性系统，它的重要特征之一在于误差的累积性，且误差来源于计算本身——这个“计算本身”是指计算数据的无理性以及混沌系统的微扰敏感性。也就是说，三体系统不仅不具备普遍意义上的解析解，甚至连较长期的数值预测也无法实现，这也是三体问题吸引和困扰几代最杰出的数学家几百年之久的重要原因。

   以上所述就是开展本实验的大致背景，本实验拟在经典力学体系框架内，运用迭代算法对三体运动模型进行数值模拟。正如上文所说，三体系统的无解析解性和误差累积性决定了“经典力学+数值模拟”的办法仅能在宏观视角粗糙地展现三体运动特征，且预测结果的可信度将随时间的增加而下降。所幸的是，三体系统作为一个混沌系统，也有若干特殊的解可以解析表达。迄今为止，科学家们总共发现了16族三体问题的特解，其中包含有若干稳定的解析解。在这其中，塞尔维亚物理学家Milovan Šuvakov和V. Dmitrašinović于2012年前后采用数值模拟的思路，在已有特解的基础上，通过对各项初始值进行微调，利用计算机上进行了海量运算，终于寻找得到13族特解，一举超过了过去三百多年间所找到的所有特解的总和。这一振奋人心的科学发现不仅拓宽了在三体问题上人类已有的知识界限，更提出了一种在混沌中求解析解的计算方法。两位科学家的研究论文Three Classes of Newtonian Three-Body Planar Periodic Orbits已于2013年3月发表在知名物理学杂志《PHYSICAL REVIEW LETTERS》上。

2 实验目的

   本实验基于计算机数值模拟思路，利用迭代法，在经典力学体系框架内建立三体运动模型并完成多种特解的可视化实现。

3 基本原理及思路

   设三维自由空间中有三个质量、初始位置和初始速度已知的三个质点，分别记作：

A(M1,X1,Y1,Z1,U1,V1,W1); B(M2,X2,Y2,Z2,U2,V2,W2); C(M3,X3,Y3,Z3,U3,V3,W3);

 
其中，X、Y、Z分别表示各个质点在X、Y、Z方向上的坐标，U、V、W分别表示各个质点在X、Y、Z方向上的速度分量。

   设fAB表示质点A对质点B的作用力，fBA表示质点B对质点A的反作用力，则三个质点之间的万有引力可表示为f12、f23、f31、f31、f32、f21，根据牛顿第三定律，有：

f12=-f21; f23=-f32; f31=-f13;

 
这样，牛顿第三定律将力的变量由6个减少到3个。

   根据牛顿第二定律，质点间相互作用力f12、f23、f31可分别被表达为：

f12=g*M1*M2/R12^3*[X1-X2,Y1-Y2,Z1-Z2]; f23=g*M2*M3/R23^3*[X2-X3,Y2-Y3,Z2-Z3]; f31=g*M3*M1/R13^3*[X3-X1,Y3-Y1,Z3-Z1];

 
其中g是引力常量，取值为6.67x10^-11(N·m2 /kg^2)，R12、R23、R13分别表示两两质点之间的距离，可以表达为：

R12=sqrt((X1-X2)^2+(Y1-Y2)^2+(Z1-Z2)^2); R13=sqrt((X1-X3)^2+(Y1-Y3)^2+(Z1-Z3)^2); R23=sqrt((X2-X3)^2+(Y2-Y3)^2+(Z2-Z3)^2);

 
注意，式中f12、f23、f31表达为三维矢量。

   由于三体问题是一个发生在三维自由空间的动力学问题，所以势必要进行矢量分析。本实验建立空间直角坐标系，根据矢量的叠加性原理，将所有三维矢量包括引力、加速度、速度和位置矢量等分别分解到X、Y、Z三个坐标轴上分析，就将矢量运算简化为标量运算。现在，以X轴为例，对三体系统进行经典动力学分析。

   设三质点在X轴上的加速度分别为Ax1、Ax2、Ax3，则可以表达为：

Ax1=(-f12(1)+f31(1))/M1; Ax2=( f12(1)-f23(1))/M2; Ax3=( f23(1)-f31(1))/M3;

   速度可以表达为：

U1=U1+Ax1*t; U2=U2+Ax2*t; U3=U3+Ax3*t;

   位置矢量可以表达为：

X1=X1+U1*t+1/2*Ax1*t^2; X2=X2+U2*t+1/2*Ax2*t^2; X3=X3+U3*t+1/2*Ax3*t^2;

 
其中f12(1)意为三维矢量f12在X轴向上的分量，t为迭代的时间间隔，本实验中t的取值为0.00001。

   以此类推，在Y轴和Z轴上也进行类似的分析和计算，就可以在三维自由空间中建立一个简单的三体运动模型。

4 成果展示

4.1 用户界面展示

   为了完成三体运动模型的可视化实现，在试验中采取了MATLAB的GUI界面设计，形成了较为完备和友好的软件交互界面。GUI界面如图1和图2所示：

图1 GUI控制界面(1)

 
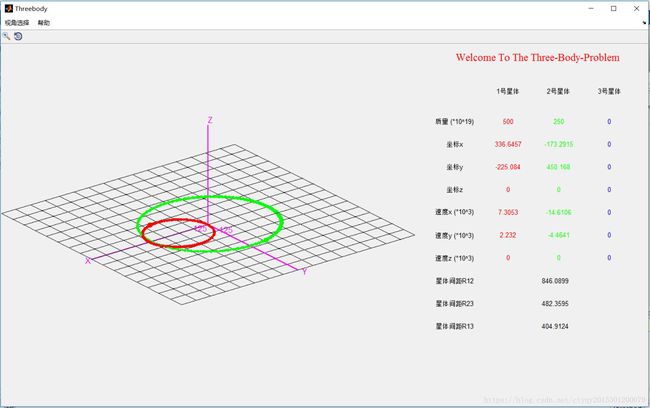
   其中左侧为图形显示界面，右侧为数据显示界面。左侧显示各质点的运动轨迹，右侧显示个质点的质量、坐标、速度和相互距离等信息。

   在界面空白处点击鼠标右键，出现如图2所示的设置界面：

图2 GUI控制界面(2)

 
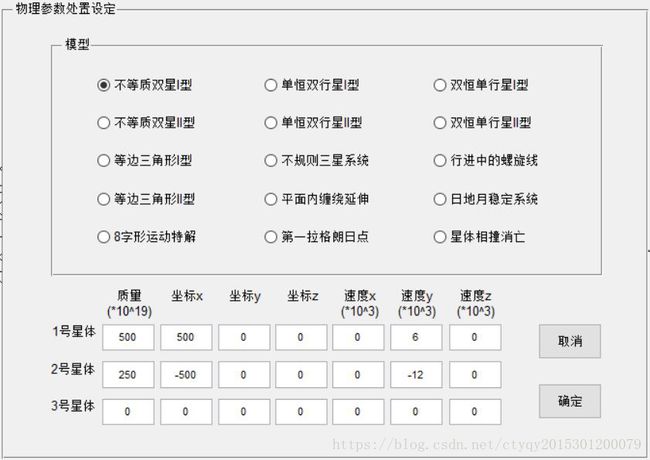
   该界面中，上侧为15种可选模型，代表了15种确定的初始条件；下侧为各模型的初始参数值。用户选择其中一种模型，按下“确定”按钮即可完成设置。同时，用户也可以直接修改下侧显示方框内的数据，随意设置初始参数，软件也将按照用户所设置的值运行。

   软件设置了两个菜单和两个工具，如图3所示：

图3 软件菜单栏与设置栏

 
   在“视角选择”菜单中，用户有4种视角可以选择：标准视角、XOY视角、YOZ视角、ZOX视角；在“帮助”中，用户可以了解到软件的版本信息和使用指导；第一个工具可以调整视距远近，第二个工具可以改变视角。上述菜单中的各个子项都有快捷键与之一一对应。

4.2 所需文件

   运行本软件需要3个文件：源文件、数据包和一个音乐提示文件，如图4所示：

图4 软件运行所需文件

 
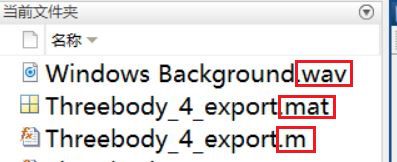
   其中，.m文件是源代码文件，.mat文件是数据包，.wav是一段音频，当星体相碰撞时播出用作提示。

4.3 软件运行效果

   随着用户对各星体初始参数的改变，软件的运行效果有无限种可能，本节将对它们进行展示和分析。

4.3.1 不等质双星

   在这种情况下，两个质量不等的星体互相缠绕旋转。这是一个双体运动，由万有引力定律我们很容易得到双体运动的确定解。当两质点质量相差不大且可以形成稳定系统时，双体各自围绕其公共质心运动，公共质心始终处于两质点各自轨道的公共焦点处。当两质点质量相差悬殊且可以形成稳定系统时，可以近似认为质量大的质点静止于质量小者运动轨迹之焦点附近。一定条件下，双体可以形成特殊双星系统，即两质点围绕共同的圆心做匀速圆周运动，此时两质点角速度之值相等。实验产生的双体运动效果如图5与图6所示。

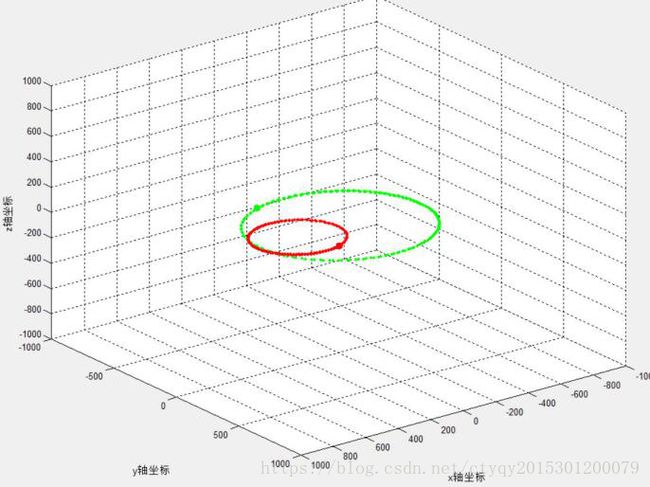图5 不等质量双星I型轨迹（1）

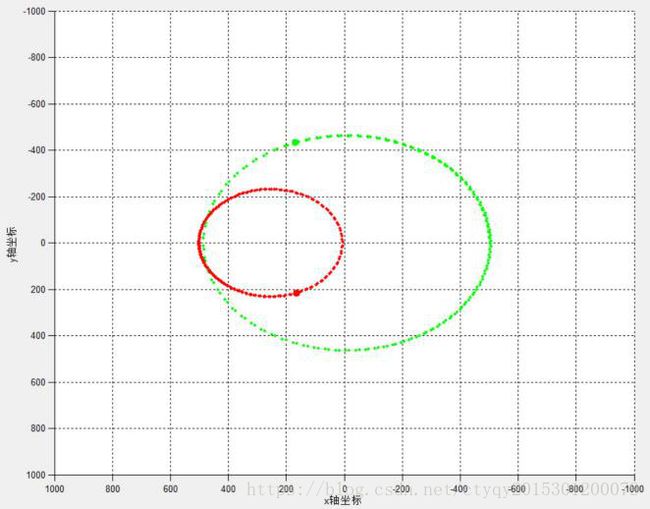图5 不等质量双星I型轨迹（2）

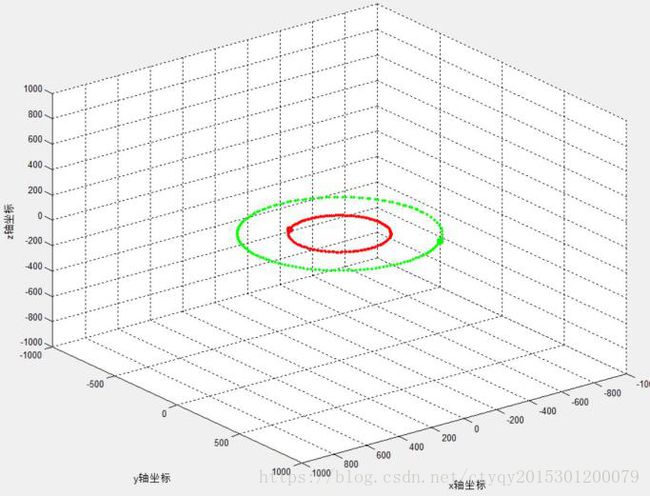图6 不等质量双星II型轨迹（1）

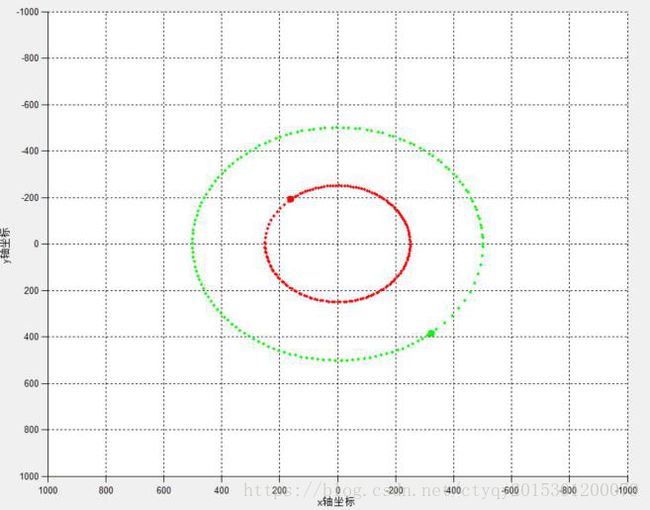图6 不等质量双星II型轨迹（2）

   质量之比皆为2：1的两质点拥有不同的初速度，形成了有明显差异的运动轨迹。

4.3.2 近似等边三角形

   这种情况下，三质点围绕着共同的质心在同一平面内运动，且三质点所构图形始终为等边三角形，公共质心相对于三质点始终保持静止。图7所示为其中两种情况。

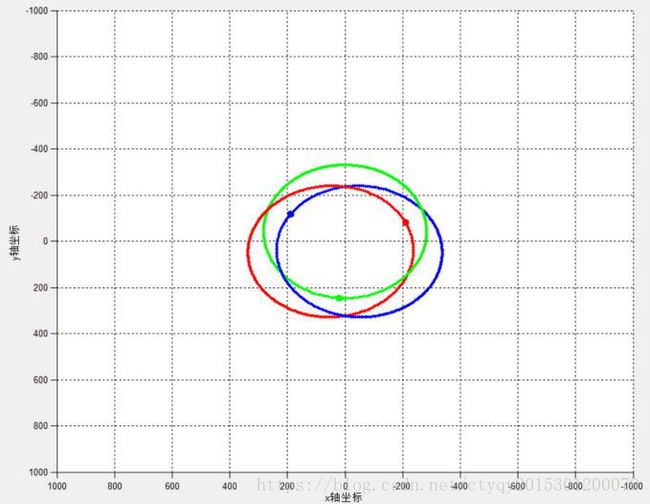图7 近似等边三角形运动轨迹（1）

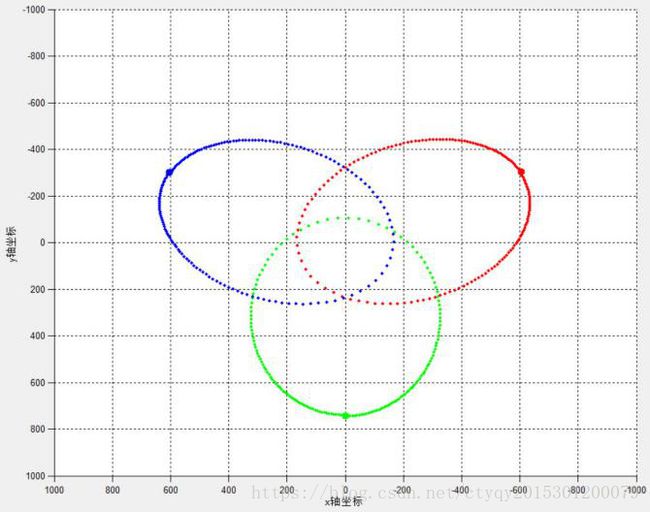图7 近似等边三角形运动轨迹（2）

   等质量、等初速度的各质点的运动轨迹都是椭圆，但是偏心率有明显差异，区别点在于初始位置以及初始速度大小。在特殊情况下可以形成三星三等分标准圆周并围绕圆心做匀速圆周运动的情形。

4.3.3 单恒星双行星型

   在这种情况下，三质点中有一个质点的质量远大于其余两质点，而质量小的两质点质量相仿。这种模型在宇宙中比较常见，例如太阳与火星、地球的关系。实验产生的单恒星双行星型三体运动效果如图8与图9所示。

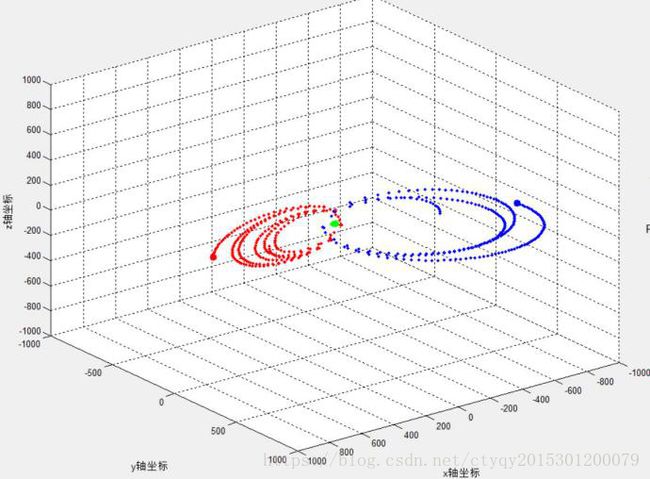图8 单恒星双行星I型运动轨迹（1）

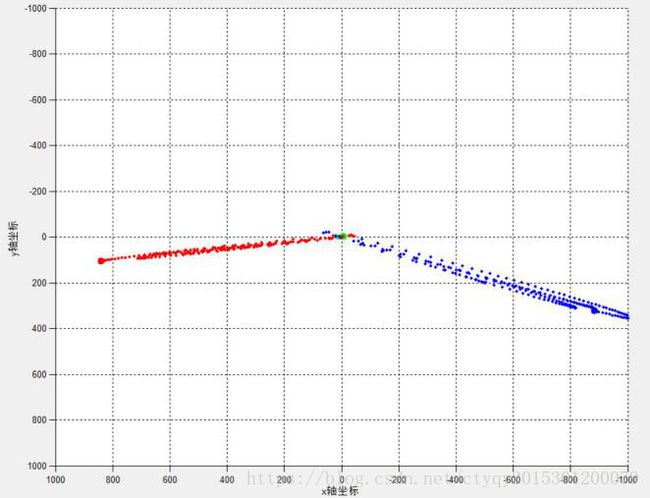图8 单恒星双行星I型运动轨迹（2）

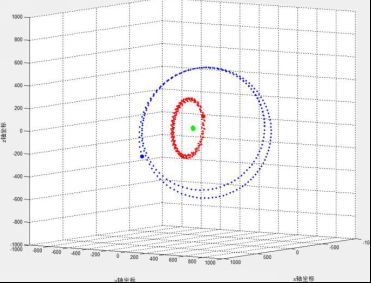图9 单恒星双行星II型运动轨迹（1）

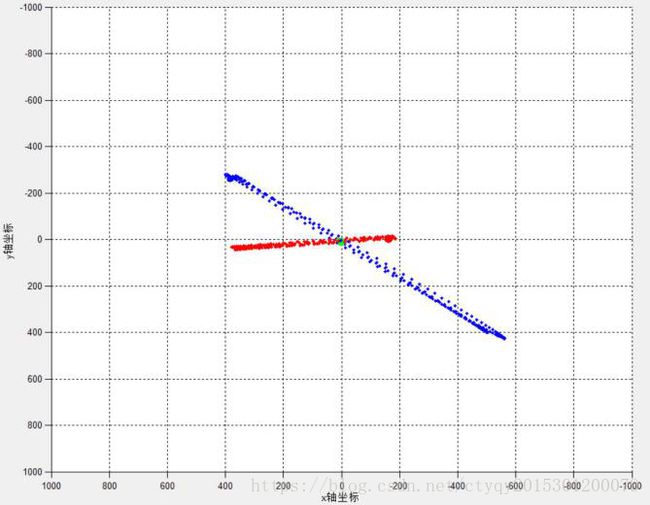图9 单恒星双行星II型运动轨迹（2）

   上述两种情况的共性在于基本都是两小质量质点围绕大质量质点运动，且各自与大质量质点基本保持在一个平面内。两轨道面夹角清晰可见。不同之处在于，I型两小质量质点的运动轨迹偏心率较大，轨道有相交处，且离心倾向明显。在实验中，I型模型运行一段时间后将崩溃，三星分离不再相聚；而二型系统却可以维系很长一段时间。很显然，II型系统模型更接近于太阳系中太阳与近地行星的运动状态。

4.3.4 双恒星单行星型

   在这种情况下，三质点中有两个质点的质量远大于第三个质点，而质量大的两质点质量相仿。实际上，双星系统在宇宙中极为常见，双星系统及其行星之间的关系就符合本模型所模拟的情形。实验产生的双恒星单行星模型三体运动效果如图10、图11和图12所示。

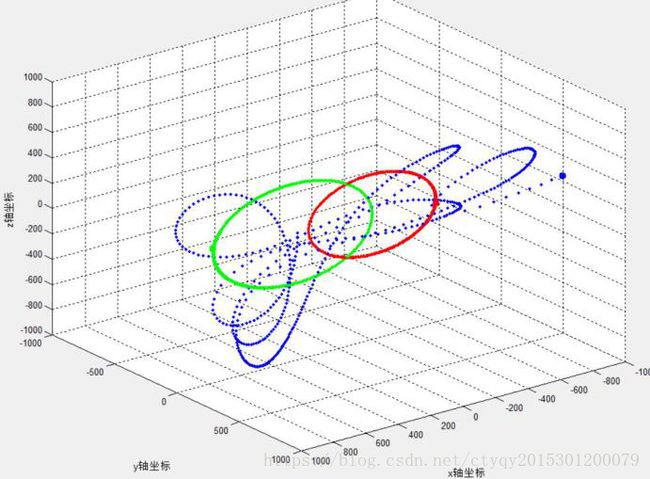图10 双恒星单行星I型运动轨迹（1）

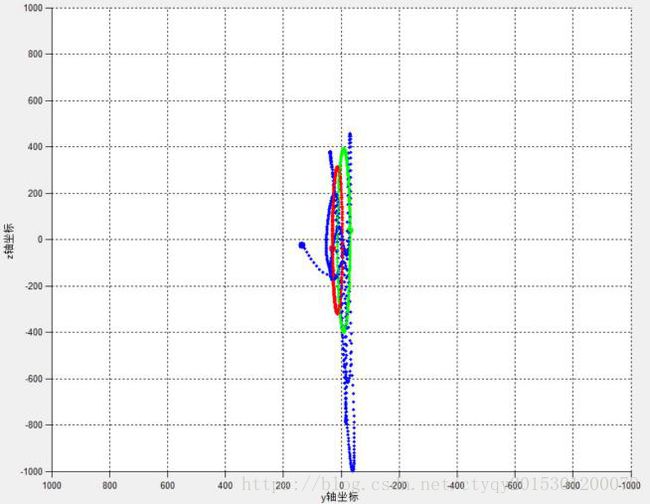图10 双恒星单行星I型运动轨迹（2）

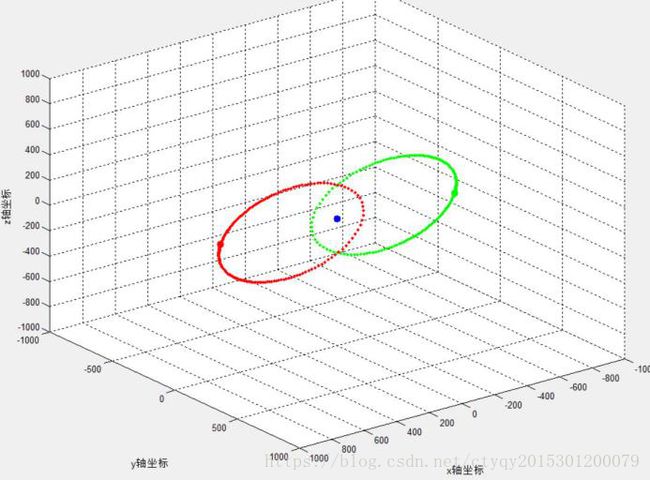图11 双恒星单行星II型运动轨迹（1）

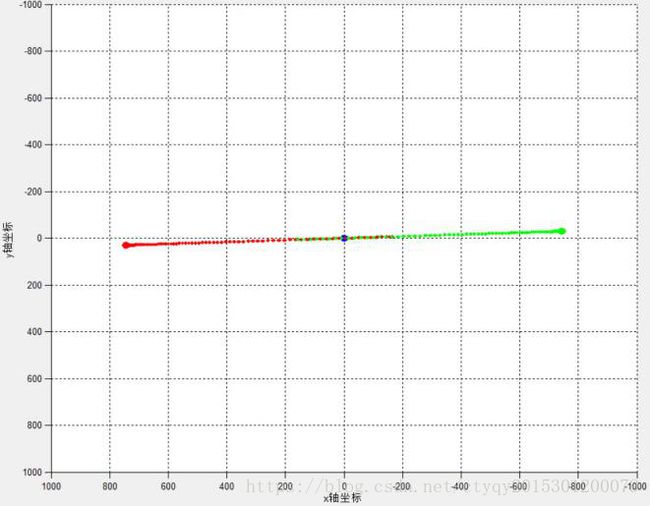图11 双恒星单行星II型运动轨迹（2）

   首先看双恒星单行星I型，显然，红绿两色质点为大质量质点，蓝色质点处于红绿质点引力场内。由于质量的不对等，导致了大质量质点能轻易影响小质量质点而小质量质点难以撼动大质量质点。这种模型的前途只有两种：要么小质量质点被大质量质点甩出模型外，从而三体模型变为稳定的双体模型，要么小质量质点与大质量质点相撞。在天文学中，星体相撞又有多种可能的结局，其中最极端的两种可能包括行星（小质量质点）融入恒星（大质量质点）从而构成双星系统，以及行星将恒星撞至失去结构，留下一片星骸和剩余的一颗恒星。

   双恒星单行星II型是一种极其理想化的情况，即行星位于恒星运动轨迹交集区域的正中央，即两恒星轨迹的公共焦点处，且两恒星等质量，这就构成了一个不稳定解析解。需要注意的是，这个解是极其脆弱的，只要对中央行星造成一丝一毫的扰动，它将立马“跌下神坛”，转变成双恒星单行星I型的情况。同样的，这种理想化模型也适用于单恒星双行星系统；更进一步，只要三体中有两质点等质量，在合适的初始条件下就可以构建出这样的模型。

图12 行进中的螺旋线（1）

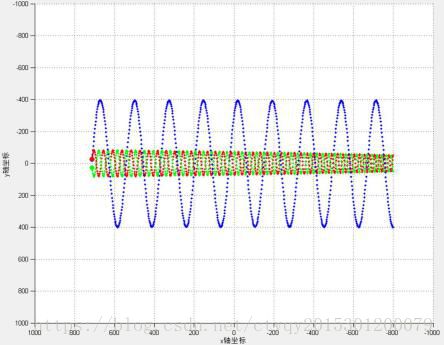图12 行进中的螺旋线（2）

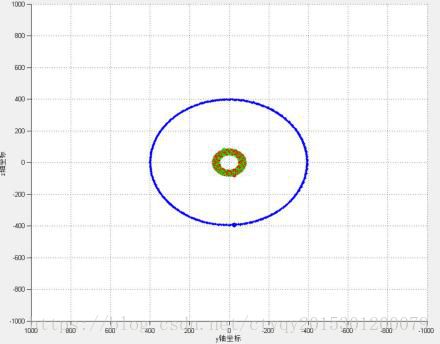图12 行进中的螺旋线（3）

   再看图12所示情形，GUI中对这一初始条件的命名为“行进中的螺旋线”，它实质上也是双恒星单行星模型中的一种。两颗距离相近的恒星（大质量质点）形成双体，绕公共质点匀速圆周运动，一颗行星（小质量质点）在较远处绕两颗恒星的公共质心匀速圆周运动，同时，这三颗星具有垂直于轨道面的相同速度，就构成了这一模型。从截面看，三体绕公共圆心做匀速圆周运动。需要注意的是，只有当恒星、行星质量相差非常大以及行星离恒星较远时才能构建出这样能稳定一段时间的系统（因为在计算引力时使用了近似，舍去了二阶无穷小量）。即使满足上述条件，由于受到行星持之以恒的引力作用，两恒星间距会逐渐加大，如图9中间小图所示。恒星间距持续扩大，直到行星被其中一颗恒星捕获，又变成图7中双恒星单行星I型的情况。

   结合已有观测资料，宇宙中虽然存在着大量双恒星系统，但是却极少能发现带有行星的双星。上述分析也与之吻合，所有特殊情况终将变为一般情况，行星将面临逃离和坠毁两种命运，很难在双星系统中长时间生存。

4.3.5 三体在平面内缠绕延伸

   这种情况下三质点将在同一平面内沿同一方向互相缠绕、整体延伸。这也可以认为是单恒星双行星的一个例子，基本状况是分布于两侧的行星（小质量质点）轮流靠近恒星（大质量质点），从而在某种程度上维持了彼此的平衡。但是，混沌系统中任一微小误差都将在后续运行中叠加，所以这种模型完全是人为设计产生的，在自然界中基本不存在。即使存在，也只能维持相当短的时间。实验产生的三体在平面内缠绕延伸运动效果如图13所示。

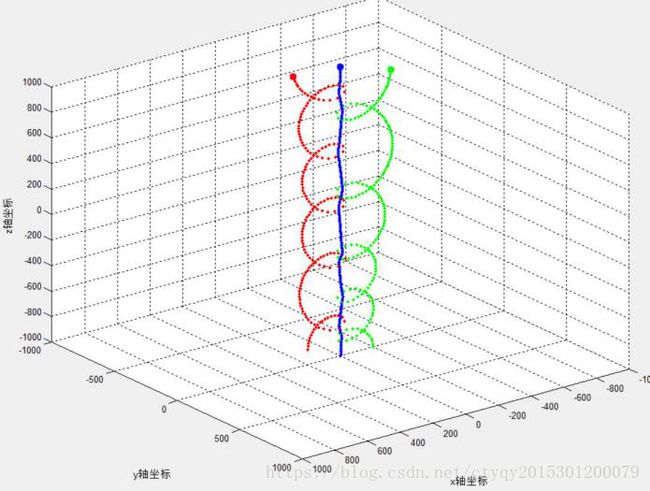图13 三体在平面内缠绕延伸（1）

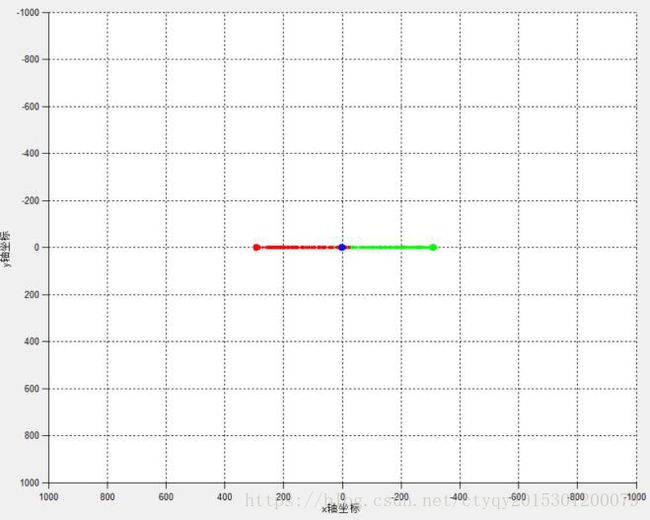图13 三体在平面内缠绕延伸（2）

4.3.6 日地月稳定系统

   这种情况下，三质点质量互相相差较大，月球（小质量质点）绕地球（中等质量质点）旋转，地球绕太阳（大质量质点）旋转，且日地轨道与地月轨道间产生轨道夹角，即月球并不一直处于日地轨道平面。另一方面，若以太阳为视角，地球围绕太阳沿椭圆轨道旋转，而月球围绕太阳做螺旋运动。实验产生的日地月稳定系统运动效果如图14所示。

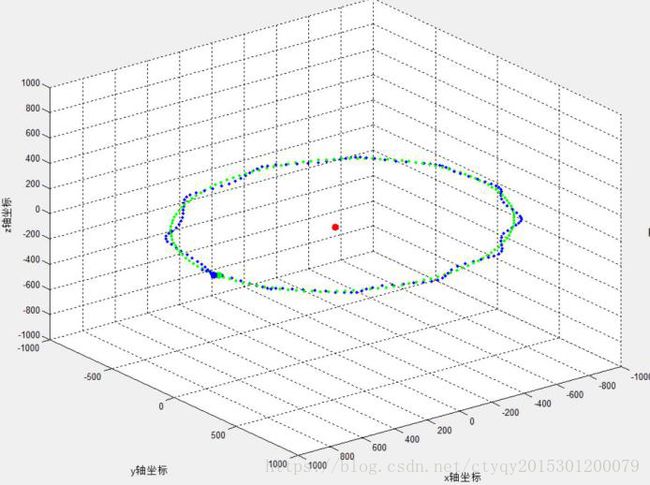图14 日地月系统模型（1）

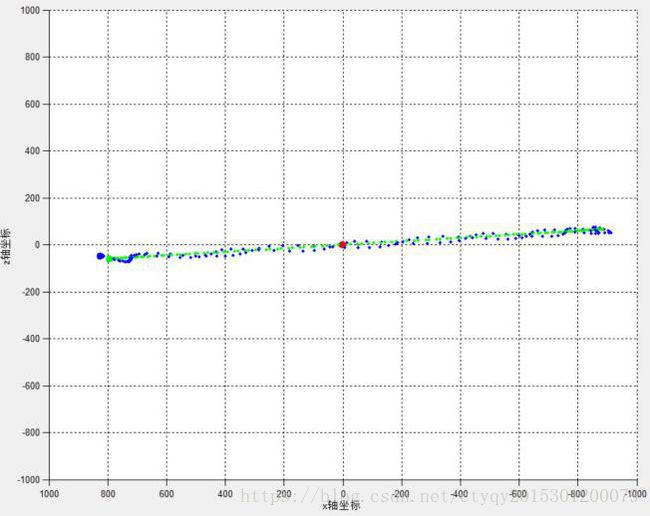图14 地月系统模型（2）

   上图中，红色星体是太阳，绿色星体是地球，蓝色星体是月球。首先是地球和月球构成双星系统，其次是太阳与地月系构成“准双星系统”。由于地-月、日-地月质量差异悬殊，故而在模型中太阳基本不发生移位，地球基本与太阳保持在同一平面内，而月球却不在此平面内，见图14的右图。

4.3.7 不规则三星系统

   不规则三星是三体模型中最一般的情况，条件为三质点质量相近、速度适中。在这种初始条件下，三星做无规则运动，无解析解、误差可累积，无序且无法长期预测。宇宙中的三星系统也较为常见，例如距离地球约4光年的半人马座α就是一个三合星系统的实例。实验产生的不规则三星系统运动效果如图15所示。

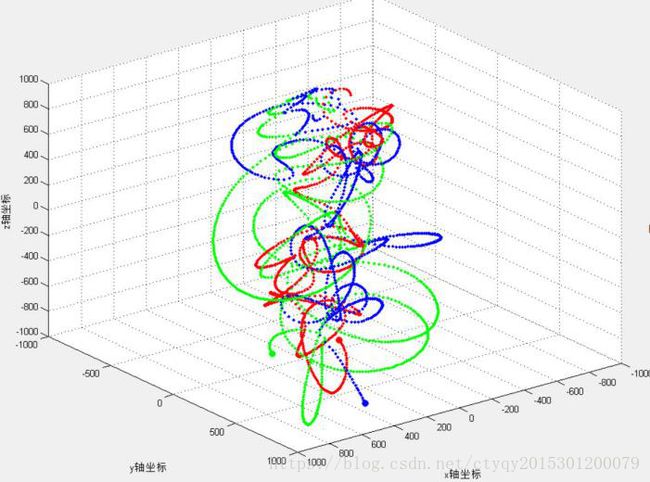图15 不规则三体系统（1）

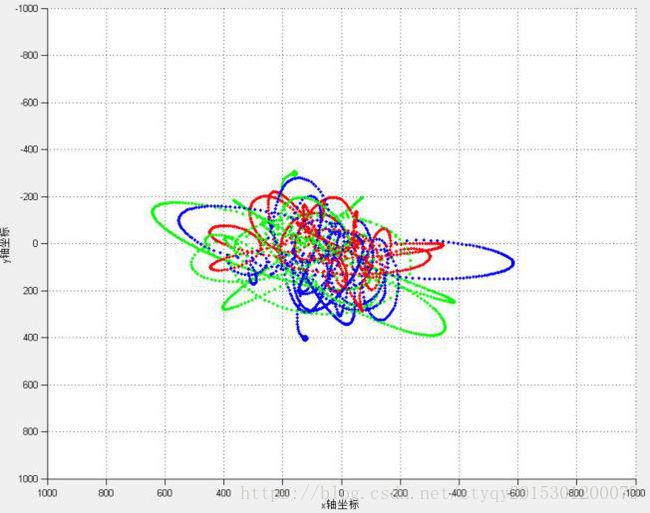图15 不规则三体系统（2）

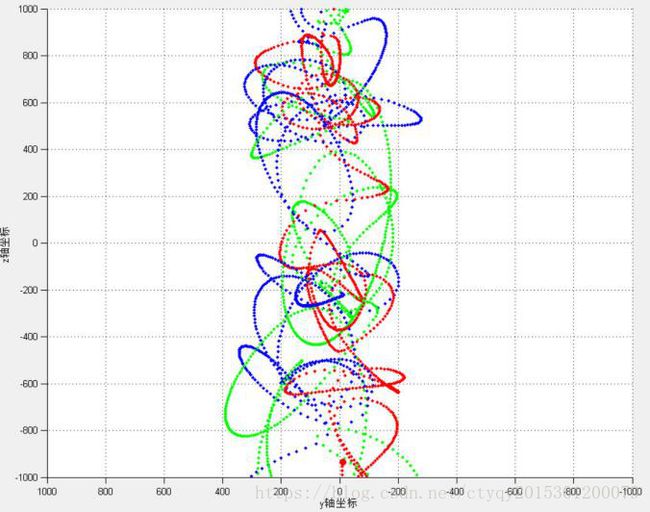图15 不规则三体系统（3）

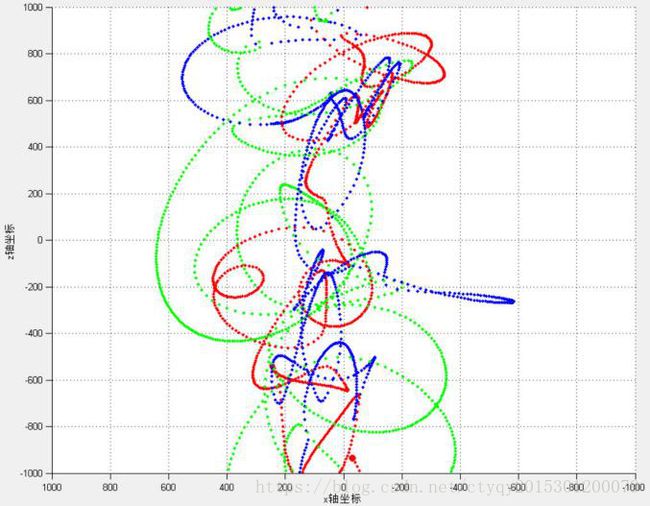图15 不规则三体系统（4）

   上图所示依次（从左到右、从上到下）为不规则三体系统运动轨迹的立体视图、XOY平面视图、YOZ平面视图以及XOZ平面视图，可见红绿蓝三星缠作一团，难以发现其规律。此类系统的归宿同样包括星体相撞破裂和星体逃逸两种。

4.3.8 星体碰撞

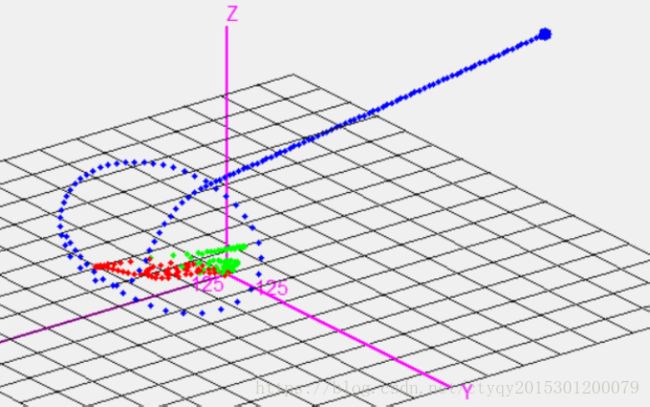
   图16所示是三体运动的一种可能。在运行一段时间后，红、绿两颗星体过于靠近，突破了星体安全运行了距离底线，触发了星体碰撞事件。本软件将星体间的碰撞简化为完全的、毁灭性的碰撞，参与碰撞的两颗星体失去星体结构，产生了大量四散的残骸，失去对第三颗星体的有效引力影响。故而图中的蓝色星体在红绿两星碰撞后近似匀速直线运动。

图16 星体碰撞湮灭

 

5 实验结论

   本实验成功建立了基于经典力学的三维自由空间三体运动模型，并利用MATLAB的GUI功能完成了可视化的实现。实验在验证已有三体问题的部分特解的同时对该运动模型的其他可能解作出探索，展现了若干种给定初始条件下的运动状态。

   在对已有数据的分析中，粗略验证了三体系统属于经典混沌系统这一基本事实，直观上验证了三体系统的无解析解和误差累积等基本特性。

 

6 后记

   这是我大三上学期某一门课程的一次作业，前前后后共花了大约1个月的课余时间。我主要是写了第一个版本的代码，还是主要靠一位大佬同学才改到了第二版本，第二版本相较于第一版本的改进主要是版面上、操作上美观了许多，这点在此必须说明清楚。

   我能想到用模拟三体运动模型作为那次作业的主题还得感谢刘慈欣，自从高三接触到他的著作《三体(三部曲)》之后就对这个主题深感兴趣，于是就一直有这个想法。当然我也借鉴了许多他山之石，比如叶飞影的博客和其他各种视频、代码资源等，当然我肯定没有大佬叶飞影做得好（emmm这点自知之明还是有的）。

   另外，MATLAB大概不是很擅长做这种图形显示的活，尤其是在没有显卡时很吃CPU，但是如果坚持数值模拟这条路不改变的话对运算量的要求必然是巨大的，个人笔记本只能非常粗糙地进行模拟。比如我的代码就是0.001s运算一次、每运算200次显示一次。如果再细致下去，非把CPU卡死不可。

   转载时务必注明来源及作者。尊重知识产权从我做起。

   代码已上传至网络，欢迎下载，密码是bezt。