算法与数据结构之美-线性排序

开篇思考

如何根据年龄给100万个用户进行排序？

桶排序(Bucket sort)

桶排序的概念就是将要排序的数据分到几个有序的桶里，每个桶里的数据在单独进行排序，桶内排序完之后，再把桶内的数据按照顺序依次取出，组成的序列就是有序的。

ton性能分析
桶排序的时间复杂度是O(n)
分析：
如果要排序的数据有n个，划分到m个桶内，那么每个桶内的数据就是n/m,对于每个桶内的数据采用快速排序，快排的时间复杂度是O(klogk),经过计算以后，桶排序的时间复杂度就是O(nlog(n/m)),当n和m的个数接近的时候，时间复杂度就趋向于O(n).

桶排序对于排序数据的要求严格，要排序的数据需要划分成m个桶，桶与桶之间是天然有序的，对每个桶排序完之后，桶与桶之间就不需要进行排序。

数据经过桶的划分之后要求是分布均匀的，在极端情况下，如果数据都被划分到一个桶内，那么就会退化成O(nlogn)的排序算法。

桶排序适用于外部排序，外部排序就是由于数据存储在外部磁盘中，数据量大，内存有限，无法全部加载到内存中。

思考题：
比如有10亿的订单数据，希望按照订单金额进行排序，但是内存有限只有几百M，不能一次性加载完所有数据，那么如何操作？

首先先扫描一遍文件，看看订单金额所在的数据范围；假设经过扫描之后，订单金额最小的是1元，最大是10万元，将所有订单根据金额划分到100个桶内，第一个桶内存储1-1000元的订单，第二个桶内存存储1001-2000元的订单，依次类推。每个桶对应一个文件，并且按照金额范围的大小顺序编号命名(00,01,01…99);

在理想的情况下，如果订单金额在1到10万之间均匀分布，那么订单就会均匀的分配划分到100个文件中，每个小文件存储大约100m左右的数据。当然订单金额在1到10万元不一定是均匀分布的，所以10GB的订单金额是无法均匀划分到100个文件中的，有可能某个区间内的数据特别多，划分完之后的文件还是很大。例如：1-1000元的区间，可以将这个区间继续划分为10个区间，如果划分完之后，还是无法读入内存就继续划分区间。

计数排序(Counting sort)

计数排序是桶排序的一种特殊情况，当要排序的数据范围不是很大的时候，比如最大值是k,就把数据划分到k个桶中，每个桶内的数据是相同的，省去了排序的时间；

以高考为例，考生有30万人，满分750，最低分是0分，就可以创建751个桶，对应的分数就是0-751分，依据高考成绩将30万考生划分到这些桶内；

那么计数排序的是怎么计数的呢？

例子：8位考生的考试分数分别为 2、5、3、0、2、3、0、3，那么数组A[8]内存储的就是考生的分数，考生的分数在0-5之间，采用6个桶，下标对应的就是考生的分数，桶内存储的不是考生，而是对应分数的考生个数，数组为C[6],如下图所示：

我们对C[6]数组进行顺序求和，就会得到C[k]数组，C[k]内存储的就是小于等于分数k的考生个数：

让我们开始这个计数过程吧！
考生的个数为8，所以需要创建一个大小为8的数组R[8]，其分数分别为2、5、3、0、2、3、0、3，当读入第一个分数为2时，C[2]=4，那么取出一个分数2，假如R[8]数组中对应的第四个位置，也就是R[3] = 2,对应的C[2]中因为取出一个2,所以C[2]需要减1,C[2]=3;
如下图所示：

继续当读入第二个分数为5时，C[5]等于8，取出插入R数组中第八个位置，就是下标为7的位置是R[7] = 5,C[5]-1 = 7;

当读入第三个元素为3时，C[3]=7，取出插入R数组中的第七个位置，就是下标为6的位置R[6] = 3,C[3]-1 =6;

当读入第四个元素为4为0时，C[0]=2,取出插入R数组中的第二个位置就是R[1] =0,C[0]-1=1;

当读入第五个元素为2时，C[2]=3，取出插入R数组中的第三个位置，就是R[2]=2,从C[2]-1=2;

当读入第六个元素为3时，C[3]=6,插入R数组中的第六个位置，R[5]=3,C[3]-1=5;

当读入第七个元素为0时，C[0]=1,插入R数组中的第一个位置，R[0]=0,C[0]-1=0;

当插入第八个元素为3时，C[3]=5,插入R数组的第五个位置，R[5]=3,C[3]-1 = 4;

最终得到的R数组就是排序后的数组，我觉得在看完之后，应该是能够理解整个计数排序的过程了，代码如下：

public class CountingSort {
    public static void main(String[] args){
        int[] a = {2,5,3,0,2,3,0,3};
        CountingSort(a,a.length);
        for(int i=0;i<a.length;i++){
            System.out.println(a[i]);
        }
    }
    public static void CountingSort(int [] a,int n){
        if(n<=1) return;
        //查找数组中的数据范围
        int max = a[0];
        for(int i=0;i<n;i++)
        {
            if(a[i]>max)
            {
                max = a[i];
            }
        }
        //申请一个数组c，下标为[0,max];
        int[] c = new int[max+1];
        for(int i=0;i<=max;i++)
            c[i] = 0;
        //计算每个元素的个数，并且放入到数组中
        for(int i=0;i<n;i++)
        {
            c[a[i]]++;
        }
        //在对每个下标对应的元素之和进行累加
        for(int i=1;i<=max;i++)
        {
            c[i]=c[i]+c[i-1];
        }
        //创建临时数组，存储排序之后的结果
        int[] temp = new int[n];
        for(int i=0;i<n;i++)
        {
            int k = c[a[i]]-1;
            temp[k] = a[i];
            c[a[i]]--;
        }
        //最后再将临时数组中的数据拷贝为a[i]中
        for(int i=0;i<n;i++){
            a[i] = temp[i];
        }
    }
}

基数排序(Radix sort)

上面说到了桶排序和计数排序，假如对手机号进行排序呢，可能数据量不大，但是范围太大，显然这两种排序算法是不合适的，那么就可以采用基数排序来实现；

借助稳定排序算法，可以先按照最后一位来排序手机号码，然后再按照倒数第二位进行排序，依次类推，经过11次排序之后，手机号码就都有序了，下面是一个基数排序过程的分解图：

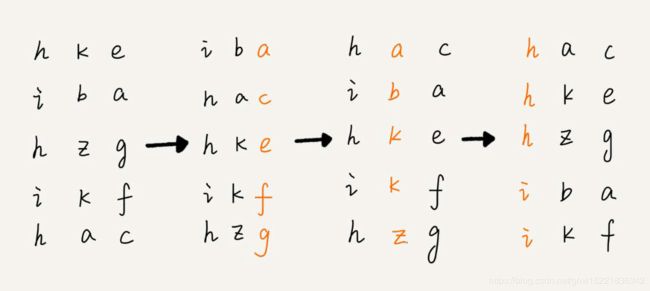
解答开篇

那么开篇思考如何根据年龄给100万用户排序呢？设定年龄为1-100岁，遍历100万用户，放到100个桶子里，再依次顺序遍历100个桶子，就得到了按照年龄排序的100万用户数据；