概率图之马尔可夫随机场(Markov Random Field,MRF)
现实生活中,许多任务涉及多个因素(变量),并且因素之间存在依赖关系。概率图模型(Probabilistic Graphical Model,PGM)为表示、学习这种依赖关系提供了一个强大的框架,概率图模型在形式上由图结构组成,一个节点(node)表示一个或一组随机变量,节点之间的边(edge)表示变量之间的关系。根据图是有向还是无向,概率图模型可以分为两类:第一类使用有向无环图表示变量之间的因果关系,称为有向图模型或贝叶斯网络(Bayesian network);另一类使用无向图表示变量之间的相关关系,称为无向图模型或马尔可夫网(Markov network),马尔可夫随机场(Markov Random Field)。概率图模型具有以下几个有用的性质:
- 它提供了一种简单的方式将概率模型的结构可视化,可以用于设计新的模型。
- 通过观察图形,我们可以更加深刻地认识模型的性质,包括条件独立性质。
- 高级模型的推断和学习过程中的复杂计算可以根据图计算表达,图隐式的承载了背后的数学表达式。
目前,概率图模型是人工智能领域最流行的研究方向之一,这篇博客主要介绍马尔可夫随机场。
模型定义
势函数
下图是一个简单的马尔可夫随机场:
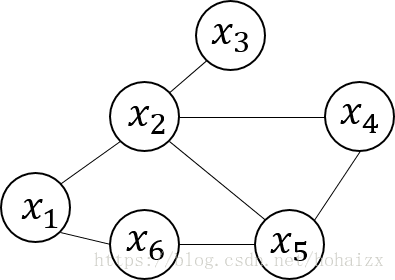
图中的边表示节点之间具有相互关系,这种关系是双向的、对称的。如: x 2 x_2 x2和 x 3 x_3 x3之间有边相连,则 x 2 x_2 x2和 x 3 x_3 x3具有相关关系,这种相关关系采用势函数进行度量。例如,可以定义如下势函数:
ψ ( x 2 , x 3 ) = { 1.5 if x 2 = x 3 ; 0.1 if o t h e r w i s e . \psi(x_2,x_3)=\begin{cases} 1.5 &\text{if } x_2=x_3;\\ 0.1 &\text{if } otherwise. \end{cases} ψ(x2,x3)={1.50.1if x2=x3;if otherwise.
则说明该模型偏好变量 x 2 x_2 x2与 x 3 x_3 x3拥有相同的取值,换言之,在该模型中, x 2 x_2 x2与 x 3 x_3 x3的取值正相关。势函数刻画了局部变量之间的相关关系,它应该是非负的函数。为了满足非负性,指数函数常被用于定义势函数:
ψ ( x ) = e − H ( x ) \psi(x)=e^{-H(x)} ψ(x)=e−H(x)
H ( x ) H(x) H(x)是一个定义在变量 x x x上的实值函数,常见形式为:
H ( x ) = ∑ u , v ∈ x , u ≠ v α u v x u x v + ∑ v ∈ x β v x v H(x)=\sum_{u,v\in x,u\neq v}{\alpha_{uv}x_ux_v+\sum_{v\in x}\beta_vx_v} H(x)=u,v∈x,u̸=v∑αuvxuxv+v∈x∑βvxv
其中 α u v \alpha_{uv} αuv和 β v \beta_v βv是需要学习的参数,称为参数估计。
MRF的马尔可夫性
马尔可夫随机场是生成式模型,生成式模型最关心的是变量的联合概率分布。假设我们有n个取值为二值随机变量( x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x1,x2,⋯,xn),其取值分布将包含 2 n 2^n 2n种可能,因此确定联合概率分布 p ( x 1 , x 2 , ⋯ , x n ) p(x_1,x_2,\cdots,x_n) p(x1,x2,⋯,xn)需要 2 n − 1 2^n-1 2n−1个参数,这个复杂度通常是我们不能接受的;而另一种极端情况是,当所有变量都相互独立时, p ( x 1 , x 2 , ⋯ , x n ) = p ( x 1 ) p ( x 2 ) ⋯ p ( x n ) p(x_1,x_2,\cdots,x_n)=p(x_1)p(x_2)\cdots p(x_n) p(x1,x2,⋯,xn)=p(x1)p(x2)⋯p(xn)只需要 n n n个参数。因此,我们可能会思考,能不能将联合概率分布分解为一组子集概率分布的乘积呢?那么应该怎么划分子图呢?应该遵循怎样的原则?首先定义马尔可夫随机场中随机变量之间的全局马尔可夫性、局部马尔可夫性和成对马尔可夫性。
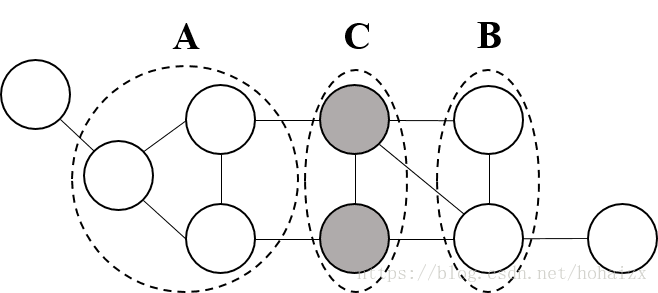
- 全局马尔可夫性(global Markov property):设节点集合A,B是在无向图G中被节点集C分开的任意节点集合,如下图所示。全局马尔可夫性是指在给定 x C x_C xC的条件下, x A x_A xA和 x B x_B xB条件独立,记为 x A ⊥ x B ∣ x C x_A\perp x_B|x_C xA⊥xB∣xC。
p ( x A , x B ∣ x C ) = p ( x A ∣ x C ) p ( x B ∣ x C ) p(x_A,x_B|x_C)=p(x_A|x_C)p(x_B|x_C) p(xA,xB∣xC)=p(xA∣xC)p(xB∣xC)
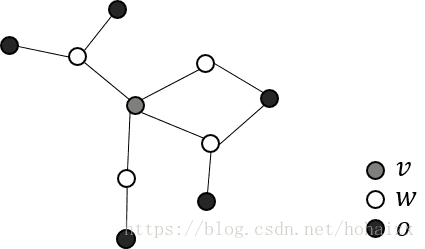
- 局部马尔可夫性(local Markov property):给定变量 v v v的所有邻接变量 w w w,则该变量 v v v条件独立于其他变量 o o o。即在给定某个变量的邻接变量的取值条件下,该变量的取值将于其他变量无关。
p ( x v , x v ∣ x w ) = p ( x v ∣ x w ) p ( x o ∣ x w ) p(x_v,x_v|x_w)=p(x_v|x_w)p(x_o|x_w) p(xv,xv∣xw)=p(xv∣xw)p(xo∣xw)
- 成对马尔可夫性(pairwise Markov property):给定所有其他变量,两个非邻接变量条件独立。这是因为两个节点没有直接路径,并且所有其他路径上都有确定的观测节点,因此这些路径也将被阻隔。
p ( x i , x j ∣ x ∖ { i , j } ) = p ( x i ∣ x ∖ { i , j } ) p ( x j ∣ x ∖ { i , j } ) p(x_i,x_j|x_{\setminus\{i,j\}})=p(x_i|x_{\setminus\{i,j\}})p(x_j|x_{\setminus\{i,j\}}) p(xi,xj∣x∖{i,j})=p(xi∣x∖{i,j})p(xj∣x∖{i,j})
其中 x ∖ { i , j } x_{\setminus\{i,j\}} x∖{i,j}表示所有变量 x x x去除 x i x_i xi和 x j x_j xj的集合。于是,联合概率分布的分解一定要让 x i x_i xi和 x j x_j xj不出现在同一个划分中,从而让属于这个图的所有可能概率分布都满足条件独立性质。(QA:这句话我也不太懂,欢迎大神指点)。让非邻接变量不出现在同一个划分中,即每一个划分中节点都是全连接的。这将我们引向了图的一个概念,团(clique)。它被定义为图中节点的一个子集,并且这个子集中任意两节点间都有边相连。若在一个团中加入其他任何节点都不再形成团,则称该团为极大团。下图给出了团和极大团的一个示意:

图中,绿色圆圈是一个团,蓝色圆圈是一个极大团。显然,最简单的团就是两个节点以及一条边,而我们最开始就针对两节点之间的相关关系(每条边)定义了势函数。因此,马尔可夫随机场中,多个变量的联合概率分布能基于团分解为多个势函数的乘积,每一个团对应一个势函数。
p ( x ) = 1 Z ∏ C ψ C ( x C ) p(x)=\frac{1}{Z}\prod_{C}\psi_C(x_C) p(x)=Z1C∏ψC(xC)
其中,如果C是一个团, ψ C \psi_C ψC为团C对应的势函数。 Z = ∑ x ∏ C ψ C ( x C ) Z=\sum_x\prod_{C}\psi_C(x_C) Z=∑x∏CψC(xC)是归一化因子,以确保 p ( x ) p(x) p(x)是正确定义的概率。对图中每一条边都定义一个势函数 ψ \psi ψ,将导致模型的势函数过多,带来计算负担。例如,最上面的图中 x 2 x_2 x2、 x 4 x_4 x4、 x 5 x_5 x5分别定义需要定义三个势函数,但是 x 2 x_2 x2、 x 4 x_4 x4、 x 5 x_5 x5两两相关, x 2 x_2 x2、 x 4 x_4 x4与 x 5 x_5 x5的取值将相互影响,因此可以整体定义一个势函数 ψ ( x 2 , x 4 , x 5 ) \psi(x_2,x_4,x_5) ψ(x2,x4,x5)表示三者取值的偏好。所以可以将联合概率分布分解为其极大团上的势函数的乘积:
p ( x ) = 1 Z ∗ ∏ Q ∈ C ∗ ψ Q ( x Q ) p(x)=\frac{1}{Z^*}\prod_{Q\in C^*}\psi_Q(x_Q) p(x)=Z∗1Q∈C∗∏ψQ(xQ)
其中 C ∗ C^* C∗是极大团构成的集合, Z ∗ = ∑ x ∏ Q ∈ C ∗ ψ Q ( x Q ) Z^*=\sum_x\prod_{Q\in C^*}\psi_Q(x_Q) Z∗=∑x∏Q∈C∗ψQ(xQ)。例如,最上面的图中 x = { x 1 , x 2 , ⋯ , x 6 } x=\{x_1,x_2,\cdots,x_6\} x={x1,x2,⋯,x6},联合概率分布 p ( x ) p(x) p(x)定义为
p ( x ) = 1 Z ψ 12 ( x 1 , x 2 ) ψ 16 ( x 1 , x 6 ) ψ 23 ( x 2 , x 3 ) ψ 56 ( x 5 , x 6 ) ψ 245 ( x 2 , x 4 , x 5 ) p(x)=\frac{1}{Z}\psi_{12}(x_1,x_2)\psi_{16}(x_1,x_6)\psi_{23}(x_2,x_3)\psi_{56}(x_5,x_6)\psi_{245}(x_2,x_4,x_5) p(x)=Z1ψ12(x1,x2)ψ16(x1,x6)ψ23(x2,x3)ψ56(x5,x6)ψ245(x2,x4,x5)
总结
马尔可夫随机场作为概率图模型的典型一类,用于对具有相关关系(无向)的变量分布进行建模,具有广泛的用用途,如图像去噪等。本篇博客主要介绍了马尔可夫随机场的定义,马尔可夫随机场中的条件独立,以及其联合概率分解方式,参数估计、推理等问题将单独介绍。
参考文献
读懂概率图模型:你需要从基本概念和参数估计开始
PGM:概率图模型Graphical Model
周志华-机器学习
李航-统计学习方法