数据结构——线段树(区间树)

一、为什么要使用线段树？

线段树又称为区间树，Segment Tree，对于有一类的问题，我们关心的是线段(或者区间)，有一个非常经典的例子：区间染色

问题1：有一面墙，长度为n，每次选择一段墙进行染色，n次操作后，我们可以在[i,j]区间内看见多少种颜色？

实际上这道题可以拆分为两个步骤：

①染色操作(更新区间)

②查询操作(查询区间)

如果都使用数组实现的话，染色和查询操作时间复杂度都为O(n)。

 

问题2：区间查询——查询一个区间[i,j]的最大值，最小值，或者区间数字和

问题的实质：基于区间的统计查询

如：2017年注册用户中消费最高的用户？消费最少的用户？学习时间最长的用户？

某个太空区间中天体总量？

 

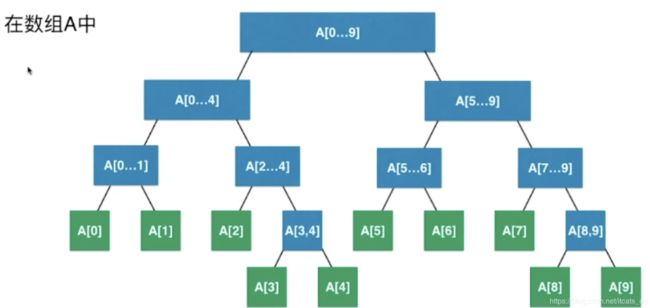
二、线段树是什么样子的？

在二叉树中，每一个节点存储的是一个线段或一个区间，如上图，每一个节点都对应一个线段的和值。

那么线段树是否一定为满二叉树/完全二叉树呢？——不一定，  且叶子节点不一定全都在树的最后一层！！！但线段树是一颗平衡二叉树(即最大深度与最小深度差值最大为1)，如图：

 

 

三、构建线段树

具体代码：

public interface Merger {
    E merge(E a , E b);
}

public class SegmentTree {
    private E[] data;
    private E[] tree;
    private Merger merger;

    public SegmentTree(E[] arr,Merger merger){
        this.merger = merger;
        data = (E[]) new Object[arr.length];
        for(int i = 0 ; i < arr.length ;i++){
            data[i] = arr[i];
        }
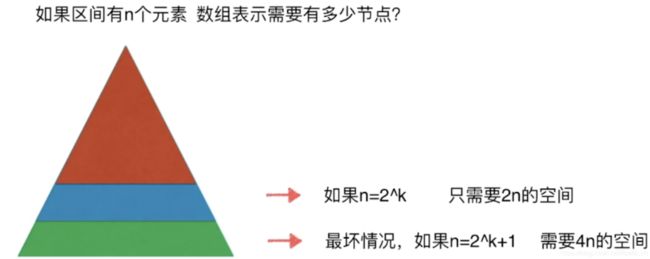
        tree = (E[]) new Object[4 * arr.length];
        //在treeIndex的位置创建表示区间从[l...r]的线段树
        buildSegmentTree(0,0,data.length - 1);
    }

    /**
     *
     * @param treeIndex 创建线段树所对应的根节点的索引
     * @param l 区间的左端点
     * @param r 区间的右端点
     */
    private void buildSegmentTree(int treeIndex,int l,int r) {
        if(l == r){
            tree[treeIndex] = data[l];
            return ;
        }

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        int mid = l + (r - l ) / 2 ;
        buildSegmentTree(leftTreeIndex , l , mid);
        buildSegmentTree(rightTreeIndex , mid + 1 , r);

        //综合两个子节点的信息得到父节点的信息,如求和操作
        tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
    }

    public int getSize(){
        return data.length;
    }

    public E get(int index){
        if(index < 0 ||index >= data.length){
            throw new IllegalArgumentException("参数错误");
        }
        return data[index];
    }

    private int leftChild(int index){
        return 2 * index + 1;
    }

    private int rightChild(int index){
        return 2 * index + 2;
    }
}

 

四、线段树中区间查询

    /**
     * @param queryL 查询左边界
     * @param queryR 查询右边界
     * @return
     */
    public E query(int queryL,int queryR){
        //确定边界
        if(queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length || queryL > queryR)
            throw new IllegalArgumentException("边界值异常");
        return query(0,0,data.length - 1 ,queryL ,queryR);
    }

//在以根节点为treeIndex的线段树中[l...r]的范围里,搜索区间[queryL...queryR]的值
    private E query(int treeIndex , int l , int r , int queryL ,int queryR) {
        if(l == queryL && r == queryR)
            return tree[treeIndex];
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        int mid = l + (r - l ) / 2 ;
        //忽略左部分
        if(queryL >= mid + 1)
            return query(rightTreeIndex,mid + 1 , r,queryL,queryR);
        //忽略右部分
        if(queryR <= mid)
            return query(leftTreeIndex,l,mid,queryL,queryR);
        //并没有完全落在左节点或者右节点中,一部分落在左边,一部分落在右边
        E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
        return merger.merge(leftResult,rightResult);
    }

 

五、参考题目

参考Leetcode上303题《区域和检索 - 不可变》

给定一个整数数组  nums，求出数组从索引 i 到 j  (i ≤ j) 范围内元素的总和，包含 i,  j 两点。

相关链接：https://leetcode-cn.com/problems/range-sum-query-immutable/description/

可以使用线段树进行解答：

public class NumArray {

    private SegmentTree segmentTree;
    public NumArray(int[] nums) {
        if(nums.length > 0){
            Integer[] data = new Integer[nums.length];
            for(int i = 0 ; i < nums.length ; i++){
                data[i] = nums[i];
            }
            segmentTree = new SegmentTree(data,(a,b) -> a + b);
        }
    }
    
    public int sumRange(int i, int j) {
        if(segmentTree == null)
            throw new IllegalArgumentException("segmentTree is null,请考虑数组是否为空");
        return segmentTree.query(i,j);
    }
}

由于数据是不可变的，我们不使用线段树，也可以得到更好的解答。来看看不使用线段树的解题思路：

public class NumArray {

    private int [] sum; //sum中存储着前i个元素的和,sum[0] = 0
                        //sum[i]存储着nums[0...i-1]的和
    public NumArray(int[] nums) {
        sum = new int[nums.length + 1];
        sum[0] = 0 ;
        for(int i = 1 ; i < sum.length ; i ++)
            sum[i] = sum[i - 1] + nums[i - 1];
    }
    
    public int sumRange(int i, int j) {
        return sum[j + 1] - sum[i];
     }
}

可见对于数据不可变的情况下，线段树的优势并没体现出来，线段树主要是应用在数据是动态变化的场景。

 

参考Leetcode上307题：https://leetcode-cn.com/problems/range-sum-query-mutable/description/

 区域和检索 - 数组可修改

 

 

 

 

 

 

 

 

此时我们可以来看看不使用线段树的解题思路：

public class NumArray {
    private int [] sum; //sum中存储着前i个元素的和,sum[0] = 0
                        //sum[i]存储着nums[0...i-1]的和
    private int[] data;

    public NumArray(int[] nums) {
        data = new int[nums.length];
        for(int i = 0 ; i < nums.length ; i++)
            data[i] = nums[i];
        sum = new int[nums.length + 1];
        sum[0] = 0 ;
        for(int i = 1 ; i < sum.length ; i ++)
            sum[i] = sum[i - 1] + nums[i - 1];
    }

    public void update(int index , int val){
        data[index] = val;
        for(int i = index + 1; i < sum.length ; i++)
            sum[i] = sum [i - 1] + data[i - 1];
    }

    public int sumRange(int i, int j) {
        return sum[j + 1] - sum[i];
    }
}

这种操作时间复杂度略高，虽然sumRange依然是O(1)复杂度，但update是一个O(n)复杂度，最坏情况需要遍历nums.length次，如果测试用例中频繁使用update，则每次都是O(n)复杂度，进行m次update操作的话则时间复杂度是O(m*n)，性能较低。

 

下面我们使用线段树中更新操作O(logn)

public void set(int index , E e){
        if(index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index越界");
        data[index] = e;
        set(0,0,data.length-1,index,e);
    }

    private void set(int treeIndex, int l, int r, int index, E e) {
        if(l == r){
            tree[treeIndex] = e;
            return;
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if(index >= mid + 1){
            set(rightTreeIndex,mid + 1,r,index,e);
        }else
            set(leftTreeIndex,l,mid,index,e);
        tree[treeIndex] = merger.merge(tree[leftTreeIndex],tree[rightTreeIndex]);
    }