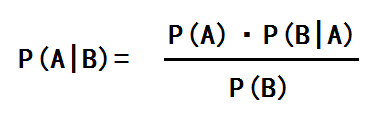算法高级(43)-过滤垃圾邮件、短信?-朴素贝叶斯算法
一、算法介绍
朴素贝叶斯算法,简称NB算法,是贝叶斯决策理论的一部分,是基于贝叶斯定理与特征条件独立假设的分类方法。
两个重要概念:
- 先验概率是指根据以往经验和分析得到的概率,它往往作为“由因求果”问题中的“因”出现。是我们在未知条件下对事件发生可能性猜测的数学表示;
- 后验概率是指在得到“结果”的信息后重新修正的概率,是“执果寻因”问题中的“因” 。事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小。
贝叶斯定理
贝叶斯理论是以18世纪的一位神学家托马斯·贝叶斯(Thomas Bayes)命名。通常,事件A在事件B(发生)的条件下的概率,与事件B在事件A(发生)的条件下的概率是不一样的;然而,这两者是有确定的关系的,贝叶斯定理就是这种关系的陈述。贝叶斯公式:
- P(A|B) 是在 B 发生的情况下 A 发生的概率,即后验概率;
- P(A) 是 A 发生的概率,即先验概率;
- P(B|A) 是在 A 发生的情况下 B 发生的概率;
- P(B) 是 B 发生的概率。
也可以认为A是类别,B是特征,于是可以表示为:
二、贝叶斯定理举例
为了更形象地对贝叶斯定理进行说明,给大家举两个例子。
1.基于贝叶斯的降水概率问题
假设今天早上小明要出门,但是发现外面天空是多云状态,那么今天会不会下雨呢,或者说多云的情况下今天的降水概率是多少呢?
事件A:今天下雨
事件B:早上有云
事件 A|B:早上有云,今天下雨
事件 B|A:今天下雨,早上有云
P(A):今天下雨的概率
P(B):早上有云的概率
P(A|B):早上有云的话,今天下雨的概率
P(B|A):今天下雨的话,早上有云的概率
小明现在要计算的是今天早上有云,今天的降水概率是多少,即P(雨|云) = P(雨)·P(云|雨) / P(云)
假设:80% 的雨天早上是有云的,30% 的早上都是有云的,这几个月很干旱,平均每个月(30 天)下雨的天数是 6 天。
那么P(雨|云) = 20% * 80% / 30% = 5.333%。
即今天的降水概率为5.333%,几乎可以认为今天不下雨。
2.假阳性和假阴性的检测。
有一天小明收到一束花,过了一会突然感觉全身发痒,于是小天去做了个简单的过敏检测:
真的过敏的人,检测会给“有”的概率是 90%
没有过敏的人,检测给“有”的概率是5%,这被称为假阳性
现在已知的条件是小明所在的市区中有 1% 的人有这种过敏,而小明去检测得到的结果是“有”,那么小天真正过敏的概率是多少呢?
P(过敏|有) = P(过敏) · P(有|过敏) / P(有)
观察公式发现,P(有)不知道,即我们不知道检测得到结果是“有”的一般可能性是多少。考虑一下如何计算P(有)。
根据已知条件可以得到:
1% 的人是真的过敏的,得到“有”的概率是 90%
99% 的人是没有过敏的,得到“有”的概率是 5%
所以P(有) = P(过敏)·P(有|过敏) + P(不过敏)·P(有|不过敏) = 1% × 90% + 99% × 5% = 5.85%
最终,小明计算得到了他真正过敏的概率:
P(过敏|有) = 1% × 80% / 5.85% = 13.68%。
三、垃圾邮件、短信的常规过滤方式
1. 基于黑名单过滤
可以维护一个骚扰电话号码、垃圾短信发送号码、垃圾邮件发送地址的黑名单。
- 黑名单的搜集,有很多途径,比如,公开的网站下载,用户自主标记。标记个数超过一定阈值的号码,我们就可以定义为骚扰电话,并将它加入到我们的黑名单中。
- 如果黑名单中的电话号码不多的话,我们可以使用散列表、二叉树等动态数据结构来存储,对内存的消耗并不会很大。如果我们把每个号码看作一个字符串,并且假设平均长度是16个字节,那存储50万个电话号码,大约需要10MB的内存空间。对于手机这样的内存有限的设备来说,这点内存的消耗也是可以接受的。
- 黑名单中的电话号码很多呢?比如有500万个。这个时候,如果再用散列表存储,就需要大约100MB的存储空间。为了实现一个拦截功能,耗费如此多的手机内存,显然有点不合理。
- 布隆过滤器最大的特点就是比较省存储空间,所以,用它来解决这个问题再合适不过。如果我们要存储500万个手机号码,我们把位图大小设置为10倍数据大小,也就是5000万,那也只需要使用5000万个二进制位(5000万bits),换算成字节,也就是不到7MB的存储空间。比起散列表的解决方案,内存的消耗减少了很多。
- 时间换空间,把黑名单存储在服务器端上,把过滤和拦截的核心工作,交给服务器端来做。手机端只负责将要检查的号码发送给服务器端,服务器端通过查黑名单,判断这个号码是否应该被拦截,并将结果返回给手机端。这个解决思路完全不占用手机内存。不过网络通信是比较慢的,所以,网络延迟就会导致处理速度降低。而且必须联网。
- 布隆过滤器会有判错的概率!如果它把一个重要的电话或短信,当成垃圾拦截了,对于用户来说,这是无法接受的。这是一个很大的问题。
2. 基于规则过滤
如果某个垃圾短信发送者的号码并不在黑名单中,那这种方法就没办法拦截了。所以,基于黑名单的过滤,还不够完善,再继续看基于规则的过滤。
通过短信的内容,来判断是垃圾短信。预先设定一些规则,如果短信符合这些规则,就判定它是垃圾短信。规则可以有很多,比如:
- 短信中包含特殊单词(或词语),比如一些非法、淫秽、反动词语等;
- 发送号码是群发号码,非正常的手机号码,比如+10123456****;
- 短信中包含回拨的联系方式,比如手机号码、微信、QQ、网页链接等,因为群发短信的号码一般都是无法回拨的;
- 短信格式花哨、内容很长,比如包含各种表情、图片、网页链接等;
- 符合已知垃圾短信的模板。与模板匹配,就可以判定为垃圾短信。
可以综合多条规则进行判断。比如,满足2条以上才会被判定为垃圾短信;
或者每条规则对应一个不同的得分,某条短信的总得分超过某个闽值,才会被判定为垃圾短信。
以上两种过滤,比较符合我们的想法,也有广泛应用,如网站维护的IP白名单、黑名单,以及定义的防火墙规则,其实都是上面所讲的。
四、基于概率统计的朴素贝叶斯分类过滤
朴素贝叶斯定理通常应用于人工智能领域,最常见的是朴素贝叶斯分类算法,也就是接下来要实现的基于概率的过滤器,本质上是通过计算概率来判断。
对于一条短信,我们通常可以通过这个短信的内容进行判断是否为垃圾短信。对于计算机来说无法直接通过内容来判断,但是我们可以将短信内容中的一些特征项提取出来,供计算机判断。
通过分词算法可以将短信内容分割成由n个单词的组合,那么现在的问题就变成了包含这些单词的短信是垃圾短信的概率是多少。
P(是垃圾短信 | 单词1、单词2 ... 单词 n 同时出现) = ?%我们使用朴素贝叶斯定理,将这个概率转换成其他三个概率来求解:
推导过程:
- P
(是垃圾短信)的值很容易计算,样本中垃圾短信数与样本总数之比即可得到。 - P(单词1、单词2 ... 单词 n 同时出现|是垃圾短信)
根据独立事件发生的概率计算公式:P(A*B) = P(A)*P(B)拆分为:
P(单词1、单词2 ... 单词 n 同时出现|是垃圾短信)=P(单词1|是垃圾短信)*P(单词2|是垃圾短信)*...*P(单词 n |是垃圾短信)。
P(单词i 出现在短信中 | 是垃圾短信)表示垃圾短信中包含单词i 这个单词的概率。
- P(单词1、单词2 ... 单词 n 同时出现),不去计算。
推导到这里,我们发现唯一不好计算的就是分母,那我们再次发散思维,我们可以分别计算一条短信是垃圾短信和非垃圾短信的概率,然后计算他们的倍数,如果倍数相差悬殊,那么我们就可以认为是垃圾短信。例如:
假设是垃圾短信的概率是p1,不是垃圾短信的概率是p2,这样一来,可以通过计算p1与p2的倍数关系来最终确定是否为垃圾短信,例如若p1是p2的十倍,那么可以认为短信一定是垃圾短信了。公式如下:
我们只需要计算p1/p2就能得出是否是垃圾短信了。
大家其实也看得出来,分母可以被约分约掉的。
实际上,我们可以结合三种不同的过滤方式的结果,对同一个短信处理,如果三者都表明这个短信是垃圾短信,才把它当作垃圾短信拦截过滤,这样就会更精准。同时,需要大量的实验,不断调整策略,并且需要权衡最终的准确率以及是否能把所有垃圾短信都找到。
五、总结
"概率论只不过是把常识用数学公式表达了出来"---拉普拉斯。
之所以贝叶斯方法在机器学习中如此重要,就是因为人们希望机器人能像人那样思考,而很多问题是需要计算机在已知条件下做出最佳决策的决策,而贝叶斯公式就是对人脑在已知条件下做出直觉判断的一种数学表示。
朴素贝叶斯的主要优点有:
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对小规模的数据表现很好,能个处理多分类任务,适合增量式训练。
- 对缺失数据不太敏感,算法比较简单,常用于文本分类。
- 可应用于图像识别。
朴素贝叶斯的主要缺点有:
- 理论上朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此。因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果并不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
- 需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
- 由于是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
- 对输入数据的表达形式很敏感。
我的微信公众号:架构真经(id:gentoo666),分享Java干货,高并发编程,热门技术教程,微服务及分布式技术,架构设计,区块链技术,人工智能,大数据,Java面试题,以及前沿热门资讯等。每日更新哦!
参考阅读:
- https://blog.csdn.net/m0_37264516/article/details/87481785
- https://blog.csdn.net/qq_21201267/article/details/98695641
- https://www.cnblogs.com/love528/p/10125089.html