matlab 万能实用的线性曲线拟合方法
在科学计算和工程应用中,经常会遇到需要拟合一系列的离散数据,最近找了很多相关的文章方法,在这里进行总结一下其中最完整、几乎能解决所有离散参数线性拟合的方法
第一步:得到散点数据
根据你的实际问题得到一系列的散点
例如:
x=[3.2,3.6,3.8,4,4.2,4.8,5,5.4,6.2,6.4,6.6,6.9,7.1]';%加上一撇表示对矩阵的转置
y=[0.38,0.66,1,0.77,0.5,0.66,0.83,1,0.71,0.71,1,0.87,0.83]';第二步:确定函数模型
根据上述的实际散点确定应该使用什么样的曲线,或者说是想要模拟的曲线
t=[3.2,3.6,3.8,4,4.2,4.8,5,5.4,6.2,6.4,6.6,6.9,7.1]';
tt=[0.38,0.66,1,0.77,0.5,0.66,0.83,1,0.71,0.71,1,0.87,0.83]';
plot(t,tt,'.');%得到散点图 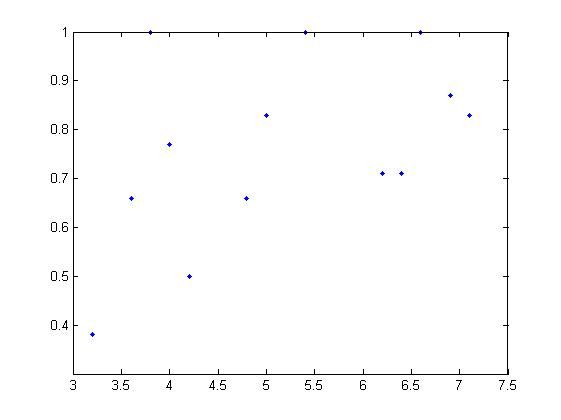
matlab中现成的函数:ployfit()
定义:polyfit函数是matlab中用于进行曲线拟合的一个函数。其数学基础是最小二乘法曲线拟合原理。曲线拟合:已知离散点上的数据集,即已知在点集上的函数值,构造一个解析函数(其图形为一曲线)使在原离散点上尽可能接近给定的值。
调用方法:polyfit(x,y,n)。用多项式求过已知点的表达式,其中x为源数据点对应的横坐标,可为行向量、矩阵,y为源数据点对应的纵坐标,可为行向量、矩阵,n为你要拟合的阶数,一阶直线拟合,二阶抛物线拟合,并非阶次越高越好,看拟合情况而定。
matlab polyfit 做出来的值从左到右表示从高次到低次的多项式系数。
例子:
x = (0: 0.1: 2.5)';
y = erf(x);
p = polyfit(x,y,6)
p =
0.0084 -0.0983 0.4217 -0.7435 0.1471 1.1064 0.0004 则y=0.0084x^6-0.0983x^5+0.4217x^4-0.7435x^3+0.1471x^2+1.1064x+0.0004
完整例子程序:
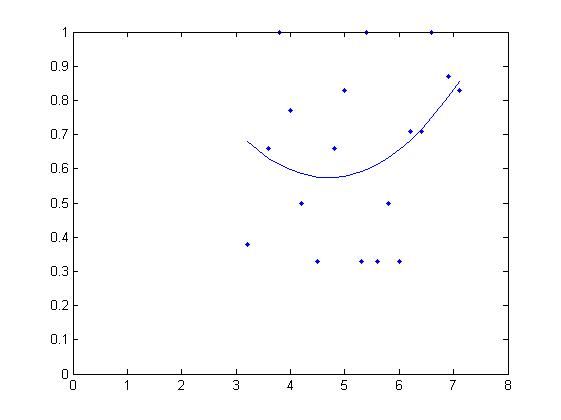
%二项式拟合
t=[3.2,3.6,3.8,4,4.2,4.5,4.8,5,5.3,5.4,5.6,5.8,6,6.2,6.4,6.6,6.9,7.1];
y=[0.38,0.66,1,0.77,0.5,0.33,0.66,0.83,0.33,1,0.33,0.5,0.33,0.71,0.71,1,0.87,0.83];
plot(t,y,'.');
hold on
p=polyfit(t,y,2)
y1=polyval(p,t);
axis([0,8,0,1]);
plot(t,y1)
%plot是画图函数
%polyval是求值函数
%polyfit是曲线拟合函数
%polyfit用于多项式曲线拟合
%p=polyfit(x,y,m)
%其中, x, y为已知数据点向量, 分别表示横,纵坐标, m为拟合多项式的次数, 结果返回m次拟合多项式系数, 从高次到低次存放在向量p中.
%y0=polyval(p,x0)
%可求得多项式在x0处的值y0结果:另外可以自行加上对应的横纵坐标内容,这里就不多说了。
总结一下matlab非线性拟合散点图的过程:得到散点数据=>确定线性函数模型=>求解函数模型的待定系数=>得到拟合函数的具体形式=>画出拟合图像