24点
- 作业题目
24点游戏是经典的纸牌益智游戏。
常见游戏规则:
从扑克中每次取出4张牌。使用加减乘除,第一个能得出24者为赢。(其中,J代表11,Q代表12,K代表13,A代表1),按照要求编程解决24点游戏。
基本要求: 随机生成4个代表扑克牌牌面的数字字母,程序自动列出所有可能算出24的表达式,用擅长的语言(C/C++/Java或其他均可)实现程序解决问题。
1.程序风格良好(使用自定义注释模板)
2.列出表达式无重复。
提高要求:用户初始生命值为一给定值(比如3),初始分数为0。随机生成4个代表扑克牌牌面的数字或字母,由用户输入包含这4个数字或字母的运算表达式(可包含括号),如果表达式计算结果为24则代表用户赢了此局。
1. 程序风格良好(使用自定义注释模板)
2.使用计时器要求用户在规定时间内输入表达式,如果规定时间内运算正确则加分,超时或运算错误则进入下一题并减少生命值(不扣分)。
3.所有成绩均可记录在TopList.txt文件中。
- 算法思路
计算模式:(m + n) + p ) + q
— — —
* * *
/ / /
其中“—”和“/”根据数字大小调整顺序(使得结果不存在负数或小于1的小数)
首先,依次进行前两位数(m、n),前三位数(m、n、p)和前四位数(m、n、p、q)的计算,依次得到3组数:第一组中有4个数、第二组中有16个数、第三组中有64个数。
其次,记录64组数中结果为24的数字角标。对数字角标进行“//”运算和求余运算,得到的商为前组对应数字角标,得到的余数为0,1,2,3,依次代表加、减、乘、除四则运算符。通过此种方式进行寻迹,然后组合。
最终,罗列出能够计算出24的表达式。
· 程序源代码
"""
@文件:24点
@说明:从扑克中每次取出4张牌。使用加减乘除,第一个能得出24者为赢。(其中,J代表11,Q代表12,K代表13,A代表1).
@时间:2019.4.15
"""
import random
import datetime
# 随机数产生
def random_number():
f_number = random.randint(1, 13)
s_number = random.randint(1, 13)
t_number = random.randint(1, 13)
o_number = random.randint(1, 13)
return f_number, s_number, t_number, o_number
# 前两位数计算
def Two_cacular(f_number, s_number):
x2 = 0
x1 = f_number + s_number
if f_number > s_number:
x2 = f_number - s_number
if f_number < s_number:
x2 = s_number - f_number
x3 = f_number * s_number
if f_number % s_number == 0:
x4 = f_number/s_number
elif s_number % f_number == 0:
x4 = s_number / f_number
else:
x4 = None
return x1, x2, x3, x4
# 前三位数计算
# x为前两位数计算结果
def Three_cacular(x, t_number):
y2 = 0
y1 = x + t_number
if x > t_number:
y2 = x - t_number
if x < t_number:
y2 = t_number - x
y3 = x * t_number
if x % t_number == 0:
y4 = x / t_number
elif t_number % x == 0:
y4 = t_number / x
else:
y4 = None
return y1, y2, y3, y4
# 四位数计算
# y为前三位数计算结果
def Four_cacular(y, o_number):
z2 = 0
z1 = y + o_number
if y > o_number:
z2 = y - o_number
if y < o_number:
z2 = o_number - y
z3 = y * o_number
if y % o_number == 0:
z4 = y / o_number
elif o_number % y == 0:
z4 = o_number / y
else:
z4 = None
return z1, z2, z3, z4
# 游戏过程
def Play_():
start_time = datetime.datetime.now() # 起始时间
cacular = input("一分钟内请计算:")
end_time = datetime.datetime.now() # 终止时间
cacular = eval(cacular) # 对输入字符串表达式转化为表达式并计算
time = end_time - start_time
return time, cacular
if __name__ == "__main__":
print("产生的随机数为:")
f_number, s_number, t_number, o_number = random_number()
print(f_number, s_number, t_number, o_number)
random_number = [str(f_number), str(s_number), str(t_number), str(o_number)]
x1, x2, x3, x4 = Two_cacular(f_number, s_number)
two_cal_result = [x1, x2, x3, x4] # 前两位随机数计算结果记录
three_cal_result = [] # 前三位随机数计算结果记录
four_cal_result = [] # 四位随机数计算结果记录
index_result = [] # 角标结果记录
life = 3 # 生命值
grade = 0 # 分数
while life != 0:
time, cacular = Play_()
if time.seconds >= 60:
print("超时!!!")
life = life - 1
continue
if cacular != 24:
print("计算错误!!!")
life = life - 1
continue
if cacular == 24:
print("计算正确!!!")
grade = grade + 1
openfile = open("TopList.txt", 'w') # 文件打开
openfile.write("最终成绩:%s" % str(grade)) # 文件写入
openfile.close() # 文件关闭
if life == 0:
print("Game Over!!!")
for k in range(0, 4):
if two_cal_result[k] == None:
three_cal_result.append(None)
three_cal_result.append(None)
three_cal_result.append(None)
three_cal_result.append(None)
elif two_cal_result[k] != None:
y1, y2, y3, y4 = Three_cacular(two_cal_result[k], t_number)
three_cal_result.append(y1)
three_cal_result.append(y2)
three_cal_result.append(y3)
three_cal_result.append(y4)
for u in range(0, len(three_cal_result)):
if three_cal_result[u] == None:
four_cal_result.append(None)
four_cal_result.append(None)
four_cal_result.append(None)
four_cal_result.append(None)
elif three_cal_result[u] != None:
z1, z2, z3, z4 = Four_cacular(three_cal_result[u], o_number)
four_cal_result.append(z1)
four_cal_result.append(z2)
four_cal_result.append(z3)
four_cal_result.append(z4)
for g in range(0, len(four_cal_result)):
if four_cal_result[g] == 24 or four_cal_result[g] == 24.0:
index_result.append(g)
# 余0为+,余1为-,余2为*,余3为/,商为前位角标,余数为四则运算符
for h in range(0, len(index_result)):
cacular_result = [] # 运算记录
string_cacular_result = "" # 运算结果字符串化
quotient3 = index_result[h] // 4
remainder3 = index_result[h] % 4
quotient2 = quotient3 // 4
remainder2 = quotient3 % 4
remainder1 = quotient2 % 4
cacular_result.append('(')
if remainder1 == 0:
cacular_result.append(f_number)
cacular_result.append('+')
cacular_result.append(s_number)
elif remainder1 == 1:
if f_number > s_number:
cacular_result.append(f_number)
cacular_result.append('-')
cacular_result.append(s_number)
if f_number < s_number:
cacular_result.append(s_number)
cacular_result.append('-')
cacular_result.append(f_number)
elif remainder1 == 2:
cacular_result.append(f_number)
cacular_result.append('*')
cacular_result.append(s_number)
elif remainder1 == 3:
if f_number > s_number:
cacular_result.append(f_number)
cacular_result.append('/')
cacular_result.append(s_number)
if f_number < s_number:
cacular_result.append(s_number)
cacular_result.append('/')
cacular_result.append(f_number)
cacular_result.append(')')
cacular_result.insert(0, '(')
if remainder2 == 0:
cacular_result.append('+')
cacular_result.append(t_number)
elif remainder2 == 1:
if two_cal_result[quotient2] > t_number:
cacular_result.append('-')
cacular_result.append(t_number)
if two_cal_result[quotient2] < t_number:
cacular_result.insert(1, t_number)
cacular_result.insert(2, '-')
elif remainder2 == 2:
cacular_result.append('*')
cacular_result.append(t_number)
elif remainder2 == 3:
if two_cal_result[quotient2] > t_number:
cacular_result.append('/')
cacular_result.append(t_number)
if two_cal_result[quotient2] < s_number:
cacular_result.insert(1, t_number)
cacular_result.insert(2, '/')
cacular_result.append(')')
if remainder3 == 0:
cacular_result.append('+')
cacular_result.append(o_number)
elif remainder3 == 1:
if three_cal_result[quotient3] > o_number:
cacular_result.append('-')
cacular_result.append(o_number)
if three_cal_result[quotient3] < o_number:
cacular_result.insert(0, o_number)
cacular_result.insert(1, '-')
elif remainder3 == 2:
cacular_result.append('*')
cacular_result.append(o_number)
elif remainder3 == 3:
if three_cal_result[quotient3] > o_number:
cacular_result.append('/')
cacular_result.append(o_number)
if three_cal_result[quotient3] < o_number:
cacular_result.insert(0, o_number)
cacular_result.insert(1, '/')
cacular_result.append('=')
cacular_result.append(24)
for j in range(0, len(cacular_result)):
string_cacular_result += str(cacular_result[j])
print("第%d种运算结果:" % (h+1))
print(string_cacular_result)
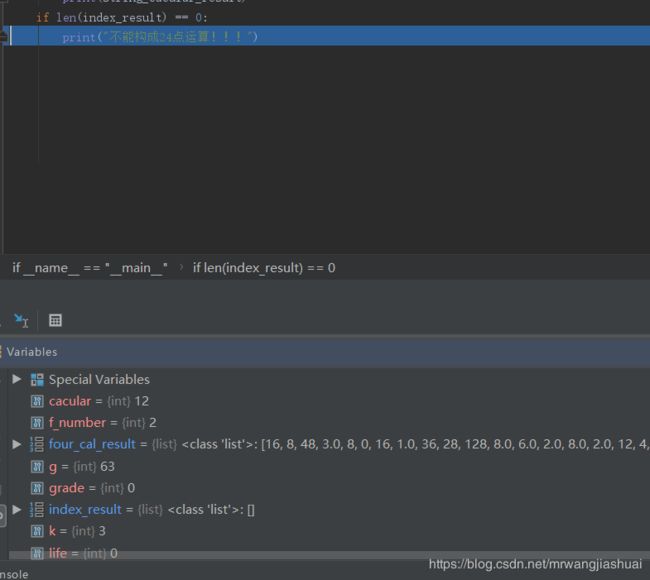
if len(index_result) == 0:
print("不能构成24点运算!!!")
三、调试、测试及运行结果
调试
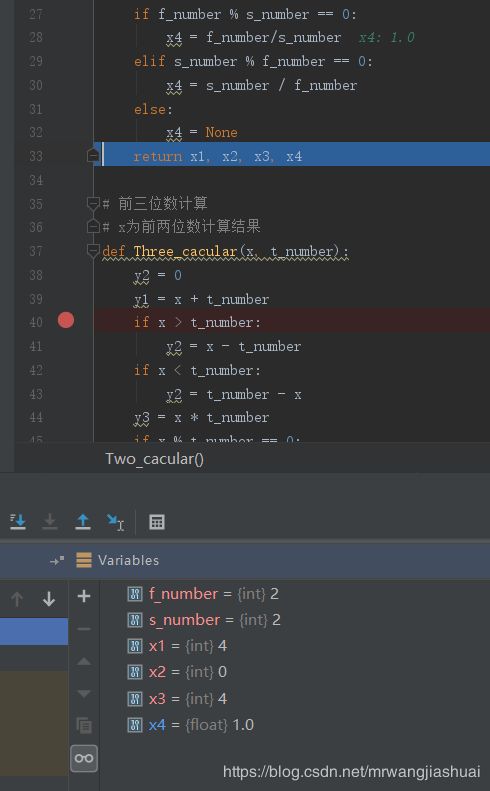
随机数生成,已生成两位为“2”、“2”
random函数
前两位数(7、9)进行计算,加减乘除得:4、0、4、1.0.
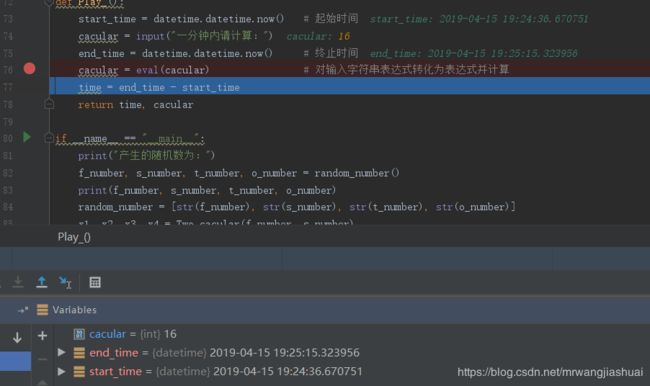
计时与字符串表达式计算,2+2+8+4,计算结果为16
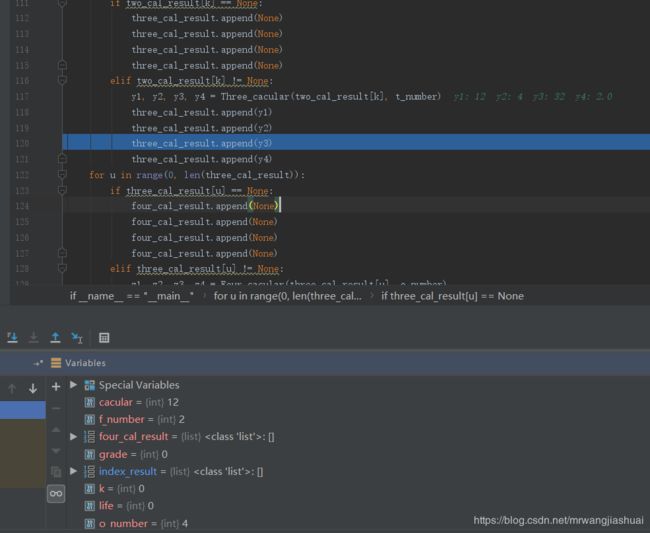
前三位数计算并添加过程
前四位数计算并添加过程
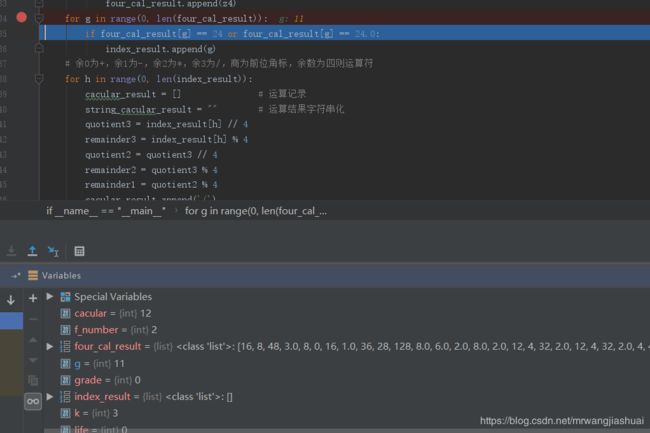
在64个结果中查找24——>统计角标
调查结果完毕,本组数(2,2,8,4)不能构成24点运算
测试及运行结果
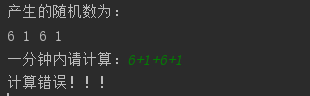
初始界面
计算结果非24点(错误计算)
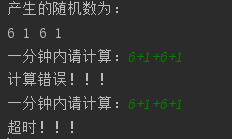
计算超时测试
三点生命值耗尽,游戏结束,公示答案:本组数不能构成24点运算
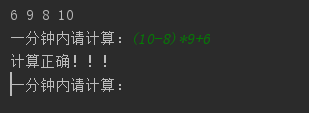
正确计算测试
四、总结
1、本程序提出了一种一组数罗列24点所有运算方法的方法。即:
计算模式:(m + n) + p ) + q
— — —
* * *
/ / /
基于上述计算模式。
其中“—”和“/”根据数字大小调整顺序(使得结果不存在负数或小于1的小数)
首先,依次进行前两位数(m、n),前三位数(m、n、p)和前四位数(m、n、p、q)的计算,依次得到3组数:第一组中有4个数、第二组中有16个数、第三组中有64个数。
其次,记录64组数中结果为24的数字角标。对数字角标进行“//”运算和求余运算,得到的商为前组对应数字角标,得到的余数为0,1,2,3,依次代表加、减、乘、除四则运算符。通过此种方式进行寻迹,然后组合。
最终,罗列出能够计算出求解24的表达式。
2、eval()函数
通过本程序学习到了新的函数eval()函数
eval(source[, globals[, locals]])
作用:
将字符串str当成有效的表达式来求值并返回计算结果。参数:source:一个Python表达式或函数compile()返回的代码对象;globals:可选。必须是dictionary;locals:可选。任意map对象。