漫画算法-小灰的算法之旅-算法的实际应用（六）

 

1. Bitmap的巧用

1.1 查询

1.2 去重

1.3 Bitmap的代码实现

2. LRU算法的应用

2.1 实例问题

2.2 代码实现

3. A星寻路算法

4. 红包算法

4.1 二倍均值法

4.2 线段切割法

---

1. Bitmap的巧用

Bitmap算法，又叫做位图算法，这里所说的位图并不是像素图片的位图，而是内存中连续的二进制位所组成的数据结构，该算法主要用于对大量整数做去重和查询操作。

1.1 查询

举个例子，假设给出一块长度为10bit的内存空间，也就是Bitmap，想要依次插入证书4、1、2、3，需要怎么做？

• 第1步：给出一块长度为10的Bitmap，其中的每一个bit位分别对应着从0到9的整型数。此时，Bitmap的所有位都是0；
• 第2步：把整型数4存入Bitmap，对应存储的位置就是下标为4的位置，将此bit设置为1；
• 第3步：类似第2步；
• 第4步：类似第2步；
• 第5步：类似第2步。

如果问此时Bitmap里存储了哪些元素，显然是4、3、2、1，一目了然。

1.2 去重

例如用Bitmap的形式存储用户标签，以标签为中心，一个标签对应多个用户，例如用户信息：

ID	Name	Sex	Age	Occupation	Phone
1	小灰	男	90后	程序员	苹果
2	大黄	男	90后	程序员	三星
3	小白	女	00后	学生	小米

 

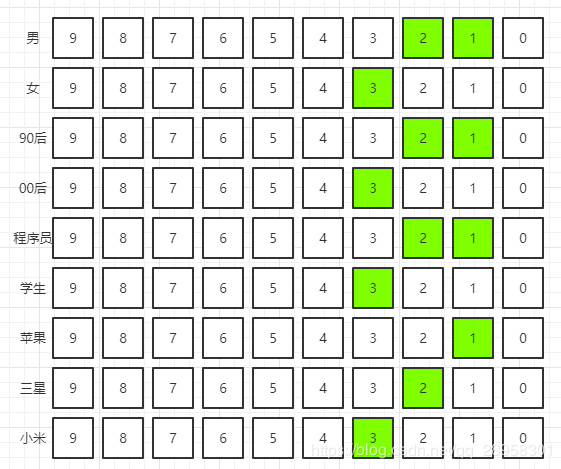
让每一个标签存储包含此标签的所有用户ID，每一个标签都是一个独立的Bitmap：

Sex	Bitmap
男	1, 2
女	3

Age	Bitmap
90后	1, 2
00后	3

Occupation	Bitmap
程序员	1, 2
学生	3

Phone	Bitmap
苹果	1
三星	2
小米	3

 

这样一来，每一个用户特征都变得一目了然：

• 查找使用苹果手机的程序员用户：

0000000010B & 0000000110B = 0000000010B，只有ID为1的用户。

• 查找所有男性用户或00后用户：

0000000110B | 0000001000B = 0000001110B，包括ID为1、2、3的用户。

• 查找非90后的用户：

90后用户：0000000110B

全量用户（90后用户+00后用户）：0000001110B

90后用户与全量用户作异或运算：

0000000110B ^ 0000001110B = 0000003000B

1.3 Bitmap的代码实现

public class MyBitmap {

    private long[] words;
    private int size;

    public MyBitmap(int size) {
        this.size = size;
        this.words = new long[getWordIndex(size - 1) + 1];
    }

    /**
     * 定位Bitmap某一位所对应的word
     * @param bitIndex
     * @return
     */
    private int getWordIndex(int bitIndex) {
        return bitIndex >> 6;
    }

    /**
     * 把Bitmap某一位设置为true
     * @param bitIndex
     */
    public void setBit(int bitIndex) {
        if (bitIndex < 0 || bitIndex > size - 1) {
            throw new IndexOutOfBoundsException("超过Bitmap有效范围");
        }
        int wordIndex = getWordIndex(bitIndex);
        words[wordIndex] |= (1L << bitIndex);
    }

    /**
     * 判断Bitmap某一位的状态
     * @param bitIndex
     * @return
     */
    public boolean getBit(int bitIndex) {
        if (bitIndex < 0 || bitIndex > size - 1) {
            throw new IndexOutOfBoundsException("超过Bitmap有效范围");
        }

        int wordIndex = getWordIndex(bitIndex);
        return (words[wordIndex] & (1L << bitIndex)) != 0;
    }

    public static void main(String[] args) {
        MyBitmap myBitmap = new MyBitmap(128);
        myBitmap.setBit(126);
        myBitmap.setBit(75);
        System.out.println(myBitmap.getBit(126));
        System.out.println(myBitmap.getBit(78));
        
        //Java的实现类
        BitSet bitSet = new BitSet(128);
        bitSet.set(126);
        bitSet.set(75);
        System.out.println(bitSet.get(126));
        System.out.println(bitSet.get(78));
    }
}

2. LRU算法的应用

LRU就是最近最少使用的意思，是一种内存管理算法，该算法最早应用于Linux操作系统。

这个算法基于：长期不被使用的数据，在未来被用到的几率也不大，因此，当数据所占内存达到一定阈值时，需要移除掉最近最少使用的数据。

2.1 实例问题

比如说现在需要查询用户信息，用户信息当然是存放在数据库里的，但是显然不能每一次请求时都去查询数据库，所以最直观的办法就是在内存中建立一个哈希表用于缓存用户信息，但是长期下来，由于数据增多，可能造成内存溢出，这时候就可以用到LRU算法，将最近最少使用的数据删除。

在LRU算法中，使用的一种数据结构是哈希链表。

2.2 代码实现

public class LRUCache {

    private class Node {
        public Node pre;
        public Node next;
        public String key;
        public String value;

        public Node(String key, String value) {
            this.key = key;
            this.value = value;
        }
    }

    private Node head;
    private Node end;
    private int limit;
    private HashMap hashMap;

    public LRUCache(int limit) {
        this.limit = limit;
        this.hashMap = new HashMap<>();
    }

    private String removeNode(Node node) {
        if (node == head && node == end) {
            //移除唯一节点
            head = null;
            end = null;
        } else if (node == end) {
            //移除尾节点
            end = end.pre;
            end.next = null;
        } else if (node == head) {
            //移除头节点
            head = head.next;
            head.pre = null;
        } else {
            //移除中间节点
            node.pre.next = node.next;
            node.next.pre = node.pre;
        }
        return node.key;
    }

    private void addNode(Node node) {
        if (end != null) {
            end.next = node;
            node.pre = end;
            node.next = null;
        }
        end = node;
        if (head == null) {
            head = node;
        }
    }

    public void put(String key, String value) {
        Node node = hashMap.get(key);
        if (node == null) {
            //key不存在，直接插入最后
            if (hashMap.size() >= limit) {
                //已经满了，移除第一个节点
                hashMap.remove(removeNode(head));
            }
            node = new Node(key, value);
            addNode(node);
            hashMap.put(key, node);
        }
    }

    public String get(String key) {
        Node node = hashMap.get(key);
        if (node == null) {
            //key不存在
            return null;
        }
        if (node != end) {
            //非尾节点移动到最后
            removeNode(node);
            addNode(node);
        }
        return node.value;
    }

    public static void main(String[] args) {
        LRUCache cache = new LRUCache(5);
        cache.put("001", "用户1");
        cache.put("002", "用户2");
        cache.put("003", "用户3");
        cache.put("004", "用户4");
        cache.put("005", "用户5");
        System.out.println(cache.get("002"));
        cache.put("004", "用户4更新");
        cache.put("006", "用户6");
        System.out.println(cache.get("001"));
        System.out.println(cache.get("006"));

        //Java实现类，不同之处在于更新操作也算一次使用
        LinkedHashMap cache1 = new LinkedHashMap(5, 0.75f, true) {
            //超出容量，删除第一个节点，默认是扩容
            @Override
            protected boolean removeEldestEntry(Map.Entry eldest) {
                return size() > 5;
            }
        };
        cache1.put("001", "用户1");
        cache1.put("002", "用户2");
        cache1.put("003", "用户3");
        cache1.put("004", "用户4");
        cache1.put("005", "用户5");
        System.out.println(cache1.get("002"));
        cache1.put("004", "用户4更新");
        cache1.put("006", "用户6");
        System.out.println(cache1.get("001"));
        System.out.println(cache1.get("006"));
    }
}

3. A星寻路算法

...

4. 红包算法

4.1 二倍均值法

假设剩余红包金额为m元，剩余人数为n，那么每次抢到的金额 = 随机区间[0.01, m / n * 2 - 0.01]，保证了每次随机金额的平均值是相等的，不会因为抢红包的先后顺序而造成不公平。

这个方法虽然公平，但也存在局限性，即除最后一次外，其他每次抢到的金额都要小于剩余人均金额的2倍，并不是完全自由地随机抢红包。

4.2 线段切割法

把红包总金额想象成一条很长的线段，而每个人抢到的金额，则是这条主线段所拆分出的若干子线段。

当n个人一起抢红包时，就需要确定n-1个切割点。

因此，当n个人一起抢总金额为m的红包时，就需要做n-1次随机运算，以此确定n-1个切割点，随机的范围区间是[1, m-1]。