由于的编辑器不能很好的支持latex,本文中包含latex的部分均为图片,latex文件将会附在末尾。
接下来我们开始利用tensorflow构造一个简单的RNN Basic模型
导入数据
#loading data
import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot = True)
#########################
images = mnist.train.images
labels = mnist.train.labels
images_test = mnist.test.images
labels_test = mnist.test.labels
#####################
设置占位符
x = tf.placeholder(tf.float32, [None, 28, 28])
y = tf.placeholder(tf.float32, [None, 10])
设置参数
batch_size = 256
epochs = 10
num_units = 100
我们只进行10次迭代,用来作为演示。
Basic Cell
basic_cell = tf.keras.layers.SimpleRNNCell(units = num_units)
这里我们只需要输入一个参数,其余参数保持默认即可,如果有兴趣可以转至:
TensorFlow tf.keras.layers.SimpleRNN
虽然是英文,但是都很简单明了。这个语句会帮助初始化所有参量,根据之前的数学背景,所有参量的维度实际上只依赖于num_units, 其余的维度参数将会根据输入数据来调整。
构造 多个basic cell
outputs, states = tf.nn.dynamic_rnn(basic_cell, x, dtype = tf.float32)
这个语句是整个rnn的核心,它会动态地来连接各个basic RNN cell,在我们的例子中,它会连接出28个cells。 另外,这个语句将会返回出两个元素。
在这个程序中,我们一开始输入了batch_size=256 张图片,每个图片包含28个 28*1 的列向量。
outputs & states
outputs:这个元素中包含了图3中的 所有的输出A(A^{<0>} 除外), 我们可以对output进行softmax来得到所有的预测值Y(这个例子里面不需要,因为我们在处理的是一个 many to one 的问题,我们仅仅需要最终的一个结果,而不需要在每个时间step上面做输出)维度自然为(batch_size = 256, steps = 28, num_units = 100)
states:这个元素仅仅包含了图3中的 (A^{
multi-layer case
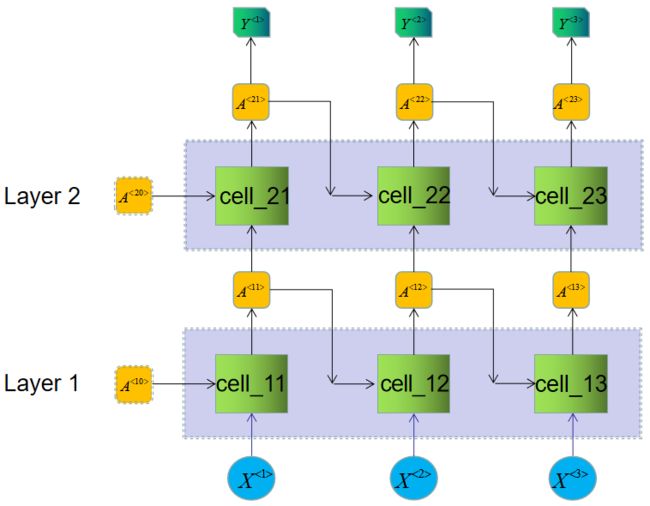
之前,我们仅仅讨论的是最为简单的case, 是一个单层的RNN模型, 为了更加方便的理解整个outputs&states, 我们这里插入一段 multilayer RNN 的case。
在这个case下:
outputs: 维度(batch_size = 256, steps = 28, num_units = 100)因为只包含了每个step上面最后一层的输出,因此就算是multilayer 也不影响它的维度。
states:维度( batch_size = 256, layers = 2, num_units = 100)因为包含了每一层最后一个step的输出,因此在multiplayer下面,维度会变化, 即包含了 (A^{<13>}, A^{<23>})。
FC layer
由于我们的问题是一个many to one 的case, 一张图片, 28个输入, 我们只需要最终一个输出,因此,我们只需要states这个参量, 对其进行FC 映射到一个 10*1 的列向量(对应0~9)
logits = tf.contrib.layers.fully_connected(states, 10, activation_fn = None)
loss and optimizer
这部分就是普通的softmax以及Adam(Adam参数全部默认)
loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits = logits, labels = y))
optimizer = tf.train.AdamOptimizer().minimize(loss)
精度检验
correct_predict = tf.equal(tf.argmax(logits, 1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_predict, tf.float32))
开始训练
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for epoch in range(epochs + 1):
for _ in range(mnist.train.num_examples // batch_size):
x_batch, y_batch = mnist.train.next_batch(batch_size)
x_batch = x_batch.reshape([-1, 28, 28])
sess.run(optimizer, feed_dict = {x: x_batch, y: y_batch})
acc_train = sess.run(accuracy, feed_dict = {x: x_batch, y : y_batch})
acc_test = sess.run(accuracy, feed_dict = {x: images_test, y: labels_test})
print(epoch, "acc_train = ", acc_train, "acc_test = ", acc_test)
注释:
在上面的语句中
x_batch = x_batch.reshape([-1, 28, 28])
我们用reshape将输入转换成方阵, 维度定义为 (batch_size, time_steps, num_inputs)
程序结果
0 acc_train = 0.96875 acc_test = 0.934
1 acc_train = 0.9921875 acc_test = 0.9412
2 acc_train = 0.96875 acc_test = 0.9533
3 acc_train = 0.96875 acc_test = 0.9583
4 acc_train = 0.9453125 acc_test = 0.963
5 acc_train = 0.9921875 acc_test = 0.963
6 acc_train = 0.9765625 acc_test = 0.965
7 acc_train = 0.984375 acc_test = 0.9609
8 acc_train = 0.984375 acc_test = 0.9717
9 acc_train = 0.96875 acc_test = 0.9675
10 acc_train = 0.984375 acc_test = 0.9733
11 acc_train = 0.9765625 acc_test = 0.9615
12 acc_train = 1.0 acc_test = 0.9713
13 acc_train = 0.984375 acc_test = 0.9692
14 acc_train = 0.984375 acc_test = 0.9746
15 acc_train = 0.9609375 acc_test = 0.9747
16 acc_train = 0.984375 acc_test = 0.9737
17 acc_train = 0.9921875 acc_test = 0.9732
18 acc_train = 0.96875 acc_test = 0.9704
19 acc_train = 0.984375 acc_test = 0.9742
20 acc_train = 0.9765625 acc_test = 0.9711
Latex 源码
\documentclass[10pt]{ctexart}
\pagenumbering{gobble}
\usepackage[utf8]{inputenc}
\usepackage{hyphsubst}
\HyphSubstLet{english}{usenglishmax}
\usepackage[english]{babel}
\usepackage{amsthm}
\usepackage{listings}
\usepackage{amsfonts}
\usepackage{mathrsfs}
\usepackage{mathtools}
\usepackage{romannum}
\usepackage{relsize}
\usepackage{hyperref}
\usepackage{empheq}
\usepackage{booktabs}
\usepackage[usestackEOL]{stackengine}
\usepackage{amssymb}
\usepackage{amsmath}
\usepackage{eucal}
\usepackage[usenames, dvipsnames]{color}
\usepackage{romannum}
\usepackage{graphicx}
\usepackage{tikz}
\usepackage{tikz-cd}
\usepackage{graphicx}
\usepackage{wasysym}
\usetikzlibrary{arrows}
%--------------------------------------------%
%\pagestyle{empty}
\setlength\parskip{\medskipamount}
\setlength\parindent{0pt}
%\setlength{\topmargin}{-0in}
%\setlength{\headheight}{0in}
%\setlength{\headsep}{0in}
%\setlength{\footskip}{0in}
\setlength{\evensidemargin}{0in}
\setlength{\oddsidemargin}{0.5in}
%\setlength{\textheight}{9in}
\setlength{\textwidth}{6in}
%--------------------------------------------%
\DeclareMathOperator{\Ker}{Ker}
%--------------------------------------------%
\theoremstyle{definition}
\newtheorem{definition}{Definition}[section]
\newtheorem*{remark}{Remark}
\newtheorem{theorem}{Theorem}[section]
\newtheorem{corollary}{Corollary}[theorem]
\newtheorem{prop}[theorem]{Proposition}
\newtheorem{lemma}[theorem]{Lemma}
%--------------------------------------------%
\newcounter{problem}
\newcounter{solution}
\newcommand\Problem{%
\stepcounter{problem}%
\textbf{\theproblem.}~%
\setcounter{solution}{0}%
}
\newcommand\TheSolution{%
\textbf{Solution:}\\%
}
\newcommand\ASolution{%
\stepcounter{solution}%
\textbf{Solution \thesolution:}\\%
}
\parindent 0in
\parskip 1em
\newcommand*\widefbox[1]{\fbox{\hspace{2em}#1\hspace{2em}}}
%--------------------------------------------%
\newcommand*{\vimage}[1]{\vcenter{\hbox{\includegraphics{#1}}}}
\newcommand*{\vpointer}{\vcenter{\hbox{\scalebox{2}{\Huge\pointer}}}}
\newcommand{\dis}{\displaystyle}
\newcommand{\supp}{\text{Supp}}
\newcommand{\zzz}{\mathbb Z}
\newcommand{\ric}{\text{Ric}}
\newcommand{\kkk}{\mathbb K}
\newcommand{\ccc}{\mathbb C}
\newcommand{\fff}{\mathbb F}
\newcommand{\rrr}{\mathbb R}
\newcommand{\bbb}{\mathbb B}
\newcommand{\nnn}{\mathbb N}
\newcommand{\sss}{\mathbb S}
\newcommand{\ooo}{\mathcal O}
\newcommand{\ee}{\mathcal{E}}
\newcommand{\dd}{\mathcal{D}}
\newcommand{\bb}{\mathfrak{b}}
\newcommand{\pp}{\mathfrak{p}}
\newcommand{\qq}{\mathfrak{q}}
\newcommand{\mm}{\mathfrak{m}}
\newcommand{\nn}{\mathfrak{n}}
\newcommand{\norm[1]}{\left\lVert#1\right\rVert}
\newcommand{\overbar}[1]{\mkern 1.5mu\overline{\mkern-1.5mu#1\mkern-1.5mu}\mkern 1.5mu}
\newcommand{\divides}{\bigm|}
\newcommand{\ndivides}{%
\mathrel{\mkern.5mu % small adjustment
% superimpose \nmid to \big|
\ooalign{\hidewidth$\big|$\hidewidth\cr$\nmid$\cr}%
}%
}
\newcommand{\pa}{\partial}
%--------------VECTOR ARROW------------------%
\usepackage{kpfonts}
\usepackage{stackengine}
\usepackage{calc}
\newlength\shlength
\newcommand\xshlongvec[2][0]{\setlength\shlength{#1pt}%
\stackengine{-5.6pt}{$#2$}{\smash{$\kern\shlength%
\stackengine{7.55pt}{$\mathchar"017E$}%
{\rule{\widthof{$#2$}}{.57pt}\kern.4pt}{O}{r}{F}{F}{L}\kern-\shlength$}}%
{O}{c}{F}{T}{S}}
%--------------------------------------------%
%\[
%\left\{
%\begin{array}{ll}
%\end{array} \right.
%\]
%--------------------------------------------%
%--------------------------------------------%
%\begin{center}
%\begin{tikzpicture}
%\matrix (m) [matrix of math nodes,row sep=3em,column sep=4em,minimum width=2em]
%{M & N & 0\\
%&P \\
%S &F(s)\\};
%\path
%(m-1-1) edge [-stealth] node [above] {$\varphi$} (m-1-2)
%(m-1-2) edge [-stealth] node [above] {$ $} (m-1-3)
%(m-2-2) edge [-stealth] node [left] {$f$} (m-1-2)
%(m-3-2) edge [-stealth] node [left] {$\pi$} (m-2-2)
%(m-3-1) edge [-stealth] node [above] {$\iota$} (m-3-2)
%(m-3-2) edge [-stealth] node [left] {$F'$} (m-1-1)
%(m-2-2) edge [-stealth] node [right] {$F$} (m-1-1)
%(m-3-1) edge [-stealth] node [left] {$ $} (m-1-1)
%;
%\end{tikzpicture}
%\end{center}
%--------------------------------------------%
%\includegraphics{picturename.png}
%--------------------------------------------%
\title{Machine Learning}
\begin{document}
\maketitle
\section{数学符号}
\begin{itemize}
\item 在这篇文章中,我们将一个行向量表示成 $1 \times n$ 的矩阵
\item 在这篇文章中,我们将一个列向量表示成 $m \times 1$ 的矩阵
\end{itemize}
以上说明是为了明确一点,对于给定维度$[m,n]$的矩阵,第一个数字表示行数。(在很多机器学习的笔记中,有可能出现相反的定义,所以在文章开头先做解释)
\begin{itemize}
\item $X^{}_i$ 表示第k个数据输入中的第i个元素。
\item $A^{}_i$ 表示第k个数据输出中的第i个元素。
\item $Y^{}_i$ 表示第k个预测输出中的第i个元素。
\item $B$ bias
\item $W^{}$ variable matrix w.r.t $X^{}$
\end{itemize}
\section{MNIST}
我们这里不再赘述这个数据集。 对于这个数据集里面的图片,我们拿到的将会是一个 $784 \times 1$的列向量, 它代表着一个像素为$28 \times 28$的灰度图片。 如果我们想要利用MLP来对这个数据集进行拟合,那么并不需要对数据集进行转换。 如果我们要利用CNN 或是RNN来进行拟合的话,则需要用reshape命令将其还原至$28 \times 28$的方阵。
\section{MLP}
最基本的RNN算法实际上是一种特殊的MLP。我们先简单回顾一下MLP算法。
如下图所示:
\begin{center}
\includegraphics[width = 10cm]{pic/MLP.png}
\end{center}
我们将一个 $5 \time 1$的矩阵输入,令变量 $M$为一个 $4 \times 5$的矩阵,$B$ 为bias,则
$$A = MX + B$$
我们的到输出A, A 是一个 $4 \times 1$ 的矩阵。 最后在通过一些激活函数或是再增加一个W矩阵得到最终的预测值$\hat{Y}$. 本质上这是一种线性回归模型。
\newpage
\section{RNN Basic}
在上一小节中,我们简单回顾了MLP。 在这类算法中,我们实际上将数据集中的各个数据视为相对独立,并不互相干扰,尽管他们共用了矩阵M以及bias B。但是在实际生活中,数据之间并不相互独立, 例如在中文联想中,上下文的语境关系往往是最为重要的。RNN可以很好的解决这类问题,我们将通过tensorflow代码与数学原理的结合来介绍这个算法。\\
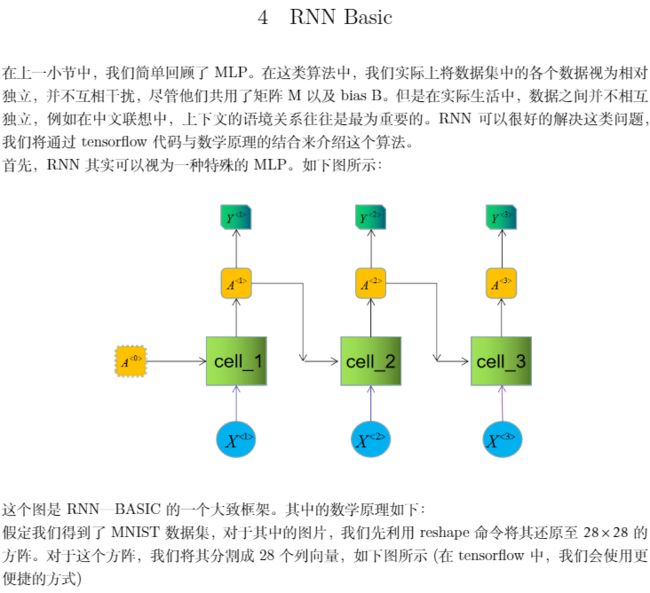
首先,RNN其实可以视为一种特殊的MLP。 如下图所示:
\begin{center}
\includegraphics[width = 10cm]{pic/Rnn_01.png}
\end{center}
这个图是RNN—BASIC的一个大致框架。 其中的数学原理如下:\\
假定我们得到了MNIST数据集,对于其中的图片,我们先利用reshape命令将其还原至$28 \times 28$的方阵。对于这个方阵,我们将其分割成28个列向量, 如下图所示(在 tensorflow 中,我们会使用更便捷的方式)
\begin{center}
\includegraphics[width = 10cm]{pic/Rnn_02.png}
\end{center}
接着,我们来分析下cell-1里面的数学背景。
\begin{itemize}
\item 对于这个cell来说,它得到了两个输入, 一个是$X^{<1>}$, 另一个是$A^{<0>}$。 由于有两个输入, 我们需要定义两个W矩阵来进行运算, 我们分别定义为$W_{a \rightarrow a}, W_{x \rightarrow a}$.
\item 另外我们还需要定义一个bias, 用B来表示。
\item 第一层的输出计算为:
$$A^{<1>} = \tanh(W_{a \rightarrow a}A^{<0>} + W_{x \rightarrow a}X^{<1>} + B)$$
\item 同理,接下去的计算遵循一样的公式:
$$A^{} = \tanh(W_{a \rightarrow a}A^{} + W_{x \rightarrow a}X^{} + B)$$
\item 所有的cell将会共享两个W矩阵以及一个B矩阵。
\item 对于实际的预测输出,我们可以对输出矩阵A加上激活函数。
\item 我们还需要初始化 $A^{<0>} $, 可以令其为0矩阵。
\end{itemize}
我们回到MNIST 数据集。 对于一张$28 \times 28$的图片, 我们已经分割出28个列向量, 每个列向量的维度为$28 \times 1$.\\
现在我们要引入几个名词(这些名词是在TENSORFLOW语句中使用的)
\begin{itemize}
\item $time\_steps = 28$: 这里我们分割出了28个列向量,意味着我们在时间这一维度有28。 意思是,对于一张图片,我们实际进行了28次的计算,每次计算中只包含一个列向量。
\item $num\_inputs = 28$: 这里我们分割出的列向量为$28 \times 1$, 因此这个参数是28
\item $num\_units = 100$:
这是一个参数,意思是输出A的维数。 回顾到MLP中,A实际上也是一个列向量,我们这里定义A的维度为$num\_units \times 1$。
\item $W_{a \rightarrow a}$ 矩阵的维数应该是$num\_units \times num\_units$, 即 $100 \times 100$, 这样的话, $W_{a \rightarrow a}A^{{k-1}}$ 将会输出一个 $100 \times 1$ 的列向量。
\item $W_{x \rightarrow a}$ 矩阵的维数应该是$num\_units \times num\_inputs$, 即 $100 \times 28$, 这样的话, $W_{a \rightarrow a}X^{{k}}$ 将会输出一个 $100 \times 1$ 的列向量。
\end{itemize}
现在我们可以利用tensorflow来做一个RNN中的cell:\\
\end{document}