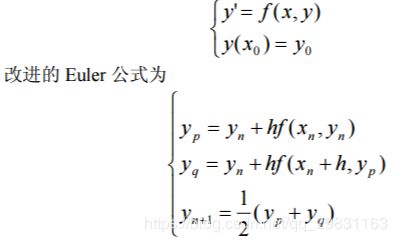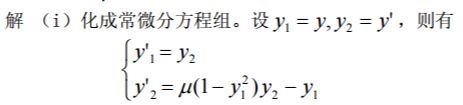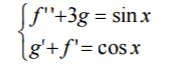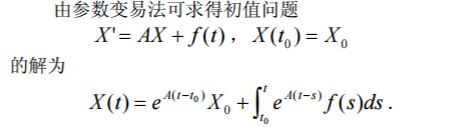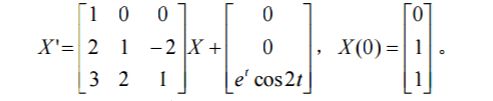常微分方程的解法 (四): Matlab 解法
常微分方程的解法求解系列博文:
常微分方程的解法 (一): 常微分方程的离散化 :差商近似导数、数值积分方法、Taylor 多项式近似
常微分方程的解法 (二): 欧拉(Euler)方法
常微分方程的解法 (三): 龙格—库塔(Runge—Kutta)方法 、线性多步法
常微分方程的解法 (四): Matlab 解法
§7 Matlab 解法
7.1 Matlab 数值解
目录
7.1.1 非刚性常微分方程的解法 (I)对简单的一阶方程的初值问题
7.1.2 刚性常微分方程的解法 7.1.3 高阶微分方程的解法
7.2 常微分方程的解析解
7.2.1 求解常微分方程的通解 7.2.2 求解常微分方程的初边值问题
7.2.3 求解常微分方程组 7.2.4 求解线性常微分方程组
(i)一阶齐次线性微分方程组 (ii)非齐次线性方程组 习 题
7.1.1 非刚性常微分方程的解法
Matlab 的工具箱提供了几个解非刚性常微分方程的功能函数,如 ode45,ode23, ode113,其中 ode45 采用四五阶 RK 方法,是解非刚性常微分方程的首选方法,ode23 采用二三阶 RK 方法,ode113 采用的是多步法,效率一般比 ode45 高。 Matlab 的工具箱中没有 Euler 方法的功能函数。
(I)对简单的一阶方程的初值问题
我们自己编写改进的 Euler 方法函数 eulerpro.m 如下:
function [x,y]=eulerpro(fun,x0,xfinal,y0,n);
if nargin<5,n=50;end
h=(xfinal-x0)/n;
x(1)=x0;y(1)=y0;
for i=1:n
x(i+1)=x(i)+h;
y1=y(i)+h*feval(fun,x(i),y(i));
y2=y(i)+h*feval(fun,x(i+1),y1);
y(i+1)=(y1+y2)/2;
end 例1 用改进的Euler方法求解
解 编写函数文件 doty.m 如下:
function f=doty(x,y);
f=-2*y+2*x^2+2*x; 在Matlab命令窗口输入:
[x,y]=eulerpro('doty',0,0.5,1,10) 即可求得数值解。
(II)ode23,ode45,ode113的使用 Matlab的函数形式是
[t,y]=solver('F',tspan,y0) 这里solver为ode45,ode23,ode113,输入参数 F 是用M文件定义的微分方程 y'= f (x, y) 右端的函数。
tspan=[t0,tfinal]是求解区间,y0是初值。
例2 用RK方法求解
解 同样地编写函数文件 doty.m 如下:
function f=doty(x,y);
f=-2*y+2*x^2+2*x; 在Matlab命令窗口输入:
[x,y]=ode45('doty',0,0.5,1) 即可求得数值解。
7.1.2 刚性常微分方程的解法
Matlab的工具箱提供了几个解刚性常微分方程的功能函数,如ode15s,ode23s, ode23t,ode23tb,这些函数的使用同上述非刚性微分方程的功能函数。
7.1.3 高阶微分方程的解法
(ii)把一阶方程组写成接受两个参数t 和 y ,返回一个列向量的 M 文件 F.m:
function dy=F(t,y);
dy=[y(2);y(3);3*y(3)+y(2)*y(1)]; 注意:尽管不一定用到参数t 和 y ,M—文件必须接受此两参数。这里向量 dy 必须是列 向量。
(iii)用 Matlab 解决此问题的函数形式为
[T,Y]=solver('F',tspan,y0) 这里 solver 为 ode45、ode23、ode113,输入参数 F 是用 M 文件定义的常微分方程组, tspan=[t0 tfinal]是求解区间,y0 是初值列向量。在 Matlab 命令窗口输入 [T,Y]=ode45('F',[0 1],[0;1;-1]) 就得到上述常微分方程的数值解。这里 Y 和时刻 T 是一 一对应的,Y(:,1)是初值问题的 解,Y(:,2)是解的导数,Y(:,3)是解的二阶导数。
例 4 求 van der Pol 方程
的数值解,这里 μ > 0是一参数。
(ii)书写 M 文件(对于 μ =1)vdp1.m:
function dy=vdp1(t,y);
dy=[y(2);(1-y(1)^2)*y(2)-y(1)];(iii)调用 Matlab 函数。对于初值 y(0) = 2, y'(0) = 0 ,解为
[T,Y]=ode45('vdp1',[0 20],[2;0]); (iv)观察结果。利用图形输出解的结果;
plot(T,Y(:,1),'-',T,Y(:,2),'--')
title('Solution of van der Pol Equation,mu=1');
xlabel('time t');
ylabel('solution y');
legend('y1','y2');
例 5 van der Pol 方程, μ =1000 (刚性)
解 (i)书写 M 文件 vdp1000.m:
function dy=vdp1000(t,y);
dy=[y(2);1000*(1-y(1)^2)*y(2)-y(1)];
(ii)观察结果
[t,y]=ode15s('vdp1000',[0 3000],[2;0]);
plot(t,y(:,1),'o')
title('Solution of van der Pol Equation,mu=1000');
xlabel('time t');
ylabel('solution y(:,1)');7.2 常微分方程的解析解
在 Matlab 中,符号运算工具箱提供了功能强大的求解常微分方程的符号运算命令 dsolve。常微分方程在 Matlab 中按如下规定重新表达: 符号 D 表示对变量的求导。Dy 表示对变量 y 求一阶导数,当需要求变量的 n 阶导 数时,用 Dn 表示,D4y 表示对变量 y 求 4 阶导数。 由此,常微分方程 y' '+2y'= y 在 Matlab 中,将写成
D2y+2*Dy=y7.2.1 求解常微分方程的通解
无初边值条件的常微分方程的解就是该方程的通解。其使用格式为:
dsolve('diff_equation') dsolve(' diff_equation','var') 式中 diff_equation 为待解的常微分方程,第 1 种格式将以变量 t 为自变量进行求解, 第 2 种格式则需定义自变量 var。
例 6 试解常微分方程
![]()
解 编写程序如下:
syms x y
diff_equ='x^2+y+(x-2*y)*Dy=0';
dsolve(diff_equ,'x') 7.2.2 求解常微分方程的初边值问题
求解带有初边值条件的常微分方程的使用格式为:
dsolve('diff_equation','condition1,condition2,…','var') 其中 condition1,condition2,… 即为微分方程的初边值条件。
例 7 试求微分方程
解 编写程序如下:
y=dsolve('D3y-D2y=x','y(1)=8,Dy(1)=7,D2y(2)=4','x')7.2.3 求解常微分方程组
求解常微分方程组的命令格式为:
dsolve('diff_equ1,diff_equ2,…','var')
dsolve('diff_equ1,diff_equ2,…','condition1,condition2,…','var')第 1 种格式用于求解方程组的通解,第 2 种格式可以加上初边值条件,用于具体求解。
例 8 试求常微分方程组:
的通解和在初边值条件为 f '(2) = 0, f (3) = 3, g(5) = 1的解。
解 编写程序如下:
clc,clear
equ1='D2f+3*g=sin(x)';
equ2='Dg+Df=cos(x)';
[general_f,general_g]=dsolve(equ1,equ2,'x')
[f,g]=dsolve(equ1,equ2,'Df(2)=0,f(3)=3,g(5)=1','x') 7.2.4 求解线性常微分方程组
(i)一阶齐次线性微分方程组
例 9 试解初值问题
解 编写程序如下:
syms t
a=[2,1,3;0,2,-1;0,0,2];
x0=[1;2;1];
x=expm(a*t)*x0 (ii)非齐次线性方程组
例 10 试解初值问题
解 编写程序如下:
clc,clear
syms t s
a=[1,0,0;2,1,-2;3,2,1];ft=[0;0;exp(t)*cos(2*t)];
x0=[0;1;1];
x=expm(a*t)*x0+int(expm(a*(t-s))*subs(ft,s),s,0,t);
x=simple(x)习 题
1. 用欧拉方法和龙格—库塔方法求微分方程数值解,画出解的图形,对结果进行 分析比较。
2. 一只小船渡过宽为d 的河流,目标是起点 A 正对着的另一岸 B 点。已知河水 流速 ![]() 与船在静水中的速度
与船在静水中的速度 ![]() 之比为k .
之比为k .
(i)建立小船航线的方程,求其解析解。
(ii)设d = 100 m, 1 v1 = m/s, 2 v2 = m/s,用数值解法求渡河所需时间、任 意时刻小船的位置及航行曲线,作图,并与解析解比较。
常微分方程的解法求解系列博文:
常微分方程的解法 (一): 常微分方程的离散化 :差商近似导数、数值积分方法、Taylor 多项式近似
常微分方程的解法 (二): 欧拉(Euler)方法
常微分方程的解法 (三): 龙格—库塔(Runge—Kutta)方法 、线性多步法
常微分方程的解法 (四): Matlab 解法