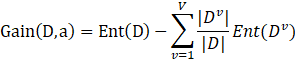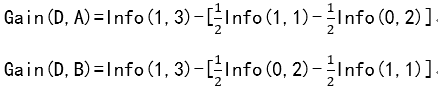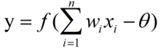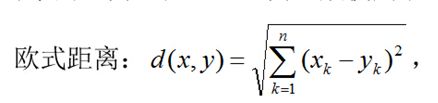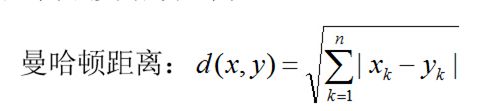人工智能学习笔记（三）---贝叶斯&决策树&感知机算法（神经网络）

目录

一、贝叶斯网络&朴素贝叶斯分类器

二、决策树算法（ID-3）

三、感知机算法（简单的神经网络）

补充概念：Boosting & k-近邻

Boosting

k-近邻（决定待分样本所属类别）

---

一、贝叶斯网络&朴素贝叶斯分类器

贝叶斯网络

参考下图中的贝叶斯网络（见图二），其中布尔变量I=聪明(intelligence)  H=诚实(Honest)  P=受欢迎的(Popular) L=大量的竞选资金  E=竞选成功

(a) 根据该网络结构，是否可以得到P(I,L,H)=P(I)P(L)P(H),如果不是，请给出正确的表达式；

(b)根据该网络结构计算P(i,h,¬l,p,¬e)的值；

(c)假设已知某个人是诚实的，没有大量的竞选资金但是竞选成功了，那么他是聪明的概率是多少？

答：

(a)不是，正确形式：P(I)P(L|H)P(H)   这个表达式表示的是这几个事件同时发生的概率，如果有依赖性则乘的是条件概率

(b)parents(l) = h    parents(p) = i,h,l   parents(e) = p

P(i,h,¬l,p,¬e) = P(i) P(h) P(¬l | h) P(p|i∧h∧¬l) P(¬e|p) = 0.5*0.1*0.7*0.4*0.4 = 5.6×10-3

首先要根据贝叶斯网络确定依赖关系，根据条件概率表获取相应值。

(c)题目要求的条件概率为P(i | h,¬l,e)

P(i | h,¬l,e)= P(i,h,¬l,e) / P(h,¬l,e) = αP(i,h,¬l,e) （α = 1/ P(h,¬l,e)）α代替分母的概率值

αP(i,h,¬l,e)= α[ P(i,h,¬l,e,p) + P(i,h,¬l,e, ¬p) ] = (1.050×10^-2)α      ……①

再计算αP(¬i,h,¬l,e) = α[ P(¬i,h,¬l,e,p) + P(¬i,h,¬l,e, ¬p) ] =  (0.875×10^-2) α ……②

这里用的是P(i | h,¬l,e) + P(¬i | h,¬l,e) = 1得到的

①+② = 1 得 α =  代入①得所要求的概率≈0.545

 

朴素贝叶斯分类器的计算流程

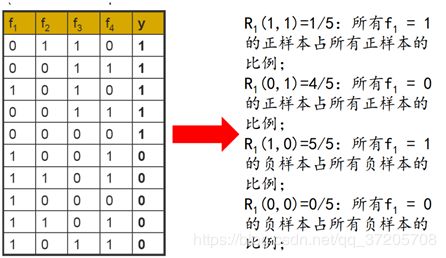
该算法用于将样例进行“正确”地划分，如最终判定为“好”或者“坏”

New x表示一个f1~f4分别为<0,0,1,1>的样本

即计算出正样本中这几个属性同时（独立）拥有的概率

以及负样本中这几个属性同时拥有的概率

比较这两个概率而进行划分

从这个例子中可以看出如果有一个概率为0则最后也为0了，这不太合理，所以有时需要在估计概率的时候进行平滑处理（smoothing），分子+1，分母+N（第i个属性可能的取值数/个数）

 

二、决策树算法（ID-3）

我们希望决策树的分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”（purity）越来越高。”信息熵”（information entropy）是度量样本集合纯度最常用的一种指标。

假定当前样本集合D中第k类样本所占的比例为pk(k=1,2,…,|γ|) ，则D的信息熵定义为

Ent(D)的值越小，则D的纯度越高  （注意负号，算出来为正值）

“信息增益”（information gain）表示为

假定离散属性a有V个可能的取值 ，若使用a来对样本集D进行划分，则会产生V个分支结点，其中第v个分支结点包含了D中所有在属性a上取值为 的样本，记为 。再考虑到不同的分支结点所包含的样本数不同，给分支结点赋予权重 ，即样本数越多的分支结点的影响越大。上式表达的是用属性a（这个属性可能有多种取值）对样本集D进行划分所得到的信息增益。

ID-3决策树学习算法以信息增益为准则来选择划分属性，信息增益越大，意味着用属性a来进行划分所获得的“纯度提升”越大。

扩展：

增益率（gain ratio），信息增益准则对可取值数目较多的属性有所偏好，为减少这种偏好可能带来的不利影响，C4.5使用的是增益率。

剪枝处理：

决策树的基本剪枝策略有“预剪枝（prepruning）”和“后剪枝（post-pruning）”

预剪枝是指在决策树生成过程中，对每个结点在划分前进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点；

后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。

如何判断决策树泛化性能是否提升？

一种方法是预留一部分作为“验证集”……

 

例题：

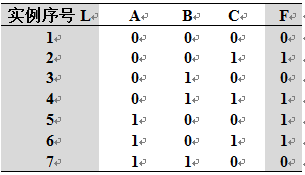
设使用ID3算法(按熵的信息增益标准)进行归纳学习的输入实例集如右下表所示。学习的目标是用属性A、B、C预测属性F（F是目标属性）。

（a）已知Info(x, y) = -(x/(x+y))log(x/(x+y))-(y/(x+y))log(y/(x+y))表示由x个正例和y个反例构成的集合的熵。写出集合S分别以属性A、B、C作为测试属性的熵的增益Gain(S, A)、Gain(S, B)、Gain(S, C)的表达式。

（b）属性A、B、C中哪个应该作为决策树根节点的测试属性？

（c）根据信息理论构造该问题完整的决策树。

Answer:

PS:计算结果有点问题，看表达式就好

(b):C节点的信息增益最大，选择C作为根节点。

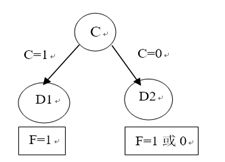
(c):通过C属性，将集合S分为两部分 其中 包含三个正例(F=1), 包含4个实例(一个正例，三个负例)构造如下决策树：

同理，在根据信息理论对 进行分割：

此时，A和B信息增益一样，任选一个构造决策树

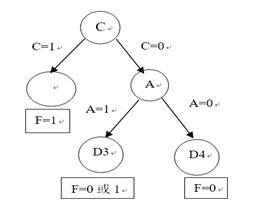
重复这个过程最终得到决策树：

此题答案不唯一，A,B节点的位置可以互换。

 

三、感知机算法（简单的神经网络）

参考：《机器学习》周志华

感知机（Perceptron）由两层神经元组成，输入层接收外界输入信号后传递给输出层，输出层是M-P神经元，亦成“阈值逻辑单元”（threshold logic unit）

M-P神经元模型

感知机学习过程：

给定训练数据集，通过学习得到权重wi=1,2,…,n 以及阈值θ。阈值θ可看作一个固定输入为-1.0的“哑结点”（dummy node）所对应的连接权重wn+1 （它对应的xi一直为-1），这样，权值和阈值的学习就可统一为权重的学习。

对训练样例（x,y），若当前感知机的输出为 ，则感知机权重将这样调整：

其中xi是x对应于第i个输入神经元的分量， 是学习率，一般设置为一个小正数。可以看到，若预测正确则权重不作调整，否则将根据错误程度进行权重调整。

另外，感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元，其只能处理线性可分问题。激活函数是阶跃函数的话大于等于0都输出1.

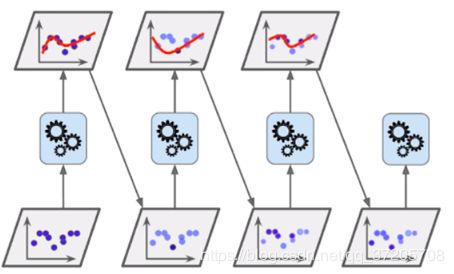
要处理非线性可分问题，需要使用多层功能神经元

描述感知器的学习过程的表如下，下图是And操作感知器的学习过程，题目需要给出初始权值（包括阈值）对每次输入，列出其期待的输出、未更新前的权值、实际输出、错误程度、调整后的权值。

 

补充概念：Boosting & k-近邻

Boosting

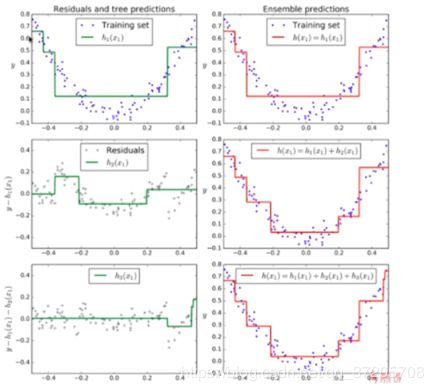
Boosting是集成学习方法中的一类

GradientBoosting是⼀种常⽤的Boosting算法，试析其与AdaBoost的异同。

相同点：都是集成学习，集成多个模型，每个模型都在尝试增强（Boosting）整体的效果；

不同点：

首先分析AdaBoost和GradientBossting各自的特点：

1.AdaBoost每一次生成的子模型都在想办法弥补上一次生成的子模型没有成功预测到的样本点，或者说是弥补上一子模型所犯的错误；也可以说，每一个子模型都在想办法推动（Boosting）整个基础系统，使得整个集成系统准确率更高；

2.每一个子模型都是基于同一数据集的样本点，只是样本点的权重不同（预测错误的点的权重将增加），也就是样本对于每一个子模型的重要程度不同，因此每份子模型也是有差异的；最终以所有子模型综合投票的结果作为 Ada Boosting 模型的最终学习结果；

GradientBoosting:

使用整体的数据集训练第一个子模型 m1，产生错误 e1（m1 模型预测错误的样本数据）；

使用 e1 数据集训练第二个子模型 m2，产生错误 e2；

使用 e2 数据集训练第三个子模型 m3，产生错误 e3；

……

最终的预测结果是：m1 + m2 + m3  +  ……     回归问题

其特点如下：

1.每一个模型都是对前一个模型所犯错误的补偿；

2.Gradient Boosting 集成学习算法不能对基本算法进行选择，它的的基本算法就是决策树算法；

下面可以作出结论：

1.AdaBoost与Gradient Boosting在数据集的选择方式上不同，

AdaBoost的后面的模型与前面的共用同一数据集，只是每次的预测结果将改变数据点在下一个模型中的权重，而Gradient Boosting的后面的模型的数据集为前一模型的错误预测的样本数据。

2.各模型算法的选择方式不同

AdaBoost不同模型可以选择不同的基本算法，而Gradient Boosting各模型只采用决策树算法。

 

k-近邻（决定待分样本所属类别）

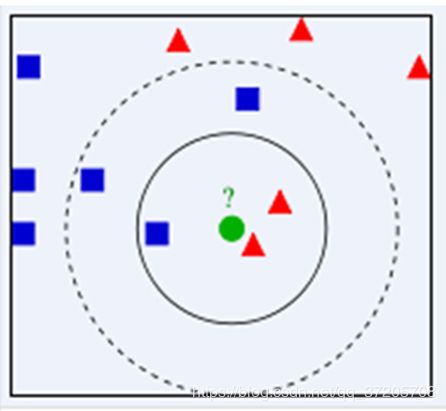
KNN邻近算法是通过测量不同特征值之间的距离进行分类。

    它的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中K通常是不大于20的整数。

     KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

归一化：

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

   其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。

 

举个例子：

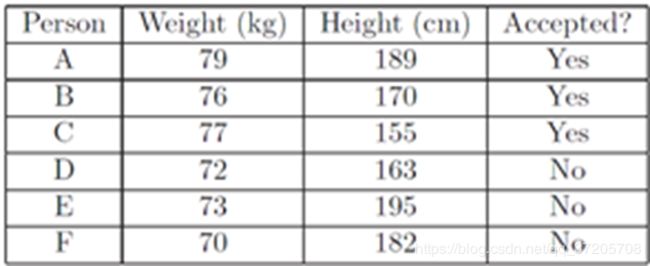
阿蕉是一位健身爱好者。有一天他想去一家健身俱乐部应聘健身教练。但是这家俱乐部有身高和体重的要求，于是阿蕉找来了面试过这家俱乐部的人员名单，如下

                

在KNN中，通过计算对象间距离来作为各个对象之间的非相似性指标，避免了对象之间的匹配问题，在这里距离一般使用欧氏距离或曼哈顿距离

             

算法思想

1）计算测试数据与各个训练数据之间的特征欧式距离；

2）按照距离的递增关系进行排序；

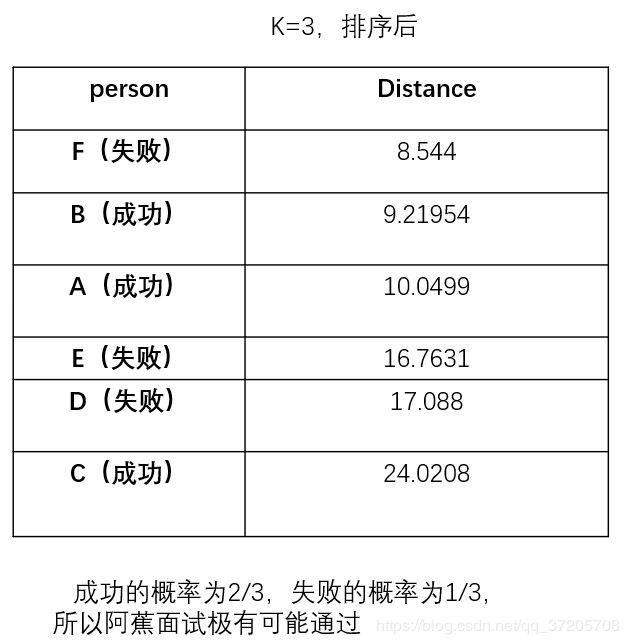
3）选取距离最小的K个点；

4）确定前K个点所在类别的出现频率；

5）返回前K个点中出现频率最高的类别作为测试数据的预测分类。

 

我们把体重和身高作为欧式平面的两个维度，把所有人作为拥有两个坐标的点描述在平面上。计算阿蕉与其他人的欧式距离，如图（x、y视为身高和体重）

                      

仅仅改变了k结果却不一样了，这是不符合我们的期望的。（某个属性可能拉大距离）

数据的标准化（normalization）是将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

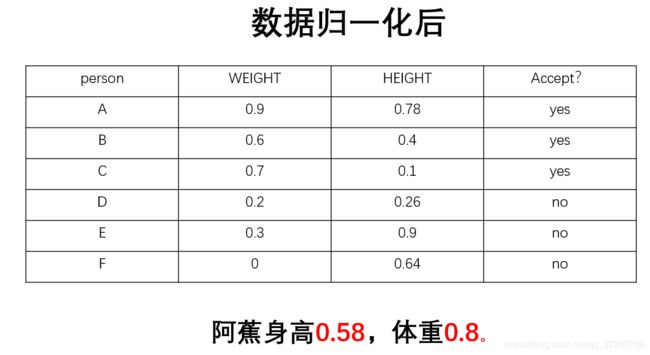
其中最典型的就是数据的归一化处理，即将数据统一映射到[0,1]区间上。处理公式如下

W=(w-70)/10.

H=(h-150)/50.

数据归一化的好处

1.提升模型的精度，让各个特征对结果做出的贡献相同，可以大大提高分类器的准确性

2.提升模型的收敛速度，例如在某些算法中可以让梯度下降的速度加快，避免训练模型的时间过长

 

END