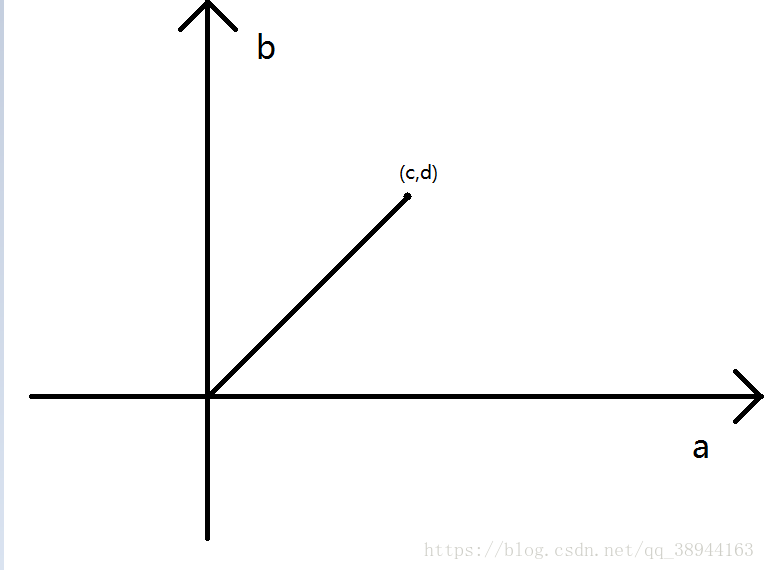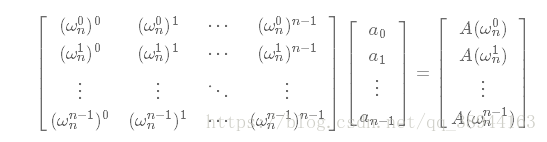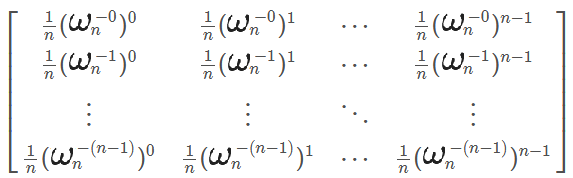浅谈 FFT (终于懂一点了~~)
FFT(离散傅氏变换的快速算法)
FFT(Fast Fourier Transformation)是离散傅氏变换(DFT)的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性,对离散傅立叶变换的算法进行改进获得的。
以上内容摘自百度百科,其实看了等于没看
首先先要知道一些预备知识:
1、多(door♂)项式
2、复数的运算(不是负数)
3、下面开始讲吧……
首先,多(door♂)项式是蛤?
![]()
也可表示为![]()
这个就是多项式,一般是吧高次项写在前面,我这里这样写只是为了方便。
那么FFT是用来干蛤的?
这个问题问得好,FFT是用来算两个多项式相乘的。
那不可以暴力乘吗(![]() )?
)?
那暴力可以做到 ![]() 吗?
吗?
。。。。
---------------------------------------------------------------------------------先分个鸽-------------------------------------------------------------------------------------
首先先要有复数运算的知识
我们知道 ![]() (
(![]() 是个虚数)
是个虚数)
那么对于形如![]() ,其中a,b为实数,i为虚数的东东我们称它为复数
,其中a,b为实数,i为虚数的东东我们称它为复数
a 为实部,bi为虚部。
加法运算: 实部+实部 虚部+虚部
减法运算:同上,‘+’ —> ‘-’
乘法运算:就和正常的多项式乘法差不多,只不过要注意 ![]()
除法运算:分数上下同时乘分母的共轭
即:
一个复数共轭就是一个实部相同,虚部为相反数的复数
如![]() 的共轭是
的共轭是![]()
一个复数![]() 的共轭通常表示为
的共轭通常表示为![]()
可得
因为![]() 所以分母必定为实数
所以分母必定为实数
对于 ![]() 我们还可以这样子表示
我们还可以这样子表示
其中a为实轴,b为虚轴,![]() 就可以表示为在这样一个二维平面上的一个点
就可以表示为在这样一个二维平面上的一个点
复数乘法在平面中就是辐角相加,模长相乘 (这个用三角函数可以证明,这里就不多说了)
真香
证明:对于![]() 可以表示为
可以表示为![]() 其中
其中![]() 为辐角,
为辐角,![]() 为半径(即模长),然后相乘就直接r相乘指数相加就行了
为半径(即模长),然后相乘就直接r相乘指数相加就行了
-----------------------------------------------------------------------------再次分鸽----------------------------------------------------------------------------------
下面重点来辣!重点警告!!重点警告!!重点警告!!(重要的事情说三遍(滑稽
嗯哼。。。。好了继续
然后是一个很重要的东西
单位根
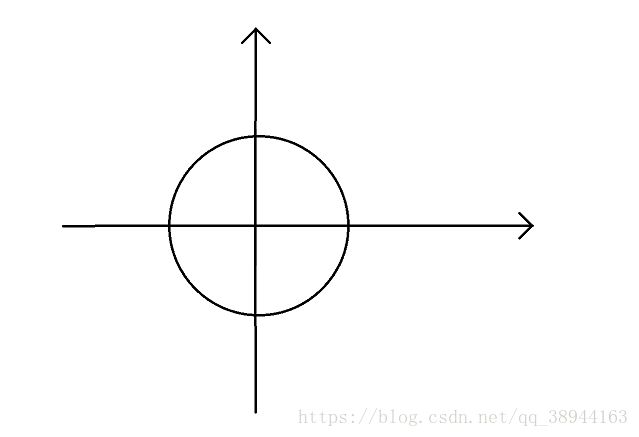
首先这是个圆(废话),它的半径是一,所以称为单位圆
复数满足![]()
![]() 称
称![]() 作是
作是![]() 次单位根
次单位根
在平面上表示的话……算了吧
真香
即将圆等分成3份
n次单位根就是将单位圆等分成n份
一下记第k个n次单位根为![]() (从1开始,逆时针第k+1个为
(从1开始,逆时针第k+1个为![]() )
)
单位根的特殊性质可以保证![]() 这n-1个复数各不相等
这n-1个复数各不相等
单位根还有一些性质:
![]()
![]()
(高清无码)
这两条性质带进下面的欧拉公式就可以算出来了
对了忘记说![]() 怎么算了,用我们强dark的欧拉公式可以解决:
怎么算了,用我们强dark的欧拉公式可以解决:
欧拉公式:![]()
因为c++是用弧度制所以我下面也用弧度制表示(即![]() 表示
表示![]() ,
,![]() 表示
表示![]() )
)
-----------------------------------------------------------------------------------分鸽------------------------------------------------------------------------------------
现在可以开始讲 了
了
![]() (当当当当)
(当当当当)
还记得这个东东吗,不过这只是多项式的一种表达方式,叫作:系数表达法
还有种表达法叫:
点值表达法
设![]()
![]()
我们知道,n+1个互不相同的点![]() 就可以确定一个n次函数,对
就可以确定一个n次函数,对![]() 分别求值就可以得到
分别求值就可以得到![]() ,那么称
,那么称![]() 为door项式的点表示法
为door项式的点表示法
---------------------------------------------------------------------------啦啦啦啦啦啦啦啦(还是分鸽)-----------------------------------------------------------
为蛤要用点值表示法呢?
因为我们![]() 现,系数表示法算多项式乘法的时间复杂度是
现,系数表示法算多项式乘法的时间复杂度是![]() ,而通过点值表示法我们可以发现两个多项式
,而通过点值表示法我们可以发现两个多项式![]() ,同时取点
,同时取点![]() 时,得到的是
时,得到的是![]() 和
和![]() ,即取到的点分别为
,即取到的点分别为![]() 而
而![]() 会取到的点为
会取到的点为![]()
(显而易见)。那么计算![]() 的点表达式的时间复杂度就是
的点表达式的时间复杂度就是![]() 的。
的。
我知道了o(*^▽^*)┛,就是把值直接带进去,然后就可以线性求出来了,干嘛要![]() 啊?
啊?
但是……你要带![]() 个值进去才可以弄出点表示法呀。
个值进去才可以弄出点表示法呀。
.........那不还是![]() 的吗,哪来的
的吗,哪来的![]() ...
...
![]() 有办法让这个过程变成
有办法让这个过程变成![]() ,别急,马上就要讲了。
,别急,马上就要讲了。
-------------------------------------------------------------------------分鸽(下面就不解释了)------------------------------------------------------------------------
FFT就是将系数表示法转化成点值表示法相乘,再由点值表示法转化为系数表示法的过程,第一个过程叫做求值(DFT),第二个过程叫做插值(IDFT)——摘自一位darklao的blog
首先是求值DFT
![]()
![]()
(高清无码++)
再次把单位根的性质搬出来。。
想要求出一个多项式的点值表示法,需要选出![]() 个数分别带入到多项式里面,带入一个数的复杂度是
个数分别带入到多项式里面,带入一个数的复杂度是![]() 的,那么总复杂度就是
的,那么总复杂度就是![]() 的,因为单位根有上面两个优美的性质,所以我们尝试可以取
的,因为单位根有上面两个优美的性质,所以我们尝试可以取![]() 次单位根组成
次单位根组成![]() ,看看能不能加速我们的运算....
,看看能不能加速我们的运算....
设![]() 为X的指数为偶数次的,
为X的指数为偶数次的,![]() 为X的指数为奇数次的
为X的指数为奇数次的
可得
![]()
![]() (这里n为2^k,不够就补齐,反正系数为0,不影响)
(这里n为2^k,不够就补齐,反正系数为0,不影响)
![]() 然后我们发现
然后我们发现![]() 和
和![]() 是两个长度为原来一半的多项式,然后就可以分治了
是两个长度为原来一半的多项式,然后就可以分治了
把单位根带进去
![]()
由上面的性质可化简得
![]()
![]() 和
和![]() 递归进去算就行了,然后
递归进去算就行了,然后![]() 就先把
就先把![]() 算出来,然后k次幂就行了
算出来,然后k次幂就行了
先把式子列出来
![]()
用上面的性质化简一下就变成
![]()
然后就可以愉快地把系数表达式转换为点值表达式
||||||好了,求值(DFT)搞定了,下面是插值。||||||
-------------------------------------------------------------分鸽线(真香*2)--------------------------------------------------------------------
插值只要将所有的![]() 变成
变成![]() ,就是将虚部取反,再将结果除以长度(即n),至于为甚,我们可以这样考虑。
,就是将虚部取反,再将结果除以长度(即n),至于为甚,我们可以这样考虑。
我们可以考虑把原来的要做的操作用矩阵的形式表现出来:
这是DFT,我们要求的IDFT,我们已知了左边和右边的两个矩阵,要求中间那个,就相当于是求最左边那个矩阵的逆,然后乘右边那个矩阵。它的逆就是
这个手推一下就行了,![]() 是因为带入了n个值。然后发现IDFT和DFT差不多
是因为带入了n个值。然后发现IDFT和DFT差不多
(下面的推导要用到 ![]() 和
和 ![]() )
)
![]()
![]()
然后就可以了。
真香……
递归的写法:
#include
#define N 8000005
using namespace std;
const double pi = acos(-1.0);
const double eps = 1e-6;
struct complexx{
double x, y;
complexx(double xx = 0, double yy = 0) {x = xx, y = yy;}
}a[N], b[N];
complexx operator + (complexx a, complexx b) {return complexx(a.x + b.x, a.y + b.y);}
complexx operator - (complexx a, complexx b) {return complexx(a.x - b.x, a.y - b.y);}
complexx operator * (complexx a, complexx b) {return complexx(a.x * b.x - a.y * b.y, a.y * b.x + a.x * b.y);}
void fft(int len, complexx *a, int o){
if(len == 1) return;
complexx a0[(len >> 1) + 3], a1[(len >> 1) + 3];
for(int i = 0; i <= len; i += 2)
a0[i >> 1] = a[i], a1[i >> 1] = a[i + 1];
fft(len >> 1, a0, o);
fft(len >> 1, a1, o);
complexx wn = complexx(cos(2 * pi / len), o * sin(2 * pi / len)), w0 = complexx(1, 0);
for(int i = 0; i < (len >> 1); i ++, w0 = w0 * wn){
a[i] = a0[i] + w0 * a1[i];
a[i + (len >> 1)] = a0[i] - w0 * a1[i];
}
}
int n, m;
int main(){
scanf("%d%d", &n, &m);
for(int i = 0; i <= n; i ++) scanf("%lf", &a[i].x);
for(int i = 0; i <= m; i ++) scanf("%lf", &b[i].x);
int len = 1;
for(;len <= n + m; len <<= 1);
fft(len, a, 1);//DFT
fft(len, b, 1);//DFT
for(int i = 0; i <= len; i ++)
a[i] = a[i] * b[i];
fft(len, a, -1);//IDFT
for(int i = 0; i <= n + m; i ++) printf("%.0f ", a[i].x / len + eps);//记得除len
return 0;
} ----------------------------------------------------------------------------分个鸽(真香)--------------------------------------------------------------------
当然,递归的写法常数巨dark,于是乎就有了非递归即迭代的写法。
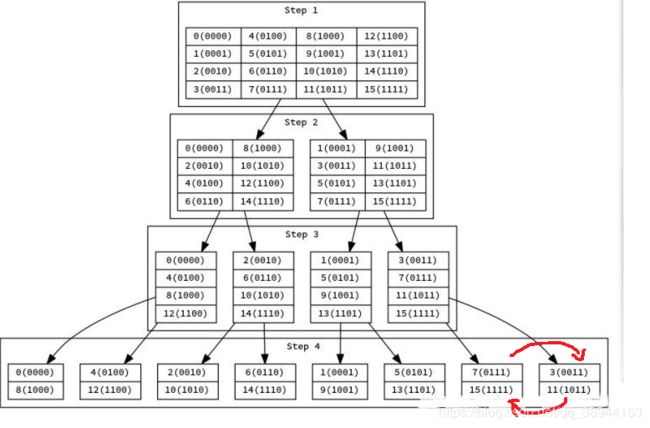
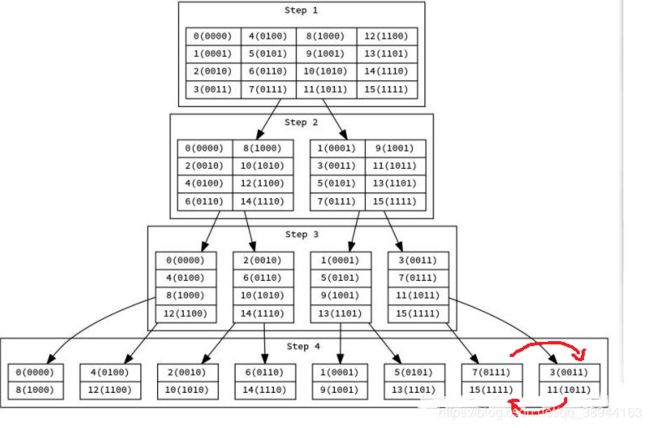
先盗个图
当我们做递归版的FFT的时候,在第i层就相当于把当前数的二进制第i位为零的分一类,为一的分一类,然后分别递归进去。
再偷一张图
注意这副图的原图最后两个地方放反了
现在应该清楚很door了吧。
那么代码:(待填坑……)
等等(update 2019.4.9)
时隔将近一年,终于来填坑了,看看之前写的,感觉初一的时候还是太菜(现在还是很菜)。
emmmmmm……
讲一蛤fft的优化吧
首先看之前的代码,发现算三角函数的那部分被重复调用了很多次,是没有必要的,所以可以先预处理。
设![]() 的实部为
的实部为![]() ,虚部为
,虚部为![]() ,
,
即![]()
由![]()
可得![]()
然后把虚部多除个2就是答案了
code:
#include
#define N 8000005
using namespace std;
const double pi = acos(-1.0);
struct complexx{
double x, y;
complexx(double xx = 0, double yy = 0) {x = xx, y = yy;}
}a[N];
double coss[N], sinn[N];
complexx operator + (complexx a, complexx b) {return complexx(a.x + b.x, a.y + b.y);}
complexx operator - (complexx a, complexx b) {return complexx(a.x - b.x, a.y - b.y);}
complexx operator * (complexx a, complexx b) {return complexx(a.x * b.x - a.y * b.y, a.y * b.x + a.x * b.y);}
void fft(int len, complexx *a, int o){
if(len == 1) return;
complexx a0[(len >> 1) + 3], a1[(len >> 1) + 3];
for(int i = 0; i <= len; i += 2)
a0[i >> 1] = a[i], a1[i >> 1] = a[i + 1];
fft(len >> 1, a0, o);
fft(len >> 1, a1, o);
complexx wn = complexx(coss[len], o * sinn[len]), w0 = complexx(1, 0);
for(int i = 0; i < (len >> 1); i ++, w0 = w0 * wn){
a[i] = a0[i] + w0 * a1[i];
a[i + (len >> 1)] = a0[i] - w0 * a1[i];
}
}
int n, m;
int main(){
scanf("%d%d", &n, &m);
for(int i = 0; i <= n; i ++) scanf("%lf", &a[i].x);
for(int i = 0; i <= m; i ++) scanf("%lf", &a[i].y);
int len = 1;
for(;len <= n + m; len <<= 1);
for(int i = 1; i <= len; i <<= 1) coss[i] = cos(2 * pi / i), sinn[i] = sin(2 * pi / i);//预处理三角函数,只用处理2^k的
fft(len, a, 1);
for(int i = 0; i <= len; i ++)
a[i] = a[i] * a[i];
fft(len, a, -1);
for(int i = 0; i <= n + m; i ++) printf("%.0f ", a[i].y / 2 / len + 0.49);
return 0;
} 好像快了一点,但是仅限如此吗?
现在来填坑了!!!
蝴蝶变换
还是先看这张图
原序列:0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
位逆序置换后:0 8 4 12 2 10 6 14 1 9 5 13 3 11 7 15
然后我们发现了一个神奇的规律,把原序列和置换后的序列的对应位转换为二进制之后是刚好翻转过来的
如1的二进制是0001,8的二进制则是1000,2的二进制是0010,4的二进制是0100,其他也都是如此
证明也十分简单,手推一下就可以了
然后按照置换后的一层一层往上合并就行了
位逆序置换可以用类似数位dp的方法求出来
code:
#include
#define N 8000005
using namespace std;
const double pi = acos(-1.0);
struct complexx{
double x, y;
complexx(double xx = 0, double yy = 0) {x = xx, y = yy;}
}a[N];
double coss[N], sinn[N];
int rev[N];
complexx operator + (complexx a, complexx b) {return complexx(a.x + b.x, a.y + b.y);}
complexx operator - (complexx a, complexx b) {return complexx(a.x - b.x, a.y - b.y);}
complexx operator * (complexx a, complexx b) {return complexx(a.x * b.x - a.y * b.y, a.y * b.x + a.x * b.y);}
void fft(int len, complexx *a, int o){
for(int i = 0; i <= len; i ++) if(i < rev[i]) swap(a[i], a[rev[i]]);
for(int j = 1; j < len; j <<= 1){//j枚举的是合并区间长度的一半,即把两个长度为j的序列合成一个长度为2*j的序列
complexx wn = complexx(coss[j], o * sinn[j]);
for(int k = 0; k < len; k += (j << 1)){//k为当前处理的区间的开头
complexx w0 = complexx(1, 0);
for(int i = 0; i < j; i ++, w0 = w0 * wn){//i为对应位
complexx X = a[i + k], Y = w0 * a[i + j + k];
a[i + k] = X + Y;
a[i + k + j] = X - Y;//合并
}
}
}
}
int n, m;
int main(){
scanf("%d%d", &n, &m);
for(int i = 0; i <= n; i ++) scanf("%lf", &a[i].x);
for(int i = 0; i <= m; i ++) scanf("%lf", &a[i].y);
int len = 1, l = 0;
for(;len <= n + m; len <<= 1, l ++);
for(int i = 0; i <= len; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i&1) << (l - 1));//rev[i]位将i按二进制后的值(类似数位dp的思想)
for(int i = 1; i <= len; i <<= 1) coss[i] = cos(pi / i), sinn[i] = sin(pi / i);//注意这里pi不用乘2
fft(len, a, 1);
for(int i = 0; i <= len; i ++)
a[i] = a[i] * a[i];
fft(len, a, -1);
for(int i = 0; i <= n + m; i ++) printf("%.0f ", a[i].y / 2 / len + 0.49);
return 0;
} FFT的运用!!
前面哔了那么多,可fft除了求多项式乘法还有什么用呢?
没什么用了
因为所有的卷积都可以表示为多项式乘法的形式,所以求卷积的时候之久用fft求就可以了。
卷积
定义:
设 ![]() ,
, ![]() 是两个数列,那么这两个数列的卷积
是两个数列,那么这两个数列的卷积 ![]() 的定义为
的定义为
可以很容易的看出多项式乘法和卷积是类似的
设![]()
![]()
那么![]()
所以遇到要求卷积的时候直接用法法踢就可以了
练习题:https://blog.csdn.net/qq_38944163/article/details/89145308 卷积
https://www.luogu.org/problemnew/show/P1919 多项式乘法
https://www.luogu.org/problemnew/show/P4199万径人踪灭
https://www.luogu.org/problemnew/show/P4173残缺的字符串
https://www.luogu.org/problemnew/show/P3763 [TJOI2017]DNA
https://www.luogu.org/problemnew/show/P3723[AH2017/HNOI2017]礼物
https://www.luogu.org/problemnew/show/P3338[ZJOI2014]力
参考资料:FFT算法讲解——麻麻我终于会FFT了! (通俗易懂,感谢ing)
从多项式乘法到快速傅里叶变换(精准有用,感谢ing)
最后附一句:不要问我是怎么在不用markdown的情况下写下这篇文章的!!!