首先让我们来看Leetcode上的一道题。
Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.
Example 1:
Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.
Example 2:
Input: "cbbd"
Output: "bb"
题意解析:给定一个字符串S,求这个字符串的最长回文子串。所谓回文字符串就是正着读和反着读结果都一样的字符串,如aba,bab。
解法:
(1)暴力求解法:即循环去枚举字符串中的每个字符,这种解法的时间复杂度为O(n^3),再leetcode上应该过不了,所以没有去实现。
(2)中心扩展法:即以某个元素为中心,分别去计算假设回文子串长度为偶数的情况和回文子串长度为奇数的情况下的最长的回文串,这种解法时间复杂度为O(n^2),时间复杂度比第一种算法时间减少了一个指数级,尝试着去实现它,代码如下:
package cn.test.leetcode;
/**
* Created by GavinCee on 2019/5/1.
*/
public class PalindromicStr {
public static void main(String[] args) {
PalindromicStr palindromicStr = new PalindromicStr();
String testStr1 = "babad";
String testStr2 = "cbbd";
String testStr3 = "gabbacg";
String testStr4 = "gabbac";
String testStr5 = "cabbac";
System.out.println(palindromicStr.longestPalindrome(testStr1));
System.out.println(palindromicStr.longestPalindrome(testStr2));
System.out.println(palindromicStr.longestPalindrome(testStr3));
System.out.println(palindromicStr.longestPalindrome(testStr4));
System.out.println(palindromicStr.longestPalindrome(testStr5));
}
public String longestPalindrome(String s) {
if(s == null) {
return null;
}
if(s.equals("")) {
return "";
}
int maxLength = 0;
String result = "";
int len = 1;
if(s.length() > 1) {
len = s.length() - 1;
}
for (int i = 0; i < len; i++) {
String tmp = s.charAt(i) + "";
//1. if the substring length is odd ,so the index is mid.
for(int j = i - 1, k = i + 1;j >=0 && k < s.length(); j--,k++) {
if(s.charAt(j) == s.charAt(k)) {
tmp = s.charAt(j) + tmp + s.charAt(k);
} else {
break;
}
}
if(tmp.length() > maxLength) {
maxLength = tmp.length();
result = new String(tmp);
}
//2' if the substring length is even, the right need plus 2
if (i + 1 < s.length() && s.charAt(i) == s.charAt(i + 1)) {
tmp = s.charAt(i) + "" + s.charAt(i + 1);
for(int j = i - 1, k = i + 2;j >=0 && k < s.length(); j--,k++) {
if(s.charAt(j) == s.charAt(k)) {
tmp = s.charAt(j) + tmp + s.charAt(k);
} else {
break;
}
}
if(tmp.length() > maxLength) {
maxLength = tmp.length();
result = new String(tmp);
}
}
}
return result;
}
}
提交到leetcode后,仍然还是会报时间超时。所以这种解法还被pass掉了。暂时无优化思路,借助百度,了解到还有一种时间复杂度为O(n)的算法,下面强调介绍一下该算法,并顺便整理一下思路。
(3)Manacher算法
Manacher算法提供了一种巧妙的方法,讲长度为奇数的回文串和长度为偶数的回文串一起考虑进来,具体做法是在原字符串的每两个相邻的字符中间插入一个分隔符,同时在原字符串的首尾也都添加上分隔符,该分隔符的要求是不要在原字符串内出现,避免出现混淆。如下所示:
| 原字符串 | 转换后的字符串 |
|---|---|
| babad | #b#a#b#a#d# |
在Manacher算法中用到一个非常重要的辅助数组,我们将转换后的字符串定义为字符数组str[i],其辅助数组定义为len[i]。其中len[i]中的元素为以str[i]为中心时的回文串的最右端字符到str[i]的位置的长度,如下图所示,当i等于3时,str[i]为a,以str[i]为中心的回文串是#b#a#b#,则len[i]为最右字符#到a的长度,即len[i]=4。
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| str[i] | # | b | # | a | # | b | # | a | # | d | # |
| len[i] | 1 | 2 | 1 | 4 | 1 | 4 | 1 | 2 | 1 | 2 | 1 |
该辅助数组len[i]有一个性质,就是len[i] -1就等于该位置所在的字符为中心的原字符串的回文子串的长度。
证明:在转换后的字符串str,因为前后都插入了分隔符,所有的回文子串的长度都是奇数,len[i]为回文最右字符到回文中心的长度,那么对于以str[i]为中心的回文子串的长度就是2*len[i] - 1,算上首尾的分隔符,那么该回文子串会有len[i]个分隔符,所以说原回文子串的长度就是(2len[i] - 1)- len[i] = len[i] - 1。
那么计算最长的回文子串长度,即为计算len[i]数组中的最大值。
假设0<= j <= i,从左往右开始计算len[i],在计算len[i]的时候,由于j<=i,那么在计算len[i]之前len[j]已经计算过了,假设mx为之前计算过的回文子串的最右端点位置,id为这个回文子串的中心点位置,那么len[id] = mx- id + 1。
(1)当i <= mx
此时i在以id为中心的回文串,假设i相对于中心点id的对称点为j,len[j]已经计算过了。
假设len[j] < mx - i,即如下图所示
此时说明以j为中心的回文串一定在以id为中心的回文串内部,且i和j关于id对称,由回文串的定义可知,一个回文串反过来仍然是回文串,所以以i为中心的回文串长度至少和以j为中心的回文串长度相等,即len[i] >= len[j],因为len[j] < mx - i,所以i + len[j] < mx,
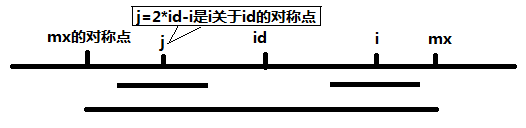
假设len[j] >= mx - i,如下图所示
由于回文的对称性,说明以i为中心的回文串可能延伸到mx之外,而大于mx的部分的字符还没有进行匹配比较,所以要从mx+1位置开始一个一个字符匹配知道失配,匹配完成后及时更新mx和对应的id以及len[i]。
(2)当i >= mx
由于i比mx还大,说明对于中心点为i的回文串还没有计算过,这个时候只能左右展开一个个字符的匹配,匹配完成之后更新mx位置和对应的id以及len[i].
按照以上思路实现代码逻辑如下:
package cn.test.leetcode;
/**
* Created by GavinCee on 2019/5/1.
*/
public class PalindromicStr2 {
public static void main(String[] args) {
PalindromicStr2 palindromicStr = new PalindromicStr2();
String testStr1 = "babad";
String testStr2 = "cbbd";
String testStr3 = "gabbacg";
String testStr4 = "gabbac";
String testStr5 = "cabbac";
String testStr = "babadada";
System.out.println(palindromicStr.longestPalindrome(testStr));
System.out.println(palindromicStr.longestPalindrome(testStr1));
System.out.println(palindromicStr.longestPalindrome(testStr2));
System.out.println(palindromicStr.longestPalindrome(testStr3));
System.out.println(palindromicStr.longestPalindrome(testStr4));
System.out.println(palindromicStr.longestPalindrome(testStr5));
}
public String longestPalindrome(String s) {
if(s == null || s.length() < 1){
return "";
}
StringBuilder manacherStr = new StringBuilder("#");
for (int i = 0; i < s.length(); i++) {
manacherStr.append(s.charAt(i) + "#");
}
int[] len = new int[manacherStr.length()];
len[0] = 1;
int maxRightIndex = 0;
int index = 0;
int maxLength = len[0];
int maxIndex = 0;
for(int i = 1; i < manacherStr.length(); i++) {
if(maxRightIndex > i) {
int j = 2 * index - i;
if(len[j] < maxRightIndex - i) {
len[i] = len[j];
} else {
len[i] = maxRightIndex - i + 1;
//从maxRightIndex开始匹配,已经匹配了len[i]的长度了,所以左侧是i-len[i]
while (i - len[i] >= 0 && i+len[i] < manacherStr.length() && manacherStr.charAt(i - len[i]) == manacherStr.charAt(i+len[i])) {
len[i]++;
}
}
}else {
//此时还没有匹配
len[i] = 1;
while (i - len[i] >= 0 && i+len[i] < manacherStr.length() && manacherStr.charAt(i - len[i]) == manacherStr.charAt(i+len[i])) {
len[i] = len[i] + 1;
}
}
if(len[i] + i - 1> maxRightIndex) {
maxRightIndex = len[i] + i - 1;
index = i;
}
if(len[i] > maxLength) {
maxLength = len[i];
maxIndex = i;
}
}
//所以最大回文长度就是len[] - 1;
String resTmp = manacherStr.substring(maxIndex - maxLength + 1, maxIndex + maxLength -1);
return resTmp.replaceAll("#", "");
}
}
提交运行通过。